Kolesnikov.net

Алкуин (Alcuin, Ealhwine, Albinus, Flaccus)(ок.735 — 804) — учёный, богослов и поэт, друг, учитель и советник Карла Великого (748-814). Сочинения многочисленны: изданы Фробеном(2 тома, Регенсбург, 1777), письма: изданы Яффе в «Bibliotheca rerum germanicarum» (6 т. «Monumenta Alcuiana», Берлин, 1873). [Брокгауз и Эфрон,т.1.с.457-458]

В 1967г. в Университете Йорка (Великобритания) основан Alcuin College (Колледж Алкуина).

Статуя Алкуина находится на крыше Художественно-исторического музея в Вене (Kunsthistorisches Museum Wien, иногда Музей Истории Искусств). Штырь сверху - похоже молниеотвод. Вид со стороны музейного квартала (Museum Quartier). Фото автора 02.01.2018.

Расположение статуи Алкуина - четвертая справа.

Ласточка пригласила улитку на обед. Пройти улитке надо всего 1 лигу. Проблема в том, что улитка может проползти в день один только дюйм. Сколько дней и лет улитка будет ползти на этот обед?

Какими данными мы располагаем:
Лига - расстояние, которое человек проходит за 1 час. Ранее лига применялась в Европе и Латинской Америке.
В 1 лиге 1500 шагов, 1 шаг - 5 футов, 1 фут - 12 дюймов. Итого: 90000 дюймов.
Поскольку в день улитка проползает 1 дюйм, то ей понадобится 90000 дней или приблизительно 246 лет и 210 дней. Что и отмечено Алкуином.

Относительно данной задачи возникают три вопроса:
1) Сколько лет живут улитки?
Ответ на данный вопрос легко найти в Google: не двести лет, не сто и даже не пятьдесят.
2) Сколько дюймов в лиге?
Например, kalkulator.pro дает ответ 190 тыс. и тогда улитке потребуется 520 лет.
3) Как повлияют високосные годы?
В високосном году 366 дней. За некоторыми исключениями високосный год повторяется раз в четыре года. На 246 лет придется около 60 годов по 366 дней, и правильный ответ будет 246 лет и 150 дней. Високосные года были введены Цезарем в 45 году до н.э. задолго до появления Алкуина.

Рассмотрев эти три вопроса, мы видим, что постановка вопроса Алкуином имеет чисто теоретическое значение, поскольку улитка живет несколько лет и не сможет ползти ни сто, ни двести лет. На решение задачи сильно влияет количество дюймов в лиге, которое сложно определить точно, так как много воды утекло с тех пор, как Алкуин составил свои задачи. И третий вывод, наличие високосных годов влиет на общий ответ незначительно, хотя сам по себе срок в два месяца/60 дней незначительным не назовешь.

Шел себе человек по улице и вдруг увидел группу людей. Он не нашел ничего лучшего, чтобы сказать: вас так много, что если число вас удвоить, к нему добавить половину, потом еще половину, а также сосчитать и меня, то получится 100. Кто готов сказать, сколько народа на улице?

Алкуин говорит: 36. А дальше проверяет решение. Теперь такие задачи принято решать с помощью уравнения, например, вот такого:

2x + x/2 + x/4 + 1 = 100, тогда x = 36.

Два человека спокойно шли себе по улице и вдруг увидели аистов. «Сколько их здесь?» - спросили они друг друга. Предположим, сказал один, если число аистов удвоить, к ним еще раз добавить число аистов (некоторые эту операцию называют утроением), затем добавить половину трети этой суммы, и наконец, добавить просто двух аистов, то получим число 100. Ну и сколько аистов там было?

Составляем уравнение:
3x+3x/(2*3)+2 = 100
7/2 x = 98
x = (98/7)*2, получаем x = 28.
98 можно разделить на семь не прибегая к калькулятору: 98 = 70 + 28, семьдесят дают 10, а 28 - 4. Итого 14. Удваиваем, получаем 28.

Увидел человек как-то лошадей, пасущихся в поле, и подумалось ему: «Я хочу, чтобы эти лошади стали моими». Но человек был не прост. Он сначала решил посчитать лошадей. Как и в предыдущих задачах весьма странным способом. Он заметил, что если число пасущихся лошадей удвоить, а затем к этой сумме добавить половину половину (два раза по половине) этой суммы, то получится 100. Вопрос: на сколько лошадей мог претендовать этот наглый человек?

Человек сказал: «Я хочу купить 100 свиней за 100 динариев». Известно, что боров стоит 10 динариев, матка свиньи - 5 динариев, а два поросенка идут по 1 динарию. Сколько боровов, маток и поросят можно купить на этих условиях?

Мы просто составим два уравнения:
x1 + x2 + x3 = 100
10x1 + 5x2 + 0.5*x3 = 100

На 100 динариев можно купить или 10 боровов, или 20 маток или 200 поросят. Если купим 100 поросят, то останется 50 динариев, что хватит на 10 маток. 90 поросят - останется 55 динариев, их хватит на 9 маток и одного борова. Итого: 90 поросят, 9 маток, 1 боров.

Два фермера имели вместе 100 динариев, на которые они хотели купить свиней. И купили несколько групп по пять свиней по 2 динария за группу. Далее они хотели откормить этих свиней и продать с прибылью. Но тут до них дошло, что не время зимой откармливать свиней и держать их на ферме тоже толку мало. Они решили продать их с прибылью немедленно. Но не тут-то было. Потому что покупатели были готовы купить их свиней за те же деньги: два динария за пятерых (от себя добавим, что им еще повезло). Они подумали и решили: надо поделить свиней. Тогда они смогут их продать и еще получить прибыль. Как им это удалось?

Они должны продать 250 свиней. Один фермер взял 125 отличных свиней, а другому осталось 125 свиней (что осталось, то осталось). Первый продал 120 по динарию за 2, а второй - 120 по динарию за 3. Так они свои 100 динариев и набрали. А по пять свиней у каждого остались в качестве прибыли. С математикой в данной задаче не очень, а с точки зрения реальной жизни вполне практичный ход: скупать группами, делить, сортировать и продавать.

Тарелка весит 30 фунтов или 600 шиллингов. Сделана она из сплава золота, серебра, меди и олова. В ней серебра больше чем золота в три раза. (Конечно). Меди больше чем серебра тоже в три раза. А олова в три раза больше, чем меди. Сколько весит каждый метал?

Ну здесь все просто: суммируем по частям, общий вес известен.

Золото весит 15 шиллингов, серебро, соответственно, 45, медь 135, а олово - 405. (перед 405 стоит тире, а не знак минус).

Бочка заполнена 7200 пинт воды. Третья часть плюс шестая - вытекает через первую трещину. Третья часть вытекает через вторую трещину. Через третью трещину вытекает шестая часть. Сколько вытекает через каждую трещину?

Можно заметить, что через первую трещину вытекает столько же, сколько через вторую и третью. Впрочем можно этого не замечать, а решать задачу в общем виде. Но раз уж мы заметили, то через вторую и третью трещину вытекает 3200 пинт, причем через вторую - третья часть от половины, т.е. 2/3 или 2400 пинт.

На долю третьей останется 1200 пинт. А через первую вытекает столько же, сколько через вторую и третью, а именно 3600 пинт. 

Ответ: Первая трещина 3600 пинт, вторая - 2400, третья - 1200. Итого 7200.

Имеется материал длиной 100 футов и шириной 80. Сколько мантий можно нарезать из этого материала, если мантия имеет в длину 5 футов, а в ширину 4?

Из 100 футов длины можно вырезать 20 мантий длиной 5 футов, а из 80 футов ширины можно вырезать 20 мантий шириной 4 фута. Итого материала хватит на 400 мантий. Если мантии повернуть, то из длины в 100 футов можно нарезать 25 мантий по 4 фута, а из ширины в 80 футов - 16 мантий по 5 футов. Итого всего 400. Ответ остался тем же, но это просто цифры удачно подобраны.

Имеется отрез ткани 60 футов в длину и 40 в ширину. Необходимо нарезать эту ткань на маленькие отрезки по 6 футов в длину и 4 в ширину. Одного такого отрезка как раз хватает на тунику. Сколько туник можно сделать из первоначального отреза?

10 в длину и 10 в ширину, итого 100. А вот если резать в другом направлении, то получится так: 15 с одной стороны и 6 с другой, итого 90. Останется отрезок шириной 4 и длиной 60, здесь поместится 10 туник, так что результат будет тот же - 100.

11. Задача о двух мужчинах, женившихся на сестрах.

Теми же, что и без сестер - кузенами (двоюродными братьями), только с сестрами они будут кузенами дважды.

Означенный отец умер и оставил своим трем сыновьям 30 стеклянных сосудов, из 10 были полны вином, 10 - заполнены вином наполовину, а 10 - пусты. Разделите вино и сосуды так, чтобы каждому из сыновей всего досталось поровну.

Каждому должно достаться 10 сосудов, из них пять полных вина. Самое простое решение: одному сыну выдать десять полуполных сосудов, а 10 полных сосудов разделить между оставшимися сыновьями. Пустые десять разделить между ними тоже.

Если поделить все тупо поровну, то каждому достанутся по 3 сосуда: полных, полупустых и пустых. И останутся неразделенными: полный сосуд, полупустой и пустой. Тут надо или переливать полный в пустой, чтобы получить три полупустых, или одному сыну выдать полупустой, а дальше производить сложный обмен: одному выдать полный и пустой, а взамен у него забрать полупустой и отдать оставшемуся сыну.

Король решил собрать армию и приказал слуге идти в тридцать деревень. Пришел слуга в первую и ушел с одним бойцом. Пошли они с бойцом в две другие деревни и стало их четверо. Эти четверо пошли в другие четыре деревни и т.д. Сколько людей может быть собрано с 30 деревень?

Типичная задача на удвоение, которую уже в 20 веке рассматривал Перельман Я.И. После 10 деревни 1024 бойца пошли в очередные деревни. После 15-й деревни 2**15 это составляет около 512 тыс. человек. Здесь Алкуин стыдливо ставит «и т.д.». Его английские переводчики {John Hadley and David Singmaster } доводят дело до абсурдного конца 2**30 = 1 073 741 824 попутно замечая, что таких деревень не было и нет. Эта задача показывает, что во времена Алкуина числа вроде миллиарда не вызывали проблем.

Сколько следов на последней борозде оставит вол, на котором пахали весь день.

Алкуин показывает, что ему не чужды отвлекающие задачи. Пашущий вол не оставляет следов, поскольку за ним движется плуг и затирает все следы.

Сколько борозд на поле, если пахарь должен сделать три разворота на каждом конце поля.

Первая борозда поворота не требует. На каждый поворот 2 борозды. Итого 7. На рисунке все четко видно. (Рисунок не Алкуина).

Двое мужчин вели волов по дороге и сказал один другому: «передай мне двух волов и у меня будет столько же волов, как и у тебя». Другой отвечает: «Ежели после этого ты мне передашь двух волов, то у меня их станет вдвое больше». И сколько же волов было у каждого собеседника?

С помощью уравнений, которых Алкуин не знал. Пусть x - число волов у первого собеседника, а y - у второго.
х + 2 = y - 2
2 (x + 2- 2) = y - 2 + 2 ; 2x = y
Получаем из первого уравнения y = x + 4, подставляем во второе:
2x = x + 4
x = 4; а y = 8.
Алкуин говорит точно то же, а потом и проверяет ответы методом подстановки.

Три брата подошли к реке. Каждый брат был с сестрой. На берегу нашлась только маленькая лодка на двух человек. Как им всем переправиться, если нельзя никакую сестру оставить наедине с незнакомым мужчиной? С братом - можно.

Мужчина с сестрой пересекает реку, оставляет сестру и возвращается. Выходит и следующий мужчина с сестрой пересекает реку, высаживает сестру и возвращается. Третий мужчина берет свою сестру, переправляет ее и возвращается. Все сестры переехали, остались три мужика на первоначальном берегу. Один из братьев может переправить их по очереди. Ничего сложного. Посчитаем количество рейсов: три на перевозку сестер и два оставшихся мужчин. Итого пять туда и обратно. (последний без обратно).

Перевозчик должен перевести волка, козу и капусту, но в лодку влезает только две позиции из трех. Как ему перевезти их всех, если волк хочет съесть козу, а коза - капусту и их вместе наедине оставить никак нельзя?

Перевозчик везет козу, а волка оставляет наедине с капустой. Возвращается и забирает волка. Привозит волка к козе, но козу забирает обратно. Снова берет капусту, а козу оставляет. Пусть волк развлекается с капустой. Напоследок возвращается и забирает бедную овечку, козу то есть. 

Это самая знаменитая из задач Алкуина. Дополнительную инфорацию по ней, а также альтернативный способ решения, можно почерпнуть на:
http://suhin.narod.ru/mat4.htm

Муж с женой, каждый из которых весил как груженая телега, имели двух детей, каждый из которых весил как половина телеги. Им понадобилось пересечь реку, но лодка могла выдержать только одну телегу. (Телега здесь виртуальная и ее переправлять не надо). Найти для них всех возможность переправиться и не утонуть.

Так дети могут по одному плыть на лодке, то сначала дети переплывают реку. Потом один возвращается и плывет уже их мать. Она остается на другом берегу, а второй ребенок возвращается и перевозит на другой берег первого ребенка. Теперь один из детей может сплавать обратно и передать лодку отцу. Отец переплывает реку и возвращает лодку со вторым ребенком. Второй ребенок забирает первого и вот уже все на другом берегу.

Мужчина и женщина хотят переправиться через руку. Они увидели на берегу лодку с двумя детьми, да только лодка может взять или двоих детей или одного взрослого. Как можно переправить взрослых, да так, чтобы дети вернулись на первоначальный берег?

Аналогично предыдущей задаче. Сначала дети переплывают реку, потом один из них возвращается, отдает лодку женщине и она переплывает реку. Ребенок, оставшийся на той стороне реки, возвращает лодку и перевозит второго ребенка на новый берег. Потом возвращается и отдает лодку мужчине. Мужчина перебирается через реку и отдает лодку ребенку на том берегу. Ребенок перегоняет лодку и вот уже мужчина с женщиной переправились, а дети остались на первоначальном берегу.

Имеется поле 200 футов длины и 100 ширины. Я хочу разместить на этом поле овец так, чтобы каждая овца имела площадку пять футов длины и четыре ширины. Сколько овец можно разместить на таком поле?

Такое же, как при делении ткани в задачах, приведенных ранее. В длину можно разместить 200/5=40 участков, в ширину 100/4 = 25. Итого 40*25 = 1000 овец. Или иначе 200/4 = 50 и 100/5 = 20, итого 50*20 = 1000. Результат тот же.

Такие квадратные поля, как в предыдущей задаче, все-таки встречаются не всегда. Теперь поле имеет 100 футов по каждой стороне, 50 футов по одному фронту, 60 - в середине и 50 футов по другому фронту. Сколько квадратных футов составляет площадь этого поля?

Вашему вниманию предлагается поле, одна сторона которого 30 ярдов, другая 32, третья 34, а четвертая снова 30. Сколько квадратных ярдов в таком поле?

Формула Герона для площади четырехугольника:

Это поле имеет 30 ярдов в длину по одной стороне, 30 - по другой, и 18 - по фронту. Какова площадь этого поля?

Круглое поле имеет 400 ярдов в окружности. Какова площадь этого поля.

Здесь все просто для нас, но не для Алкуина.
Радиус равен окружности разделить на 2π: итого 200/π.
Площадь πR**2 или 40000/π = 40000/3.14 = 12739.
Алкуин же использует значение π = 4 и получает 10000 кв. ярдов, что обладает несколько повышенной погрешностью.

Имеем поле длиной 150 футов. На одном конце поля стоит собака, а на другом заяц. Собака несется прыжками по 9 футов длиной, а заяц убегает прыжками по 7 футов. Причем прыжки зайца и собаки занимают одно время. (Не понятно почему, но важно для решения). Сколько футов пробежит собака и сколько она сделает прыжков, пока не схватит зайца?

Есть город одна сторона которого 1100 футов, другая - 1000 футов, фронтальная - 600 футов и четвертая сторона - 600 футов. Каждый дом имеет 40 футов длины и 30 футов ширины. Сколько домов можно разместить в городе.

Алкуин решает задачу через площадь и получает ответ 525 домов. Но поскольку форма города не правильная, разместить дома без остатков не получится.

В наличии треугольный город 100 футов на 100 футов и на 90 футов. Сколько можно построить домов длиной 20 футов и шириной 10?

Алкуин решает все через площадь и получает 20 домов. Как их можно разместить в треугольнике?

Длина окружности города 8000 футов. Сколько можно разместить домов 20 на 30 футов?

Базилика имеет в длину 240 футов и 120 футов в ширину. Она замощена плиткой 23 на 12 дюймов. Сколько было использовано плиток? В одном футе 12 дюймов.

В длину нужно 240*12/23 = 125.21. Взять нужно 126 плиток, потом лишнее отбить.
В ширину 120*12/12 = 120.
Итого: 126*120 = 15120.

Попробуем положить плитку поперек.
Тогда 240*12/12 = 240
120*12/23 = 62.6 или 63.
Все равно 240*63 = 15120.

Винный погреб имеет 100 футов в длину и 64 в ширину. Сколько бочонков вместится в данный погреб, если длина бочонка 7 футов, ширина 4 (странные бочонки какие-то), а посередине надо оставить проход в 4 фута шириной.

Алкуин говорит 210.
Грубая оценка максимального значения, исходя из площади 100*60/(7*4) = 214.2
Если мы ровно посередине оставим проход, то получим два помещения 100*30.
Разместим 7 по длинной стороне, 4 по короткой. Получим 14*7 = 98. Общее количество не дотягивает до 200.
Разместим 7 по короткой стороне, 4 по длинной. 4*25 = 100 бочонков. Уже лучше. Теперь двести.

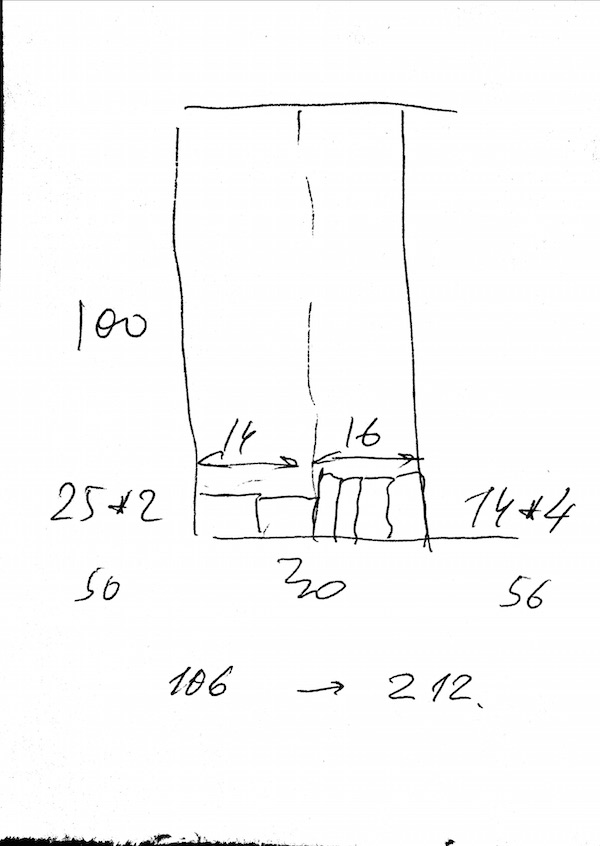
Теперь разделим помещение 100*30 на два 100*14 и на 100*16.
В первом разместим бочонки поперек: 2 по 7. Всего поместится 25 бочонков (100/4).
Во втором вдоль: 4 по 4. В длину поместится 16 рядов, итого 56 бочонков.
Всего в погреб можно поместить (50+56)*2 = 212.
Ура! Мы превзошли Алкуина.

O'Connor and Robertson, www-history.mcs.st-andrews.ac.uk/HistTopics/Alcuin_book.html вообще предлагают проход чуть сдвинуть и разместить 214 бочонков, что приближается к {мировому рекорду} максимально возможному случаю.

Глава семьи приказал 20 своим домочадцам взять 20 мер кукурузы, причем мужчина должен был взять 3 меры, женщина - 2, а ребенок полмеры. Сколько мужчин, женщин и детей было в хозяйстве?

Пусть x, y, z - количество мужчин, женщин, детей.
x + y + z = 20
3x + 2y + 0.5z = 20
Второе уравнение можно умножить на 2:
6x +4y + z = 40
Из него можно вычесть первое:
5x + 3y = 20
В данном уравнении x может быть равен 0, 1, 2, 3, 4.
x = 0; y = 20/3
x = 1; y = 5
x = 2; y = 3.333
x = 3; y = 2/3
x = 4; y = 0
Второй и третий ответы требуют дробного количества женщин, физический смысл в этом случае отсутствует. Четвертый ответ требует 0 женщин, что вполне может означать их отсутствие.
x = 1; y = 5; z = 14
x =4; y = 0; z = 16
Ответ с четырьмя мужчинами кривоват в бытовом смысле, но вполне соответствует условиям задачи.

Алкуин уравнений не использует, а просто дает ответ и потом проверяет его правильность. В данном случае это 1 мужчина, 5 женщин и 14 детей.

33. Задача о другом главе семьи, продающей зерно.

Глава семьи приказал 30 своим домочадцам взять 30 мер кукурузы, причем мужчина должен был взять 3 меры, женщина - 2, а ребенок полмеры. Сколько мужчин, женщин и детей было в хозяйстве?

x + y + z = 30
3x +2y +0.5z = 30
или
6x + 4y +z = 60

Вычтем из второго первое и получим:

5x +3y = 30

x = 0, 1, 2, 3, 4, 5, 6, поскольку дробного числа мужчин быть не может.
x = 0; y = 10
x = 1; y = 25/3
x = 2; y = 20/3
x = 3; y = 5
x = 4; y = 3.33
x = 5; y = 5/3
x = 6; y = 0
Дробного числа женщин не бывает. Устаивает вариант с тремя мужчинами и 5 женщинами. Детей при этом 22 из первого уравнения. Два других варианта без мужчин или без женщин тоже реальны.

34. Еще одна задача про распределение зерна.

Зерно делится теперь на 100 домочадцев. Соотношение то же: мужчинам 3 меры, женщинам - 2, детям половину.

11 мужчин, 15 женщин и 74 ребенка. Вообщем, есть еще ряд тоже правильных ответов.

Умер владелец состояния в 960 фунтов и оставил беременной жене завещание: если родится сын, то он должен получить 3/4 наследства. Жена, соответственно, 1/4. Если дочь, то 7/12 от наследства, а жена - 5/12. Но жена родила двойню: мальчика и девочку. Сколько наследства получит каждый?

Алкуин почему-то делит наследство пополам, а потом высчитывает доли матери и сына и дочери в каждой половине.
Мать получит: 1/2 * 1/4 + 1/2 * 5/12 = 8/24 = 1/3; итого 320 фунтов.
Сын: 1/2 * 3/4 = 3/8; всего 320 фунтов.
Дочь: 1/2 * 7/12 = 7/24; всего 280 фунтов.

Старик приветствовал мальчика словами: «Живи так долго, как ты уже жил, и еще столько, и умножить это на 3. А если бог даст тебе еще год, то проживешь ты сто лет». Сколько лет мальчику сейчас?

Человек захотел построить дом и нанял шесть рабочих. Пять из них были мастерами, а один подмастерьем. В день платилось 25 фунтов. Сколько получили мастера и подмастерье, если оплата подмастерья в два раза меньше оплаты мастера.

38. Задача о человеке, купившем 100 животных.

Купил кто-то как-то 100 различных животных за 100 фунтов. Лошадь стоила 3 фунта, корова - 1, а овец на 1 фунт можно было купить 24. Сколько лошадей, коров и овец было закуплено?

Чтобы отправиться в путешествие на Восток, купец купил 100 различных животных за 100 фунтов. Он заплатил 5 фунтов за каждого верблюда, по 1 фунту за осла и на один фунт покупал 20 овец. Сколько верблюдов, ослов и овец он купил?

Одна свинья родила в центре города семирых поросят. Все пороси в данной задаче девочки. Все потомки и их мать родили по семь поросят в первом углу города. Потом все собрались, перешли во второй угол города и родили по 7 поросят. Потом также перешли в третий и четвертый углы и все родили по 7 поросят. Потом все собрались вместе и перешли в центр города. Здесь тоже родили по 7 поросят. Сколько всего свиней образовалось в этот момент в городе.

Есть лестница с сотней ступенек. На первую ступеньку сел один голубь, на вторую - два, на третью - три и так далее до ста. Сколько всего голубей уселось на лестнице?

Было у хозяина 300 поросят. Он приказал забить их в три дня, только не знал, сколько было забито в каждый день конкретно. Потом он попросил сделать то же самое с 30 поросятами. Да еще захотел, чтобы в каждый день забивалось только нечетное количество поросят. Сколько поросят забивали каждый день?

44. Задача о мальчике, приветствующем его отца.

«Здравствуй, отец», - сказал мальчик. «Здравствуй, сын мой», - ответил отец. «Если ты проживешь дважды свой нынешний возраст, а затем полученный возраст еще трижды, а потом добавишь еще один год, то станет тебе сто лет». (Интересное такое приветствие отца). Сколько лет сейчас сыну?

Голубь сидел на дереве. Он увидел других голубей, летящих рядом, и сказал: «Допустим, добавим столько голубей, сколько вас тут, и еще столько. А если добавить меня, то будет сто голубей». Сколько голубей прилетело?

Человек шел по улице и нашел сумку с двумя талантами. Толпа на улице заметила это и сказала: «Дружище, поделись с нами». «Нет» - был его ответ. Тогда толпа набросилась на него и отобрала сумку. Толпа честно поделила награбленное: каждому досталось 50 золотых шиллингов. Более того, у ограбленного тоже осталось 50 золотых шиллингов. Сколько человек было в толпе, случайно проходившей мимо человека, нашедшего кошелек?

Епископ заказал 12 буханок хлеба, чтобы поделить их среди священнослужителей. Он определил, что священники получат по две буханки, дьяконы - по половине, а чтецы - по четверти. Так уж получилось, что число людей, получивших буханки по вышеприведенным принципам, и число буханок совпало. Сколько всего было священников, дьяконов и чтецов?

48. Задача о человеке, встретившем учеников.

Человек встретил группу учеников и спросил: «Сколько вас всего в вашей школе?» Вместо того, чтобы просто сказать число, один из учеников заметил: «Мне бы не хотелось говорить об этом прямо, но если ты возьмешь число учеников, потом удвоишь это число, а затем результат еще и утроишь, полученное разделишь на 4 группы и меня добавишь в одну из них, то результатом будет 100». Так сколько же учеников в сей математической школе?

Семь плотников сделали каждый по семь колес. Сколько тележек они могут построить?

Я задам следующий вопрос, на который любой может ответить. Сколько пинт в 100 мерах вина и сколько чашек в 100 мерах вина.

51. Задача о человеке, делящем бочонок вина.

Решил человек поделить наследство между своими четырьмя сыновьями. Было у него четыре бочонка вина: в одном 40 мер, в другом - 30, в третьем - 20, а в четвертом - 10. Он позвал слугу и сказал разделить все вино поровну. Никакой дополнительной посуды у слуги не было.

Глава семьи приказал привезти 90 мер зерна из отдаленного хранилища. До хранилища - 30 лиг. Перевезти может верблюд. Ему потребуются три ходки. Когда он несет груз, то съедает за одну лигу по 1 мере зерна. Сколько зерна останется после перевозки верблюдом?

Настоятель решил раздать 204 яйца своим 12 монахам всем поровну. Из них 5 священников, 4 дьякона и 3 чтеца. Сколько яиц досталось священникам, сколько дьяконам и сколько чтецам?

John Hadley and David Singmaster The Mathematical Gazette Vol. 76, No. 475, The Use of the History of Mathematics in the Teaching of Mathematics (Mar., 1992), pp. 102-126 http://www.jstor.org/stable/3620384

Сухин И.Г. Задача “Волк, коза и капуста”. Удивительные находки и неразгаданные загадки.// НАЧАЛЬНАЯ ШКОЛА №7-2002, c. 69-70.
http://suhin.narod.ru/mat4.htm

Более ранние редакции:
23.06.2017
30.05.2017
19.03.2017
04.03.2017
27.02.2017
27.07.2016

Алкуин. 53 задачи для развития молодых умов.