Задачи Ферми.

Это здесь. Версия от 06.05.2023 22:12

Другая версия: Botan.us

Kolesnikov.net

Задачи Ферми и другие способы обсчитать этот мир...

Движение по Web-страничке: Mac: Command+стрелка вверх (в начало), Command+стрелка вниз (в конец), Пробел (вниз на экран), Верхний регистр+Пробел (вверх на экран)

ОБСЧИТАТЬ, обсчитаю, обсчитаешь, совер. (к обсчитывать), кого что.
1. Неверно сосчитав, дать кому нибудь меньше (денег). «Обсчитал, воровская душа!» Некрасов.
2. Произвести подсчет чего-нибудь (спец.).

[Толковый словарь Ушакова. Д.Н. Ушаков. 1935]
https://ushakovdictionary.ru/word.php?wordid=38535

§1.

Как быстро посчитать овец.

Два джентльмена едут в поезде. За окнами появляется стадо овец.
- Интересно, сколько их, - говорит один.
- Триста восемьдесят четыре, - отвечает другой.
- ?? Как вам удалось так быстро подсчитать?
- О, это очень просто. Надо только сосчитать количество ног и разделить на четыре.
[Народное творчество]

{Сколько всего было ног? (Быстро и без калькулятора!)}

§2.

На отметке 10:04 в фильме «Кавказская пленница» можно отметить такие слова, сказанные продавцом шашлыков «колоритным стариком-горцем»:

— …и принцесса от злости повесилась на собственной косе, потому что чужестранец совершенно точно сосчитал, сколько зерен в мешке, сколько капель в море и сколько звезд на небе.
Так выпьем же за кибернетику!

Кавказская пленница. Сценарий.
https://kinodramaturg.ru/kavkazskaya_plennica_scenariy/2

Полная история выглядит так:
(С кавказским акцентом)

Адин бэдний юноша влюбился в принцессу, и решил попросить её руки. Но она рассмеялась ему в лицо и сказала, что станет женой того, кто виполнит любые три её желания. Юноша согласился.
И принцесса от злости повесилась на собственной косе, потому, что он совершенно точно сосчитал сколько зёрен в мешке, сколько капель в море, и сколько звёзд на небе.
Так випьем же за кибернетикэв!
http://vodka.kiev.ua/vodka-and-feast/toast/tost-24

{История из "Кавказской пленницы" подсказана Золотухиным В.Л.}

§3.

"Вот, - сказал он, - три вопроса:
Разрешишь - возьму в пажи!
Много ль капель в синем море?
Посчитай-ка да скажи!"

"Я сочту, - ответил мальчик, -
Счет не долог, не тяжел,
Но, пока считать я буду,
Повели, чтоб дождь не шел".

"Ну а много ль звезд на небе?"
И философ, не смутясь:
"Повели сойти им с неба,
Я тогда сочту как раз".

Майков Апполон Николаевич (1821-1897) Восходит к сказкам братьев Гримм. Цит. по
http://maykov.lit-info.ru/maykov/stihi/stih-370.htm

Первый раз встретилось в
[Святловский1933p5-6].
Первая фраза там звучит несколько иначе:
"Вот, - сказал король, - вопросы..."

{К сожалению, пожелания мальчика нереальны: Дождь идти не перестанет. Звезды с неба не сойдут. А капли и звезды считать надо…
В своем стихотворении Майков А.Н. поднимает проблему снятия параметров в динамических системах.}

§4.

Сколько настройщиков пианино в Чикаго?

Как ничего не зная о предмете и обладая только общими знаниями, здравым смыслом и определенной долей наглости, определить, хотя бы приблизительно, с точностью до порядка, какую-либо величину. Или поймать оппонента, если величина не лезет ни в какие рамки. Или просто удивить окружаюших.

Далее вы оттачиваете методику решения таких задач, набираетесь опыта и знаний, и ваши расчеты становятся гораздо точнее.

Такие задачи принято называть задачами Ферми по имени итальянского физика Энрико Ферми (1901-1954), лауреата Нобелевской премии 1938г. (НПФ-1938), который в 1939г. эмигрировал в США и стал одним из основных разработчиков первой атомной бомбы. ("Проект Манхэттен» (Manhattan Project)).

Wikipedia: https://ru.wikipedia.org/wiki/Ферми,_Энрико

Ферми любил задавать подобные задачи на своих лекциях, и считал, что человек с дипломом физика, должен уметь решать такие задачи быстро и четко.

В задачах Ферми не хватает данных. Их просто нет. Их надо найти. Их надо взять из окружающего мира, из справочника, из опыта.

Задачи Ферми требуют знания фактов, которые не входят в формулировку задачи, отмечает [Baeyer1993p6].

Ответ тоже будет не вполне точный. Но он должен соответствовать приблизительно и давать понимание сущности процесса.

Пример поиска в Google:
https://www.google.com/search?q=Задачи+Ферми
https://www.google.com/search?q=Fermi+problems

Можно выделить три направления применения задач Ферми:
Это подбор кадров, способных решать данные задачи.
Это проверка информации на соответствие: может ли такое быть. Заметить какую-либо неточность иногда бывает очень полезно.
Это обучение школьников и студентов правильным методам мышления.

Также отметим, что Ферми был иностранным членом-корреспондентом Академии Наук СССР с 31.01.1929г. Также он был иностранным членом Академии Наук СССР. Информация об этом содержится на сайте Академии Наук, но дата не указана.
http://www.ras.ru/win/db/show_per.asp?P=.id-52497.ln-ru.dl-.pr-inf.uk-12

Фотография Энрико Ферми с пропуска в Лос-Аламосе.
Другие красивые фотографии Э.Ферми, в том числе и эту, можно найти в Википедии по адресу:
http://ru.wikipedia.org/wiki/Ферми,_Энрико,
а также в английской и итальянской версиях. Там же можно найти образец подписи Э.Ферми.

Русский термин "задачи Ферми" имеет несколько похожих переводов на английский язык:

Fermi problem,
Fermi quiz,
Fermi question,
Fermi estimate,
Fermi flexes [Angier2009],
guesstimation,
order estimation,
back-of-the-envelope calculation.

Также в русском языке применяется термин "задачи-оценки" со схожим значением.

Общие понятия для задач Ферми:

[2] : http://ru.wikipedia.org/wiki/Ферми,_Энрико

[3] : https://en.wikipedia.org/wiki/Fermi_problem

[4] : https://en.wikipedia.org/wiki/Back-of-the-envelope_calculation

Автор впервые столкнулся с задачами Ферми в книге Хаббарда Д.: Как измерить все, что угодно [Хаббард2009]. Две задачи: определение мощности взрыва при помощи разбрасывания листочков бумаги и определение количества настройщиков пианино в Чикаго, показались очень интересными и привлекли внимание к данному вопросу. Автор постарался собрать всю информацию по задачам такого типа, которую смог обнаружить.

Самая первая задача Ферми связана с его прибытием в США. 10 декабря 1938г. Ферми присутствовал на вручении Нобелевской премии в Стокгольме, 24 декабря он отплыл из английского порта Southhampton по направлению к Америке. 2 января 1939г. лайнер Franconia прибыл в Нью-Йорк. Существует легенда, что американские иммиграционные власти предложили новоиспеченному нобелевскому лауреату пройти тест на способности (aptitude test). Его попросили сложить 15 и 27 и разделить 29 на 2… Это Вам не считать настройщиков пианино. Но, судя по тому, что в итоге американское гражданство он получил, данный тест Ферми прошел успешно. Легенда подтверждается воспоминаниями дочери Ферми. [Barbour1995, Кикоин2011p81, Schwartz2017p143_145_149, Fermi1939].

§5.

В свое время Айзек Азимов написал фантастический рассказ, в котором талантливый техник открыл, что для выполнения арифметических действий не обязательно прибегать к калькулятору. Достаточно карандаша и бумаги. Рассказ называется "Чувство силы" (The Feeling of Power) [Азимов1958].

[5] Азимов1958: Азимов Айзек (Isaac Asimov) (1920-1992): Чувство силы [= Сколько будет 9х7].
www.lib.ru/FOUNDATION/feelpowr.txt
Ориг. назв.: Isaac Asimov. The Feeling of Power. 1958.

Айзек Азимов (Isaac Asimov) (1920-1992)
https://ru.wikipedia.org/wiki/Азимов,_Айзек

§6.

Известен ряд задач (вопросов) Ферми, которые он задавал своим студентам. Самым известным является задание:

#2 Сколько настройщиков пианино в Чикаго?
[Morrison1963p627]

Несмотря на то, что, кажется, данных о задаче совсем нет, это не так. Известна численность населения Чикаго во времена Ферми - это три миллиона человек. Известно среднее число человек в семье - это два или три человека. (Имеем миллион семей) Процент семей, имеющих пианино и пользующихся услугами настройщиков - от 3 до 10. Это самые тонкие и сложно определяемые цифры.  Возьмем 5%. (50000 настроек) Дальше - проще: берется частота настройки, скажем, раз в год, количество настроек в день и число рабочих дней в году. Настройка четырех инструментов в день при 250 рабочих днях в году (всего 365 минус 52 воскресенья, 52 субботы, несколько дней праздников) даст 1000 настроек в год и необходимость наличия 50 настройщиков. Что Ферми и проверял по "Желтым страницам" (или их аналогу). Конечно, количество пианино, требующих настройки (процент семей), определено очень приблизительно и, если подставлять границы интервала, результат получит большой разброс (от 30 до 100). Но это лучше, чем ничего, и позволит оценить порядок величины количества настройщиков.

Прошло 60-70 лет и население Чикаго оказалось равно 9 млн. чел.

А может можно узнать население города по количеству настройщиков пианино, взятому из Желтых страниц?

Ниже приведен неполный список работ, где рассматриваются настройщики пианино:
Morrison1963p627 (Только упоминается: How many piano tuners are there in the city of Chicago?)
Adam1995p21

10. Estimate the number P of piano tuners in a certain city or region.
Оцените число настройщиков пианино в определенном городе или регионе.
Рассмотрите население региона N со средним количеством пианино p в семье (в общем p<1). Допустим пианино настраивается b раз в год (в общем мы ожидаем 0=<b<2). Тогда число настроек в год равно:
Npb/n₁, где n₁ - средний размер домохозяйства (количество человек в семье).
Если каждый настройщик настроит n₂ пианино в день (причем n₂, больше 0 и меньше 4), что составит 250n₂ пианино в год. Таким образом, число настройщиков пианино в регионе (городе, поселке, деревне) приблизительно равно:
Npb/(250n₁n₂).
Подставим в эту формулу числа:
Для города Нью-Йорка:
N = 10⁷;
n₁=5;
b=0.5;
p=0.2;
n₂=2;
P = 10^{7 .}0.2 ^.0.5/(250 ^.5 ^.2) = 400,
что составляет порядок от 10² до 10³.

Nasa.gov:
https://www.grc.nasa.gov/WWW/k-12/Numbers/Math/Mathematical_Thinking/fermis_piano_tuner.htm

Если не открывется, то можно попробовать здесь:
http://web.archive.org/web/20170415081652/ https://www.grc.nasa.gov/www/k-12/Numbers/Math/Mathematical_Thinking/fermis_piano_tuner.htm

Примерно таким же методом как Ферми считал настройщиков пианино в Чикаго, Санджой Махаджан считал водителей такси в Бостоне [Mahajan2014p76]. И так же как Ферми проверял это количество: Ферми по Желтым страницам, а Махаджан по количеству медальонов, выданных властями Бостона. К этому вопросу близка задача из [Хаббард2009p11-12] по определению емкости рынка страховок. Он называет ее "Вопросы Ферми для нового предприятия".

Кузнецов А.П. оценивает количество кошек и домашних телефонов в Саратове (кошки отдельно и телефоны отдельно тоже):

Давайте оценим число домашних кошек в Саратове. В Саратове порядка 10⁶ человек. В каждой семье около 4 - 5 человек. Значит, в Саратове порядка 2x10⁵ семей. Зная сколько человек, сидит в классе, можно быстро подсчитать долю семей, в которых есть кошки. Это число колеблется от 1/4 до 1/2. Таким образом, в Саратове около 5x10⁴ – 10⁵ домашних кошек. Точно также можно оценить число домашних собак, телефонов и т.д. Оценки можно делать из разных соображений, здесь важен не столько путь решения, сколько результат. Например, число домашних телефонов можно оценить так. Я видел телефонные справочники, это две книги по 300 - 400 страниц. На каждой странице около сотни телефонов. Значит, число домашних телефонов, зарегистрированных на момент создания справочника, порядка 80 тысяч. [Кузнецов2006p12]

Гранинский герой считал количество жителей, разбуженных его мотоциклом. Гранин приводит ответ (семьдесят тысяч), но метод, которым было получено это число, остается за кадром. В отличие от него, герой Энди Вейера (Марсианин), тщательно подсчитывает свои запасы, на сколько дней хватит воздуха. И мы можем поучиться у него манере считать.

{Гранин Д. Иду на грозу. Собрание сочинений. Том 2. - СПб: Вита Нова, 2009, с.131
Вейер, Энди: Марсианин. [Фантастический роман]. - Пер. с англ. К.Егоровой. - М.: АСТ, 2014. - 382с. Andy Weir: The Martian. - New York: Broadway Books, 2004. - 387p. (first edition 2011, self-published).}

Герой романа братьев Вайнеров «Умножающий печаль» приготовил ванну с шампанским для своей любимой. «Тридцать пять ящиков по двенадцать бутылок. Без отстоя пены — полное булькающее корыто…»

К задачам Ферми: Сколько надо бутылок, чтобы наполнить ванну шампанским? И каков объем обычной домашней ванны?

Известный астрофизик Иосиф Шкловский рассказывал, как он в 70-х годах ХХ века раскрыл государственную тайну: определил число людей, сидевших в тюрьмах в Советском Союзе. Для этого ученый использовал старинный гершелевский «метод черпков», широко применяемый астрономами еще в XIX веке.
[Бондаров2016p418]

К сожалению автор не приводит ссылку, а прямой поиск по произведениям И.Шкловского "Вселенная.Жизнь.Разум" и "Эшелон" не позволил найти данный рассказ.

Метод звёздных подсчётов. Впервые применил Гершель У. ( Frederick William Herschel) (нем. Friedrich Wilhelm Herschel) (1738-1822)
https://ru.wikipedia.org/wiki/Метод_звёздных_подсчётов

§7.

Определение мощности ядерного взрыва. Метод Энрико Ферми.

История про клочки бумаги, бросаемые при прохождении ударной волны, стала визитной карточкой Ферми. Ниже вы можете увидеть кадр из фильма "Бесконечность" (Infinity, другое название на русском: "Бесконечная любовь". Реж. Мэттью Бродерик. 1996г. 119 мин.) Вообще-то фильм про Р.Фейнмана.

Друг Э.Ферми Э.Сегре, который на испытаниях был рядом с ним, пишет:

«Ферми встал и начал сыпать маленькие обрывки бумаги. Он подготовил простой эксперимент для измерения энергии взрыва: в спокойном воздухе обрывки бы упали к его ногам, а когда через несколько секунд после взрыва придет фронт ударной волны, они упадут несколькими сантиметрами (метрами?) дальше в направлении распространения ударной волны. По расстоянию до точки взрыва и смещению воздуха под воздействием ударной волны можно вычислить энергию взрыва. Эти вычисления Ферми проделал заранее, подготовив таблицу, по которой он мог сразу же определить энергию в результате такого грубого, но простого измерения… Этот случай настолько характерен для Ферми… Не менее характерно, что его ответ оказался очень близким к результату аккуратно проведенных официальных измерений. Но последний появился через несколько дней изучения записей, а Ферми получил свой через несколько секунд…» [Сегре1973p194]

Перед первым испытанием атомной бомбы 16 июня 1945г. на полигоне Тринити (штат Нью-Мексико) оценки ее мощности варьировались от 0 (если бомба не сработает) до 45000 тонн тротилового эквивалента.

Теллер поставил на 45 тыс. тонн, Ганс Бете - 8 тыс., Кистяковский - 1400, Оппенгеймер - 300. Норман Рамсей указал 0. Исидор Раби - 18 тыс. тонн. [Rhodes2012p656]

Ферми ставит вопрос иначе: "Не воспламенит ли бомба земную атмосферу? И если да, то сгорит при этом только американский штат Нью-Мексико или вся планета?" [Мания_История2012p331]

[6] Rhodes2012: Richard Rhodes The Making of the Atomic Bomb. The 25th Anniversary Edition. - New York: Simon & Schuster Paperback, 2012. - 838p.

Ферми пишет в своем отчете [Fermi1945] (Фотокопия отчета приведена ниже):

Утром 16 июля я занял позицию в базовом лагере на расстоянии около 10 миль от места взрыва. Взрыв был произведен около 5:30...Примерно через сорок секунд после взрыва взрывная волна настигла меня. Я попытался оценить мощность взрыва, бросая маленькие кусочки бумаги с высоты 6 футов до, во время и после прохождения взрывной волны. Так как в этот момент не было ветра, я смог четко измерить действительное перемещение кусочков бумаги во время их падения под действием взрывной волны. Их смещение составило около 2.5 метров, что должно было быть при взрыве по моей оценке 10 тысяч тонн тринитротолуола (ТНТ).

[7] Fermi1945: Fermi Е.: My Observations During the Explosion at Trinity on July 16, 1945// U.S. National Archives, Record Group 227, OSRD-S1 Committee, Box 82 folder 6, “Trinity.”

Расчеты с использованием более сложного оборудования, проведенные коллегами Ферми в течении нескольких дней, оценили мощность взрыва в 18.6 килотонн.

Критика метода Ферми не заставила себя ждать:

С двухметровой высоты Ферми бросает в воздух свои бумажные обрезки — до, во время и после прохождения ударных волн. Поскольку ветра в это время нет, то по дистанции между захваченными ударной волной бумажками и теми, что были брошены раньше, можно будет заключить о взрывной силе бомбы. Однако этот кустарный метод, похоже, следовало проработать лучше. Полученный результат в десять тысяч тонн тротила заметно отличается от полученных позднее, уточненных 18 600 тонн.
[Мания_История2012p342]

[8] Мания_История2012: Мания Х.: История Атомной бомбы.- Пер. с нем. Набатниковой. - М.: Текст, 2012. - 349с.

Остается вопрос: Как все-таки Ферми определил мощность взрыва? В общем, требуется оценить, какой метод использовал сам Ферми =:)
По-видимому, у Ферми была подготовлена таблица или простая формула с зависимостью мощности взрыва от дальности полета кусочков бумаги. Мы теперь знаем, что смещению на 2.5 м соответствовало 10 килотонн мощности взрыва. Что-нибудь вроде этого:

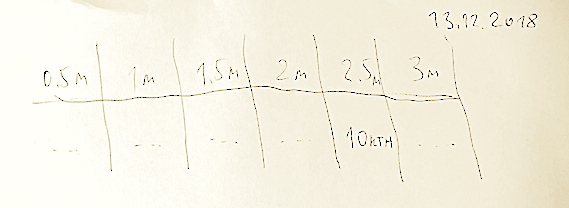
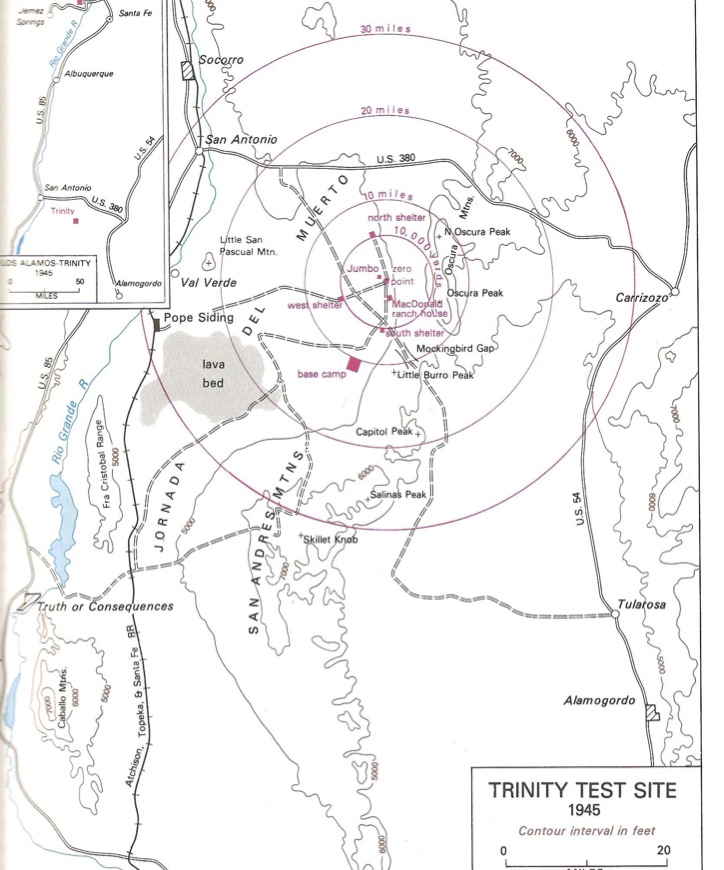
Карта полигона Тринити [wiki]. Можно заметить отметку базового лагеря (Квадратик - Место нахождения Э.Ферми во время взрыва) на десятимильной окружности.

Вид сверху через 28 часов после взрыва [wiki].

На следующем сайте обсуждаются вопрос как раскрыть метод, которым пользовался Ферми при определении мощности первого атомного взрыва:

[9] Quora: https://www.quora.com/How-did-Fermi-estimate-the-power-of-the-Trinity-bomb

Еще один подход предложен в [Weinstein2012p169-171]. Здесь мощность взрыва оценивается в 1-4 кт.

Weinstein2012p169-171

Оценка мощности исходя из работы взрыва против атмосферного давления приведена в [Исакович1972p108-109]. Результат оценки, по мнению автора, совпадает с реальными данными для бомб данного типа. Однако, надо отметить, что первоначальные данные Ферми несколько отличаются от американских источников. В частности, бумажки улетели на 2.5 метра, а не 1, и Ферми находился в 16 км от эпицентра, а не в 10. Пересчет в соответствии с новыми данными приводит к мощности в 100 кт, что не соответствует оценке Ферми.

[10] Исакович1973: Исакович М.А. Общая акустика. Учебное пособие.- М.: Издательство «Наука», Главная редакция физико-математической литературы, 1973. - 496с. (с.108-109)

Также можно предположить использование для сравнения экспериментального неядерного взрыва, проведенного несколько ранее.

100-Tonn Test. Пробный взрыв, проведенный 7 мая 1945г. для исследования эффектов взрыва и настройки измерительных приборов. Состоял в подрыве 110 тонн ТНТ на башне высотой 20 футов. Разбрасывал ли Ферми свои листочки во время этого взрыва? И на каком расстоянии от эпицентра он при этом находился?
Высоту башни можно проверить по среднему росту людей, стоящих на площадке, или по высоте ступенек лестницы на первом плане.
http://www.lanl.gov/newsroom/picture-of-the-week/pic-week-16.php

http://tutankanara.livejournal.com/404864.html
Встретился старый советский плакат по данной теме. Первый взрыв в Тринити имел слишком малую мощность и не попал в данную таблицу.

Определение мощности ядерного взрыва. Метод Джефри Тейлора.

Geoffrey Ingram Taylor (1886-1975) оценил мощность взрыва в 17 кт, не имея данных об американских измерениях и обладая только фотографиями взрыва, опубликованными в 1947г.
How Big was the Bomb?//Irish Times.2014
https://thatsmaths.com/2014/09/18/how-big-was-the-bomb/

https://ru.wikipedia.org/wiki/Тейлор,_Джефри_Инграм

Не путать с Бруком Тейлором (Brook Taylor) (1685—1731) (Ряд Тейлора в математике) и Фредериком Тейлором (Frederick Taylor)(1856-1915)(НОТ - научная организация труда).

[11] Deakin_Taylor2011: Deakin, Michael A.B. (2011) G.I. Taylor and the Trinity test// International Journal of Mathematical Education in Science and Technology, 42:8, 1069-1079, DOI: 10.1080/0020739X.2011.562324
http://dx.doi.org/10.1080/0020739X.2011.562324

[12] Taylor2011: G.I. Taylor, The formation of a blast wave by a very intense explosion: I. Theoretical discussion. Proc. Roy. Soc. A 201 (1950), pp. 159-74 [Reprinted in The Scientific Papers of Sir Geoffrey Ingram Taylor, Vol. 3, G.K. Batchelor, ed., Cambridge University Press, Cambridge, pp. 493–509].
http://www3.nd.edu/~powers/ame.90931/taylor.blast.wave.I.pdf

[13] Taylor2011: G.I. Taylor, The formation of a blast wave by a very intense explosion: II. The atomic explosion of 1945. Proceedings of the Royal Society A 201, 1950, pp. 175-86 [Reprinted in The scientific papers of Sir Geoffrey Ingram Taylor, G.K. Batchelor. ed., Vol. 3, Cambridge University Press, pp. 510–521].
http://www3.nd.edu/~powers/ame.90931/taylor.blast.wave.II.pdf

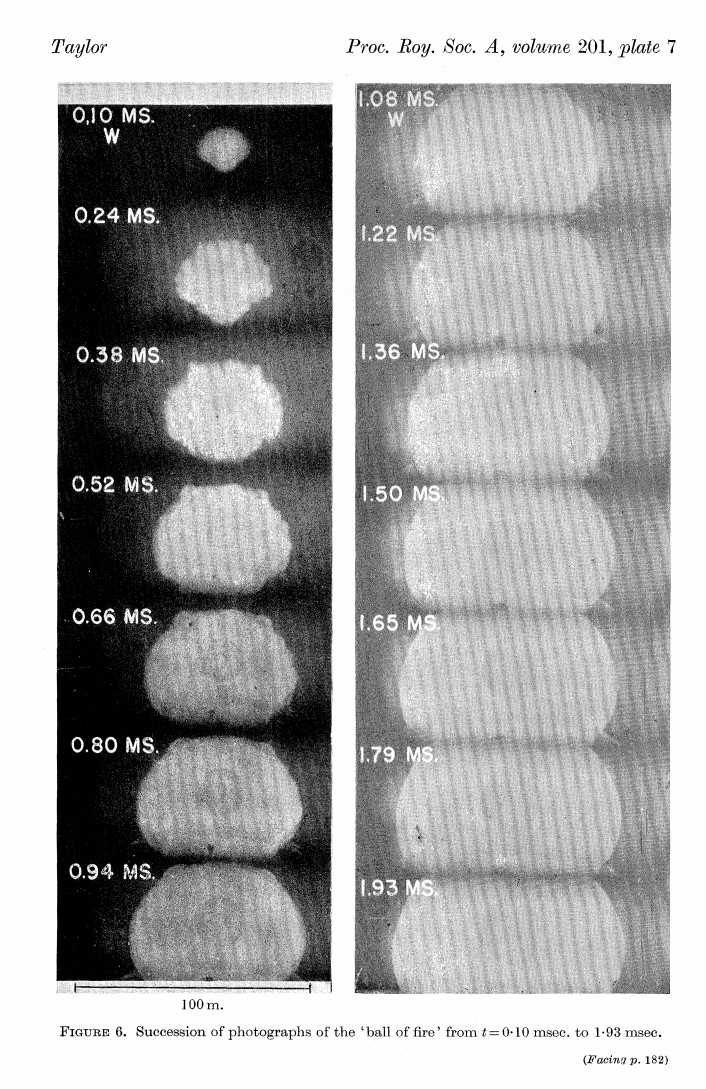
Рис. из статьи Тейлора

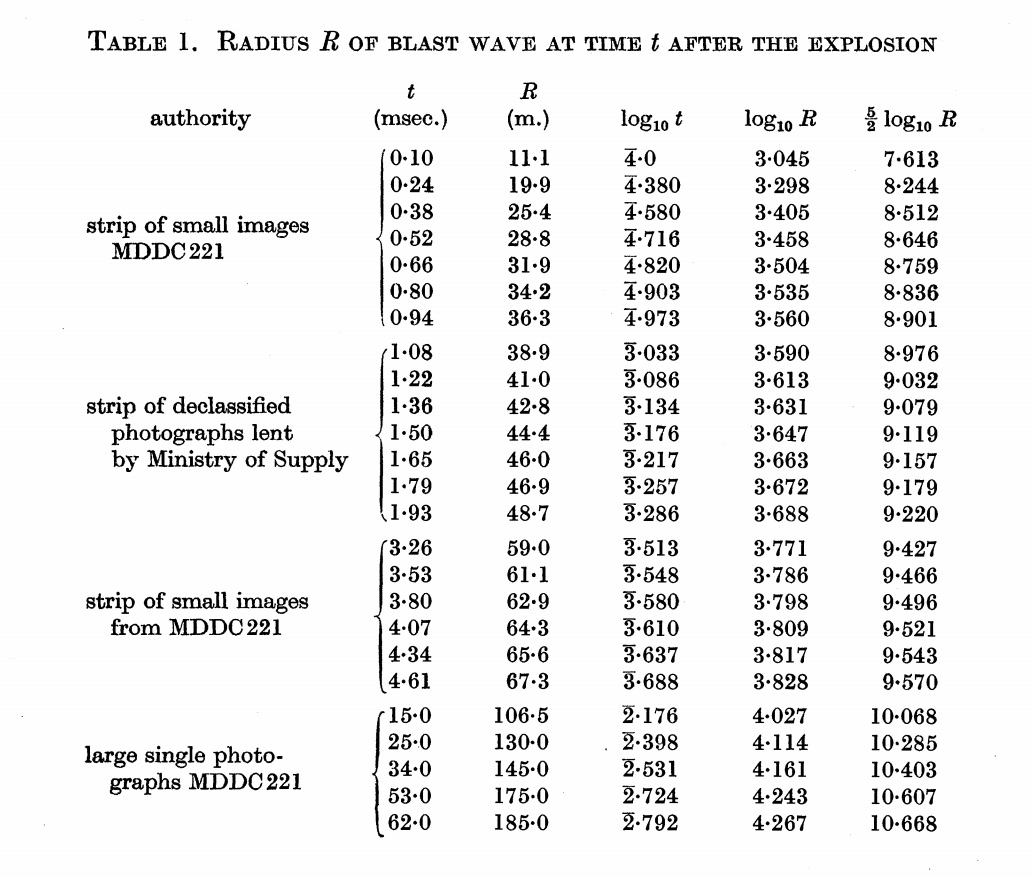
Таблица из статьи Тейлора

Итого: 16.8 тыс. тонн, не считая радиации.

[14] Mack1947: Mack, J. E. 1947 Semi-popular motion picture record of the Trinity explosion. PlIDDC221. U.S. Atomic Energy Commission. 44 pages
https://babel.hathitrust.org/cgi/pt?id=mdp.39015074121206;view=1up;seq=1

Эти фотографии использовал Тейлор, если судить по источникам в его статье.

[15] Бэрроу2014: Джон Бэрроу: История науки в знаменитых изображениях. - Пер. с англ. М: Эксмо, 2014. - 384с.
Ориг. назв.: John D. Barrow: Cosmic Imaginery: Key Images in the History of Science.

Эта чудовищная сила. Ядерный гриб. Расчет Тейлора. Снимки взрыва тоже присутствуют.[Бэрроу2014p318-320_377]

[16] Гровс1964: Гровс Л. Теперь об этом можно рассказать. - Сокращенный перевод с английского О.П. Бегичева - М.: Атомиздат, 1964. - 304c. (Глава 21. Аламогордо)
Leslie R. Groves: NOW IT CAN BE TOLD. The story of Manhattan project. - New York: Harper & Brothers Publishers, 1963.
https://ru.wikipedia.org/wiki/Гровс,_Лесли

Взрыв произошел сразу же после отсчета "ноль" в 5 часов 30 минут 16 июля 1945 г. Моим первым впечатлением было ощущение очень яркого света, залившего все вокруг, а когда я обернулся, то увидел знакомую теперь многим картину огненного шара. Первой моей, а также Буша и Конэнта реакцией, пока мы еще сидели на земле, следя за этим зрелищем, был молчаливый обмен рукопожатиями. Вскоре, буквально через 50 секунд после взрыва, до нас дошла ударная волна. Я был удивлен ее сравнительной слабостью. На самом деле ударная волна была не такой уж слабой. Просто вспышка света была так сильна и так неожиданна, что реакция на нее снизила на время нашу восприимчивость.

Ферми в тайне от всех приготовил очень простое приспособление для измерения силы взрыва -- клочки бумаги. Когда подошла ударная волна, я видел, как он выпустил их из руки. У земли ветра не было, поэтому ударная волна подхватила и отбросила их. Ферми отпускал их с определенной высоты, которую он заранее измерил, поэтому ему нужно было теперь только знать, на каком расстоянии они упали на землю. Он еще раньше вычислил зависимость силы взрыва от расстояния до него. Теперь, смерив расстояние до места, где упали клочки бумаги, он тотчас объявил, Какова была мощность взрыва. Его расчет совпал с данными, полученными позднее на основе показаний сложных приборов.

Накануне вечером я был несколько раздражен поведением Ферми, когда он вдруг предложил своим коллегам заключить пари -- подожжет ли бомба атмосферу или нет, и если подожжет, то будет ли при этом уничтожен только штат Нью-Мексико или весь мир. "Не так уже важно, -- говорил он, -- удастся взрыв или нет, все равно это интересный научный эксперимент, так как в случае неудачи будет установлено, что атомный взрыв невозможен".

§8.

[17] Morrison1963: Philip Morrison, Letters to the Editor, Am. J. Phys., August 1963, v31n8 p626-627
https://aapt.scitation.org/doi/10.1119/1.1969701

Philip Morrison (1915-2005):
https://en.wikipedia.org/wiki/Philip_Morrison
https://ru.wikipedia.org/wiki/Моррисон,_Филип
https://history.nasa.gov/EP-125/part3.htm>

Примеры задач Ферми:

#3 How much does a watch gain or lose when carried up a mountain?
Как поведут себя часы горах: будут спешить или идти медленнее и на сколько?
[Morrison1963]

Артур Комптон (1892-1962)(Нобелевская премия по физике 1927г. (НПФ-1927)) как-то сказал: «Энрико, когда я, исследуя космические лучи, бывал в Андах, то заметил, что на больших высотах мои часы идут неверно. Я долго искал объяснение и наконец нашел такое, которое меня удовлетворило. Чтобы вы могли сказать по этому поводу?» Ферми нашел листок бумаги, карандаш и вытащил свою карманную логарифмическую линейку. Буквально за несколько минут он вывел формулы для увлечения воздуха балансом часов, которое должно было увеличивать момент инерции баланса и тем самым замедлять ход часов. Рассчитав этот эффект, он получил цифру, почти совпадающую с ошибкой хода часов, которую Комптон наблюдал в Андах.
[Сегре1973p189]

{Конечно, здесь идет речь о механических часах.}

#4 How many piano turners are there in the city of Chicago?
Сколько настройщиков пианино в городе Чикаго?
[Morrison1963]

#5 What is the photon flux at the eye from a faint visible star?
Сколько фотонов попадает в глаз от слабо различимой звезды?
[Morrison1963]

#6 How far can a crow fly?
Как далеко может полететь ворона?
[Morrison1963]

#7 How many atoms could be reasonably claimed to belong to the jurisdiction of the United States?
Сколько атомов относится к юрисдикции Соединенных Штатов?
[Morrison1963]

#8 What is the output power of a firefly, a French horn, an earthquake?
Какова мощность жука-светлячка, музыкальной трубы, землетрясения?
[Morrison1963]

§9.

[18] Холидей1992: Холидей Д. Ошеломляющее впечатление (Задачи Ферми) //Квант. № 9. 1992. С.42-44. Два источника:
http://vivovoco.astronet.ru/VV/Q_PROJECT/HEAP/92_09_2/92_09_21.HTM
http://kvant.mccme.ru/1992/09/oshelomlyayushchee_vpechatleni.htm

Оригинал:

[19] Halliday1990: Halliday David(1916-2010)(University of Pittsburgh): Ballpark Estimates (Fermi Problems): How to impress your date and amaze your friends with off-the-cut answers to questions of magnitude// Quantum: The Magazine of Math and Science, May 1990, p.30-31.
На русском языке перевод названия оригинальной статьи звучит следующим образом:
Приблизительные оценки (Задачи Ферми): как произвести впечатление на свидании и поразить своих друзей оригинальными ответами на вопросы о величинах.
https://www.nsta.org/publications/quantum.aspx

#9 Сколько атомов резины стирается с шины автомобильного колеса при каждом его обороте?
[Холидей1992p42]

#10 В 1980 году население города Бостона составляло 560 000 человек. Сколько школьных учителей было в городе в том году?
[Холидей1992p44]

#11 Сколько галлонов бензина ежегодно сжигают все частные автомашины в США?
[Холидей1992p44]

#12 How far does a car travel before a one-molecula layer of rubber is worn off the tires?
Как далеко уедет автомобиль, пока сотрется слой резины толщиной в 1 молекулу?
[Weinstein_Adam2008p107(раздел 5.6)]

Практический вывод: можно считать, что при каждом обороте колеса стирается слой в одну молекулу [Weinstein_Adam2008p108].

§10.

[20] Adam1995: John A. Adam: Educated Guesses (Fermi Problems)// Quantum: The Magazine of Math and Science, Sept/Oct 1995, p.20-24.
Список номеров журнала Quantum:
https://www.nsta.org/publications/quantum.aspx
Сама статья на с.20-24(грузится очень медленно):
http://static.nsta.org/pdfs/QuantumV6N1.pdf
А здесь вырезка статьи, грузится побыстрее:
Adam.Guesses.1995

[Изображение с суперобложки Adam A. John: X and the City. - Princeton and Oxford: Princeton University Press, 2012. - 319p.]

Ссылается на три источника:
David Halliday: Ballpark Estimates//Quantum (may, 1990).
Сколько молекул резины стирается за один оборот колеса?
John Allen Paulos: Innumeracy.
John Harte: Consider a Spherical Cow.

#13 1. How many golf balls does it take to fill a suitcase?
Сколько мячей для гольфа наполнят чемодан?
[Adam1995p21]

#14 2. How many pieces of popcorn does it take to fill a room?
Сколько кусочков попкорна заполнят комнату?
[Adam1995p21]

#15 3. How many soccer balls would fit in an average-size home?
Сколько футбольных мячей поместится в средних размеров доме?
[Adam1995p21]

#16 4. How many cells are there in a human body?
Сколько клеток в человеческом теле?
[Adam1995p21]

#17 5. How many grains of sand would it take to fill the Earth?
Сколько нужно взять песчинок, чтобы заполнить ими всю Землю (именно всю, а не только поверхность)
[Adam1995p21]

#18 6. What is the volume of human blood in the world?
Какой объем занимает вся человеческая кровь?
[Adam1995p21]

#19 7. How many one-gallon buckets are needed to empty Loch Ness (and thus expose the monster)?
Сколько нужно одногаллоных ведер, чтобы вычерпать все озеро Лох-Несс в Шотландии и оставить чудовище без воды?
[Adam1995p21]

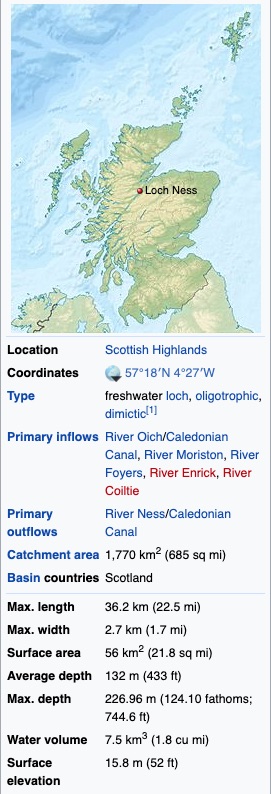https://en.wikipedia.org/wiki/Loch_Ness

{По данным из Wikipedia и интернета площадь озера Лох-Несс составляет 56 км². Максимальная глубина составляет 230м.
Средняя глубина - 132 м. Средняя глубина по определению - отношение объема воды к площади поверхности.
Объем воды в озере:
7.4 км³ = 7.4*10⁹ м³ = 7.4*10¹² литров
Поскольку в галлоне примерно 3.8 литра, то нам потребуется 2*10¹² одногаллоных ведер, чтобы вычерпать озеро Лох-Несс.
Если набирать 1 ведро в секунду, то потребуется где-то 63 тыс. лет. Данный способ вряд ли позволит в обозримое время очистить озеро от воды.
Однако можно по берегу озера разместить людей и поручить им черпать ведрами. Если площадь озера 56 кв. км и считать его квадратом, то по берегу будет примерно 30 км. Размещая по 1 человеку на метр, мы сможем вычерпать озеро уже за 2 года.}

#20 8. One gallon of paint is used to cover a building of area A. How thick is the coat?
Одним галлоном краски покрасили здание площади A. Какова толщина слоя краски?
{Не очень понятно: A - площадь здания или площадь покрашенной поверхности?}
[Adam1995p21]

#21 9. How much dental floss does a convict need?
Сколько нужно упаковок зубной нити, чтобы заключенные свили из нее веревку и спустились со стены высотой 18 футов?
[Adam1995p21]
Такой случай действительно произошел. Заключенные свили трос, толщиной с телефонный шнур и спустились со стены.

{ В статье приняты следующие исходные данные:
Толщина зубной нити (флосса) 0.5 мм при стандартной длине в 55 ярдов. Длину нити померить легко: вытащить из коробки и воспользоваться рулеткой или линейкой.
Толщину измерить сложнее. Хотя она может быть написана на коробке.
Толщина телефонного кабеля взята за 4 мм.
Тогда для толщины 1 мм необходимо взять четыре нити, а для 4 мм потребуется примерно 64 нити.
Переведем футы в метры и ярды в метры:
18 футов = 5.5 метров - это высота стены.
55 ярдов = 50 метров - это длина одной нити.

50/5.5 = 9, одну нить можно свернуть 9 раз.
64/9 = 7.1 - потребуется упаковок.
Я бы для надежности взял 8 упаковок. Авторский ответ: 7.}

#22 10. Estimate the number P of piano tuners in a certain city or region.
Оцените число настройщиков пианино в определенном городе или регионе.
[Adam1995p21]

#23 11. Estimate the number C (for cobbler) of shoe repairers in a city or region.
Оцените число сапожников, которые ремонтируют обувь в каком-либо городе.
[Adam1995p22]

#24 12. Estimate how fast human hair grows (on average) in mph.
Оцените скорость роста человеческих волос в среднем в милях в час (километрах в час).
[AAdam1995p22]

#25 13. Estimate the number of cigarettes smoked annually in the US.
Оцените число сигарет, выкуриваемых ежегодно в США.
[Adam1995p22]

#26 14. The asteroid problem. In the light of the impact of ex-commet Shoemaker-Levy on Jupiter's outer atmosphere, the question has been raised: could it happen here on Earth?
Задача (или уже проблема) астероида.
Комета Шумейкеров-Леви упала на Юпитер в 1994г. Перед падением она распалась на 21 часть, каждая размером не более 2 км в диаметре. Могло ли это произойти на Земле?
[Adam1995p22]

#27 15. Thickness of an oil layer.
Толщина слоя масла, растекшегося по поверхности воды. Еще Бенджамин Франклин заметил, что 0.1 см² масла растекается на поверхности до 40 м².
[Adam1995p23]

#28 16. The number of leaves on tree.
Число листьев на дереве.
[Adam1995p23]

#29 17. Weekly supermarket revenue.
Ежедневная выручка супермаркета.
[Adam1995p23]
Адам рассматривает как среднее количество работающих касс, количество посетителей в кассе, средний чек и количество рабочих дней в неделе.

#30 18. Daily death rate in a city or region.
Ежедневный уровень смертности в городе.
[Adam1995p23]

#31 19. The number of blades of grass on the Earth.
Число травинок на Земле.
[Adam1995p23]

#32 20. What is the average depth of tread lost per revolution of a car tire?
Сколько в среднем стирается резины при одном обороте колеса?
[Adam1995p23]

#33 21. Population Square.
Площадь населения. Если все население Земли согнать на одну площадь, то каковы будут ее размеры. При этом предлагается разместить людей хоть и стоя, но комфортно. (На кв. метре четырех человек)
[Adam1995p23]

#34 22. Human surface area and volume.
Какие поверхность и объем всех людей?
[Adam1995p23]

#35 23. The average rate of growth of a child from birth to 18 years.
Средняя скорость роста ребенка до 18 лет. Как обычно, предлагается выразить ее в км/ч.
[Adam1995p24]

#36 24. Mean distance between two civilizations.
Среднее расстояние между цивилизациями.
[Adam1995p24]

§11.

Edward F. (Joe) Redish
Авторский сайт:
http://umdperg.pbworks.com/w/page/10511199/Joe%20Redish

Joe Redish: Selected Publications
http://umdperg.pbworks.com/w/page/10511204/Joe%20Redish%3A
%20Selected%20Publications

[21] Redish2002: University of Maryland Fermi Problems Site. These problems written and collected by E. F. Redish:
www.physics.umd.edu/perg/fermi/fermi.htm

Коллекция задач Ферми:
Общие - 31 задача
Механика - 13 задач
Колебания и волны - 3 задачи
Термодинамика и кинетичекая теория - 4 задачи
Электричество и магнетизм - 9 задач
Современная физика - 2 задачи.
Следующая ссылка на некоторые публикации по задачам Ферми.

Publications about Fermi problems.
http://www.physics.umd.edu/perg/fermi/fermref.htm

Articles:

John E. Carlson, "Fermi problems on gasoline consumption", The Physics Teacher, Vol. 35, No. 5, May 1997, pp. 308-309.

David Chandler, "How to split hairs on Fermi questions", The Physics Teacher, Vol. 28, No. 3, March 1990, p. 170.

M. St. John and Fred Reif, "Teaching physicists' thinking skills in the laboratory", American Journal of Physics, Vol. 47, 1979, p. 950.

Victor F. Weisskopf, "Search for Simplicity: Mountains, waterwaves, and leaky ceilings", Am. J. Phys., Vol. 54, No. 2, February 1986, pp. 110 -111

Books
Hans Christian von Baeyer, The Fermi Solution (Random House, NY, 1993).

Jearl Walker, The Flying Circus of Physics with Answers (John Wiley and Sons, NW, 1977).

§12.

[22] Purcell1984: Purcell, Edward M.(1912-1997)(НПФ-1952): The Back of the Envelope: A column in the American Journal of Physics (Am. J. Phys.). Jan 1983 - July 1984.

Колонка "На обороте конверта" в "Американском журнале физики" (январь 1983-июль1984). Всего 57 задач. Задачи также приведены на сайте Массачусетского технологического института (MIT).

Обзор содержания:
http://www.vendian.org/envelope/dir0/column_purcell.html

На сайте MIT'а приведены 72 задачи:
http://web.mit.edu/rhprice/www/Readers/backEnv.html

#37 Classical Mechanics-5: Как спрыгнуть с астероида.
[Purcell1984]

#38 Classical Mechanics-12: Если сбросить баскетбольный мяч с высоты небоскреба, на какую высоту он отскочит?
[Purcell1984]

#39 Thermodynamics and Energy-6: Сколько баррелей нефти потребляет 60-ваттная лампочка за год?
[Purcell1984]
(Пересчет через энергию, 1 баррель)

#40 Thermodynamics and Energy-7: Определите энергию, которую Земля получает от солнца за 1 день.
[Purcell1984]

#41 Thermodynamics and Energy-10: Если всю годовую выработку электроэнергии в США использовать для поднятия каменных глыб, то каков размер горы, собранной из этих глыб?
[Purcell1984]

#42 Electromagnetism-5: За какое время по линии передач передается энергия, необходимая для выплавки алюминия, содержащегося в этой линии передач.
[Purcell1984]

#43 Miscellaneous-8: Placing the contents of the Library of Congress on a postcard (Можно ли разместить все книги Библиотеки Конгресса на одной почтовой карточке?)
[Purcell1984]

§13.

[23] Бентли2002: Джон Бентли Жемчужины программирования. - 2-е изд. - СПб: Питер, 2002. - 272с.
Ориг. назв.: Bentley, Jon: Programming Pearls (2nd Edition) - New York: ACM Press, 2000. - 239p. (Column 7: The Back of the Envelope, p.67-76)
Пред. издание: Бентли Дж. Жемчужины творчества программистов. -М: Радио и связь, 1990. - 224с. (Гл.6 Предварительные оценки. с. 77-88)

Глава 7. Предварительные оценки (Column 7: The Back of the Envelope) с. 89-98.
(Basic Skills. Performance Estimates. Safety Factors. Little's Law. Principles. Problems. Further Reading. Quick Calculations in Everyday Life.)

Бентли2002 (рис.):

Решения задач к главе 7. с.248-249.
Приложение 2. Умеете ли вы делать оценки? с.217-218.
1. Население США на 1 января 2000.
2. Год рождения Наполеона.
{Умер где-то в 1820г. в возрасте около 50 лет}
3. Длина реки Миссисипи-Миссури.
4. Максимальные взлетный вес Боинга-747.
5. Время распространения радиосигнала от Земли до Луны.
{Расстояние от Земли до Луны поделить на скорость распространения радиосигнала в просторечии именуемой скорость света}
6. Географическая широта Лондона.
7. Время одного оборота "Шаттла" вокруг Земли.
{90 минут}
8. Длина между башнями моста Golden Gate.
{Легко смотрится на Google Maps}
9. Количество подписей в Декларации Независимости.
10. Количество костей в теле взрослого человека.

#44 Первый вопрос: "Сколько воды вытекает из Миссисипи за день?". Ответ "столько же, сколько втекает" абсолютно точный, но совершенно бесполезный. Общий принцип ответа: оценить скорость течения, глубину и ширину, потом это все перемножить и привести к требуемому времени.
[Бентли2002p90]

#45 Если вам сложно запомнить количество секунд в году, а перемножить секунды в минуте, минуты в часах, часы в сутках, на количество дней в году вы по какой-то причине не можете или не хотите, то можно воспользоваться мнемоническим правилом: 3.155*10⁷ с в году, 3.155*10⁹ с в веке. Это π секунд равно нановеку (правило Тома Даффа (Tom Duff)).
[Бентли2002p92]

#46 Закон Литтла: Среднее количество объектов в системе равно произведению средней скорости ухода объектов из системы на среднее время, проводимое каждым из них в системе. Обычно еще берется, что входящий поток равен исходящему.
[Бентли2002p95]
https://ru.wikipedia.org/wiki/Закон_Литтла

#47 Правило 72.
[Бентли2002p91]

#48 Десять удвоений - это тысяча, 20 удвоений - миллион.
[Бентли.ЖемчужиныПрограммирования.2002,с.91]

Рекомендации к дальнейшему чтению ([Бентли2002p97]):
- Хафф Дарелл (Darrell Huff) Как лгать при помощи статистики [Хафф2016]
- Paulos, John Allen: Innumeracy: Mathematical Illiteracy and Its Consequences [Paulos2001]

§14.

[24] Charity1997: Mitchell N. Charity: A View from the Back of the Envelope
http://www.vendian.org/envelope/dir0/fermi_questions.html

Большой список сайтов с задачами Ферми. Последние изменения от февраля 2003г. Многие ссылки битые.

1. [25] Talamo1996: Fermi Problems by Sheila Talamo, декабрь 1996г.
http://web.archive.org/web/20020223173109/ http://mathforum.org/workshops/sum96/interdisc/sheila1.html

Две классических задачи Ферми с подробным разбором решения:

#49 How many piano tuners are in New York City?
Сколько настройщиков пианино в Нью-Йорке?
[Talamo1996]

#50 How many jelly beans fill a one-liter bottle?
Сколько конфет можно поместить в литровую бутылку?
[Talamo1996]

[26] Talamo1996: Sheila Talamo: Classic Fermi Questions with annotated solutions
http://web.archive.org/web/20021217012424/ http://mathforum.org:80/workshops/sum96/interdisc/classicfermi.html

Набор задач Ферми на общие темы:

#51 The mass of how many Ford Falcons is equal to the mass of the water in the swimming pool at the Brisbane Girls' Grammar School in Australia?
Масса скольки Форд Фалкон равна массе воды в бассейне школы в Австралии?
[Talamo1996]

#52 What is the mass in kilograms of the student body in your school?
Какова масса всех учащихся вашей школы?
[Talamo1996]

#53 How many golf balls will fill in a suitcase?
Сколько мячей для гольфа можно разместить в чемодане?
[Talamo1996]

#54 How many gallons of gasoline are used by cars each year in the United States?
Сколько галлонов бензина потребляется автомобилями каждый год в США?
[Talamo1996]

#55 How high would the stack reach if you piled on trillion dollar bills in a single stack?
Какую высоту будут иметь долларовые купюры, сложенные одна на другую, если общая сумма составит 1 триллион долларов?
[Talamo1996]

#56 Approximately what fraction of the area of the continental United States is covered by automobiles?
Какую часть площади США (континентальной) занимают автомобили?
[Talamo1996]

#57 How many hairs are on your head?
Сколько волос на вашей голове?
[Talamo1996]

#58 What is the weight of solid garbage thrown away by American families every year?
Какой вес твердого мусора, выбрасываемого американцами за год?
[Talamo1996]

#59 If your life earnings were doled out to you at a certain rate per hour for every hour of your life, how much is your time worth?
Определите стоимость вашего часа, разделив ваш доход за все время на количество часов.
[Talamo1996]

#60 How many cells are there in the human body?
Сколько клеток в теле человека?
[Talamo1996]

#61 How many individual frames of film are needed for a feature-length film?
Сколько отдельных кадров в полнометражном фильме?
[Talamo1996]

#62 How many pizzas will be ordered in your state this year?
Сколько пицц закажут в вашем штате в этом году?
[Talamo1996]

http://web.archive.org/web/20030113150744/ http://mathforum.org:80/workshops/sum96/interdisc/fermicollect.html

http://web.archive.org/web/20020902224251/ http://www.flaguide.org/cat/math/estimation/estimation7.htm

Fundamental Concepts of Century Physics: text by Eric Smith, 1993
размещенный Austin Gleeson,
Department of Physics, University of Texas at Austin

Отдельный раздел посвящен задачам Ферми:
http://www.ph.utexas.edu/~gleeson/httb/section1_3_3_5.html

1) Задача о числе настройщиков пианино в Чикаго подробно рассмотрена.
2) Далее рассматривается задача определения массы Земли.
3) Размер Земли определяется исходя из размера временных зон, причем считается, что одна зона соответствует 1 тыс. миль.
4) Нахваливается книга Innumeracy by J. A. Paulos.
5) Ставится задача нахождения массы Солнца.
6) Кто ходит быстрее: люди высокого роста или низкого? Как это соотносится с их ростом?

Margaret Taplin, Institute of Sathya Sai Education, Hong Kong
Teaching Values Through A Problem Solving Approach to Mathematics
https://www.mathgoodies.com/articles/teaching_values

Margaret Taplin, Institute of Sathya Sai Education, Hong Kong
Mathematics Through Problem Solving
https://www.mathgoodies.com/articles/problem_solving

[27] Goldstein_Sherwin1997: Prof. Gary R. Goldstein, Prof. Martin Sherwin: The Nuclear Age: Its Physics and History: Some Background: Estimation.
http://web.archive.org/web/20160503170500/ http://emerald.tufts.edu/as/physics/courses/physics5/estim_97.html

#63 1) How many hairs are on a head?
Сколько волос на голове?
[Goldstein_Sherwin1997]

Ответ: от 30 до 240 тысяч.

#64 2) How many grains of sand are there on all the beaches of the world?
Сколько песчинок на всех пляжах мира?
[Goldstein_Sherwin1997]

#65 3) How much oil is consumed in the US?
Сколько нефти потребляется в США?
[Goldstein_Sherwin1997]

Все три задачи с подробными решениями.

12. #66 How many ping-pong balls fit in a room?
Engineering Modeling; Estimations and Approximations. Ping-Pong Anyone?//San Jose State University, College of Engineering: http://web.archive.org/web/20060619011457/ http://www.engr.sjsu.edu/nikos/courses/engr10/pdf/pingpong.pdf

Reference: A.M.Starfield, K.A. Smith, A.L. Bleloch: “How to Model it; Problem Solving for the Computer Age”, McGraw-Hill, 1990.

[28] engr.sjsu.edu.2002: Introducing to Engineering: Fermi Problems//San Jose State University, College of Engineering:
http://web.archive.org/web/20120201084611/ http://www.engr.sjsu.edu/nikos/courses/engr10/fermi.htm

15 задач Ферми.

#67 2. Estimate the amount of each of the ingredients required to make the concrete used in all the interstate highways in California.
Оцените количество каждого из инградиентов, требуемых для производства бетона на всех хайвеях Калифорнии.
[engr.sjsu.edu.2002]

#68 10. In the 1989 Loma Prieta earthquake in California, approximately 2 million books fell off the shelves at the Stanford University library. If you were the library administrator and wanted to hire enough part-time student labor to put the books back on the shelves in order in 2 weeks, how many students would you have to hire?
В 1989г. землятресение Loma Prieta в Калифорнии сбросило около 2 млн. книг с полок в библиотеке Стенфордского Университета. Если бы вы были администратором библиотеки и перед вами стояла задача поставить эти книги на полки за две недели, то сколько бы студентов-почасовиков вы бы наняли?
[engr.sjsu.edu.2002]

#69 15. Estimate the cost of lighting your classroom during the entire year.
Оцените стоимость освещения вашей классной комнаты в течении целого года.
[engr.sjsu.edu.2002]

13. [29] BrainTeasers2000: Brain Teasers: The Boston Consulting Group.2000:
http://web.archive.org/web/20010302192935/ http://bcg.com/careers/interview_prep/brain_teasers.asp

Три задачи с решениями:

#70 How many pay phones are there on the island of Manhattan?
Сколько телефонных будок (платных телефонов) на Манхеттене?
[BrainTeasers2000]

#71 How many hotel-sized bottles of shampoo and conditioner are produced each year around the world?
Сколько бутылочек отельного размера с шампунем и кондиционером производится в мире за год?
[BrainTeasers2000]

#72 You are in a room with three light switches, each of which controls one of three light bulbs in the next room. Your task is to determine which switch controls which bulb. All lights are off. Your constraints are: you may flick only two switches and you may enter the room with the light bulbs only once. How would you set about determining which switch controls which bulb?
У вас три выключателя, которые включают три лампочки в соседней комнате. Ваша задача определить: какой выключатель подключен к какой лампочке. Все лампочки выключены. Но вы ограничены: щелкнуть можно только двумя выключателями, а в соседнюю комнату можно зайти только один раз.
[BrainTeasers2000]

14. `Back-of-the-Envelope' Calculations
(The Seven Habits of Highly Effective Astronomers)
{Рассматривается в §29}

§15.

Muehlhauser2013: Задачи Ферми:
https://www.lesswrong.com/posts/PsEppdvgRisz5xAHG/fermi-estimates
Статья написана Luke Muehlhauser (Люк Мюльхаузер) , Berkeley, California
Website: http://lukemuehlhauser.com

#73 Example 1: How many new passenger cars are sold each year in the USA?
Сколько новых легковых автомобилей продается в США каждый год?
[Muehlhauser2013]

Ссылки на книги и сайты:

1. Play Fermi Questions: сайт не работает.
2. Guesstimation (2008)
3. Guesstimation 2.0 (2011)
4. How Many Licks? (2009)
5. Ballparking (2012)
6. University of Maryland Fermi Problems Site:
http://www.physics.umd.edu/perg/fermi/fermi.htm
7. Stupid Calculations: http://www.stupidcalculations.com
8. Сообщество любителей оценивания: https://www.reddit.com/r/estimation

Книги Люка Мюльхаузера:
1. Luke Muehlhauser: Facing the Intelligence Explosion// 2013, Kindle Edition
https://www.amazon.com/Facing-Intelligence-Explosion-Luke-Muehlhauser-ebook/dp/B00C7YOR5QБ
2. Luke Muehlhauser: Design A Book With OpenOffice.Org Writer. - Scotts Valley, California, US: CreateSpace, 2008. - 136p.

§16.

Задачи Гауэрса:
Тимоти Гауэрс (Timothy Gowers)(1963-) Британский математик. Кембриджский университет.
https://ru.wikipedia.org/wiki/Гауэрс,_Уильям_Тимоти

[30] Gowers2012: How should mathematics be taught to non- mathematicians?
Как математикам учить нематематиков?

https://gowers.wordpress.com/2012/06/08/how-should-mathematics-be-taught-to-non-mathematicians/

Приведены 68 задач для обсуждения. Задачи Ферми занимают среди них видное место. Большое количество комментариев: предлагают новые задачи и новые источники.

#74 1. Сколько весит облако?
How much does a cloud weigh?
[Gowers2012]

#75 2. Сколько людей можно разместить на острове Уайт?
[Gowers2012]

#76 3. Сколько настройщиков пианино в Чикаго? (классическая задача Ферми)
[Gowers2012]

#77 4. Если средняя температура океанов поднимется на 1 градус, насколько поднимется уровень моря?
If the average temperature of the sea were to rise by a degree, then by how much would thermal expansion cause sea levels to rise?
[Gowers2012]

#78 5. Сколько молекул из последнего дыхания Сократа в вашей комнате?
How many molecules from Socrates’s last breath are in the room?
[Gowers2012]

[31] Раков2012: Раков Э.Г. Атмосфера в классе //Химия. №33 (678), 1-7.09.2004
http://him.1september.ru/article.php?ID=200403303
{Здесь речь о последнем вздохе Цезаря.}

#79 6. 7. Особенности безопасности авиаперелетов.
[Gowers2012]

#80 8. В сентября 2009 года в Болгарской лотерее подряд выпали шесть одинаковых цифр. Является это свидетельством, что лотереей манипулировали нехорошие люди?
[Gowers2012]
http://www.telegraph.co.uk/news/newstopics/howaboutthat/6202593/Bulgarian-lottery-picks-same-numbers-in-straight-draws.html

#81 9. История Салли Кларк, обвиненной (и ложно) в убийстве двоих своих детей на основании математики.
[Gowers2012]
https://en.wikipedia.org/wiki/Sally_Clark

[32] Schneps_Colmez2013: Leila Schneps and Coralie Colmez, Math on trial. How numbers get used and abused in the courtroom. NY: Basic Books, 2013. (First chapter: «Math error number 1: multiplying non-independent probabilities. The case of Sally Clark: motherhood under attack»)

[33] Batt2005: John Batt: Stolen Innocence. 2005

#82 10. Парадокс среднего. Отсылка к задаче 66.
[Gowers2012]

#83 11. 12. Как мы можем верить результатам опросов.
[Gowers2012]

#84 13. Как определить, что средняя глобальная температура изменяется?
[Gowers2012]

#85 14. Средняя глобальная температура в 1998г. выше, чем в 2011, значит ли это, что деятельность человечества не вызывает повышения температуры.
[Gowers2012]

#86 15. Сравнение цифр для мальчиков и девочек на экзаменах.
[Gowers2012]

#87 16. Мой дед пил, много курил и ругался матом и умер в 95 лет. Можем ли мы быть уверены, что курение вызывает рак легких.
[Gowers2012]

#88 17. Стиль игры в крикет.
[Gowers2012]

#89 18. Вопрос о замене газона перед домом на площадку для машин. Хорошо вам, плохо соседям. Трагедия общин.
[Gowers2012]

#90 19. Игры в стиле дилеммы заключенного.
[Gowers2012]

#91 20. Игры возмездия.
[Gowers2012]
https://gilkalai.wordpress.com/2009/01/13/the-retaliation-game

#92 21. Вдова умирает. Как поделить наследство между тремя детьми, не только с учетом стоимости, но и сентиментального значения.
[Gowers2012]

#93 22. В магазине покупатель долго набирает товары в большую тележку, а другой хочет купить одну вещь, но быстро. Как это все организовать?
[Gowers2012]

#94 23. Распределить что-то посредством голосования.
[Gowers2012]

#95 24. Насколько быстро работает фотоаппарат?
[Gowers2012]

#96 25. Почему мышь выживает при большом падении, а человек нет.
[Gowers2012]

#97 26. Как начинается Мексиканская волна? (Это волна в толпе людей, обычно на стадионах)
[Gowers2012]

#98 27. У вас чашка горячего кофе и холодного молока. Вы хотите выпить кофе через десять минут и как можно более горячим. Когда надо вылить молоко в кофе: сейчас, через 10 минут или в промежутке?
[Gowers2012]

#99 28. Вы перебегаете из одного терминала аэропорта в другой. Где-то быстро идете, а где-то едете на эскалаторе и идете. И незадача: у вас развязался шнурок. Когда лучше его завязать: остановившись в укромном местечке или стоя на эскалаторе?
[Gowers2012]

You are walking from one end of an airport terminal to the other. The airport has several moving walkways, and you need to stop to tie your shoelace. Assuming you want to get to the other end as quickly as possible, is it better to tie your shoelace while you are on a moving walkway or while you are between walkways?
[Gowers2012]
Первоисточник вопроса:
https://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle

#100 29. У вас много коробок, картонок и т.д. Вам надо упаковать вещи и погрузить их в автомобиль. Какой метод предпочтительнее?
[Gowers2012]

#101 30. Вы, вероятно, слышали, что до Солнца 150 млн. километров. Откуда мы можем знать это?
[Gowers2012]
https://en.wikipedia.org/wiki/Cosmic_distance_ladder https://terrytao.wordpress.com/2010/10/10/the-cosmic-distance-ladder-ver-4-1

#102 31. Вы должны выполнить несколько задач и знаете вероятность неудач каждой. В каком порядке их выполнять, чтобы минимизировать время выполнения всех задач.
[Gowers2012]
https://gowers.wordpress.com/2010/04/02/use-of-mathematics-ii/#comment-7032

#103 32. Сколько должно стоить одобрение лекарств компетентными органами. (в области здравоохранения)
[Gowers2012]

#104 33. Как установить цену, чтобы максимизировать прибыль.
[Gowers2012]
https://en.wikipedia.org/wiki/Giffen_good

#105 34. Шесть карт с различными числами на столе. Как их отгадать?
[Gowers2012]

#106 35. Вы в лабиринте? Разработайте метод, как из него выйти.
[Gowers2012]

#107 36. Как собирать паззл из кусочков.
[Gowers2012]

#108 37. Улучшают ли камеры дорожную безопасность. Сравнить двух учителей по успехам учеников. Влияние кока-колы на телепатию.
[Gowers2012]

#109 38. Доказательство защиты натуральной пищи от сердечных приступов.
[Gowers2012]

#110 39. На каком расстоянии можно увидеть Эмпайр Стате Билдинг?
[Gowers2012]

Tim Says:
June 8, 2012 at 7:47 pm | Reply
An excellent list of questions!
Here’s a suggestion for a trigonometry question.
Tim and Tom go to the 14th floor Sky Bar of their hotel in Helsinki. Tim looks to the sea with his binoculars and says: “Hey, I think I see a building over there! Maybe it’s that 25-storey hotel in Tallinn where I went last week?” Tom thinks a while and says: “No way, Tallinn is 80 km away! It has to be a ship or a mirage!” Who is correct, Tim or Tom?

#111 40. Вы покупаете стиральную машину за 250 фунтов, а вам предлагают пятилетнюю гарантию за 60. Нужна ли она?
[Gowers2012]

#112 41. Странник предлагает вам с другом 1000 фунтов, если вы договоритесь поделить их. Если не договоритесь, ничего не получите.
[Gowers2012]

#113 42. Как честно поделить одно место между тремя попутчиками с помощью кривой монетки?
[Gowers2012]

#114 43. Положительный ответ для редкой болезни.
[Gowers2012]

#115 44. Вы подъезжаете к перекрестку и видите красный свет. Ваши действия?
[Gowers2012]

#116 45. Волшебник с конвертами и парадокс Ньюкомба.
[Gowers2012]
https://en.wikipedia.org/wiki/Newcomb’s_paradox

#117 46. Диана Силвестер была изнасилована и убита в 1972 году. В 2006г. полиция обнаружила совпадение генных материалов с заключенным, сидевшим в тюрьме за 2 изнасилования.
[Gowers2012]
http://www.nytimes.com/2009/05/22/us/22dna.html

#118 47. Как определить размер налогов, чтобы максимизировать поступления.
[Gowers2012]

#119 48. Инвестиции виртуальных денег.
[Gowers2012]

#120 49. В 1985г. никто не думал о крахе Советского Союза. И только германский экономист Вернер Обст предсказал, что это произойдет в 1990. Было ли это действительным прогнозом или ему повезло и он ткнул пальцем в небо.
[Gowers2012]
Статья в Википедии о прогнозах развала Советского Союза:
https://en.wikipedia.org/wiki/Predictions_of_the_dissolution_of_the_Soviet_Union

#121 50. Как составлять случайные правильные предложения из заданного набора слов.
[Gowers2012]

#122 51. Задача на избыточность английского языка.
[Gowers2012]

#123 52. Вы страшно торопитесь, но перед вами очередь. Как определить, стоять в очереди или лезть напролом?
[Gowers2012]

#124 53. Вы производите галоши, но вдруг материалы подорожали на 10 фунтов/на штуку. Насколько вы повысите цену: на 10 фунтов, меньше, больше, совсем не повысите.
[Gowers2012]

#125 54. Как с помощью гнутой монеты определиться честно с другом?
[Gowers2012]

#126 55. Как убедиться, что монета нечестная?
[Gowers2012]

#127 56. Как распределить время с другом: друг хочет футбол и фильм, вы хотите фильм, но ненавидите футбол. А если ситуация повторяется каждую неделю?
[Gowers2012]

#128 57. Игорная задача: вы начинаете с одного фунта. Правила следующие: решка - ваша сумма утраивается, орел - вы теряете все заработанное и получаете запрет на дальнейшую игру. Что вы должны делать?
[Gowers2012]

#129 58. Автор вопроса хочет взвесить маленькую дочку. Она не хочет. Способ придуман давно: встать с ней на весы. А потом без нее. Однако точность шкалы на маленький вес лежит в районе 100г, а на большой - хорошо, если двести. Есть ли способ для более точного измерения?
[Gowers2012]

#130 59. Сколько нужно/можно потратить денег на отслеживание орбиты астероида, который может столкнуться с землей. Ученые говорят, что такая вероятность в течении пяти лет менее 1%. (Мне кажется, что ученые говорят о цифрах, меньших на сколько-то порядков)
[Gowers2012]

#131 60. Разработайте стратегию для крестиков и ноликов.
[Gowers2012]

#132 61. Политический блог получает много комментариев, среди них много тупых. Чтобы бороться с этим, разработана система, которая помещает комментарии пользователей с хорошей историей в вверх списка. Будет ли это хорошо работать?
[Gowers2012]

#133 62. В футбольной лиге участвует 20 команд. Они должны провести 38 матчей (по два каждая с каждой). В результате забастовки игроков, сыграли только 10 матчей. Однако по итогам года все равно надо перевести две команды в верхнюю лигу, а две - в нижнюю. Как это сделать честно по данным результатам.
[Gowers2012]

#134 63. Статья в Гардиан, где говорится, что быть пешеходом более опасно, чем велосипедистом.
[Gowers2012]
Zoe Williams:
https://www.theguardian.com/commentisfree/2012/aug/01/cyclists-like-pedestrians-must-get-angry

#135 64. Как определить численность барсуков на определенной территории.
[Gowers2012]
http://www.bbc.com/news/health-19637936

#136 65. Если вы бегун на длинные дистанции, то вы заботитесь о двух вещах: скорость и выносливость. Если побежите слишком быстро, то сил до конца не хватит. Стандартная стратегия: бежать постоянно, а в конце ускорение. Есть ли другая стратегия?
[Gowers2012]

#137 66. Задача о студентах в университете из разных школ.
[Gowers2012]
https://www.theguardian.com/education/2013/jan/13/state-school-graduates-job-potential

#138 67. Время от времени газеты сообщают, что самый старый человек в Британии умер. Можете ли вы оценить, как часто это случается.
[Gowers2012]

#139 68. Недавно в одном сообщении говорилось, что социальные работники не смогли предсказать смерть малыша от голода, который находился под присмотром матери. Как бы вы могли более точно интерпретировать это утверждение.
[Gowers2012]

#140 Доп. задача из комментариев:
Вы движитесь по тропинке, вдоль которой свисают спагетти на высоте рта. Какова должна быть их толщина, чтобы вы могли двигаться бесконечно, поедая столько энергии, сколько сжигаете при движении.
[Gowers2012]

§17.

Анекдот про Анастаса Ивановича Микояна (1895-1978), опытного руководителя и дипломата, продержавшегося на советском политическом олимпе "от Ильича (В.И.Ленина)(1870-1924) до Ильича (Л.И.Брежнева(1906-1982)":

"Как-то Микоян собрался уходить из гостей. Неожиданно на улице ударил проливной дождь, а у Микояна не оказалось зонта.
- Как же вы пойдете, товарищ Микоян? – обеспокоились хозяева дома.
- Ничего, - невозмутимо парировал Анастас Иванович. – Я между дождевых струй пройду…"

https://russia.tv/brand/show/brand_id/38627

[34] Walker2007: Jearl Walker (Cleveland State University): The Flying Circus of Physics. - 2-nd edition. - Hoboken, NJ: Wiley, 2007. - 334p.
Расширение книги на сайте:
http://www.flyingcircusofphysics.com

#141 Run or walk in the rain?
Что делать под дождем: идти или бежать?
[Walker2007p1.]

Идет дождь. Надо бежать или идти? [Паундстоун2013p180]

Существует старинная городская легенда, что, если ехать на кабриолете достаточно быстро, то дождь не намочит ездоков.
Проверкой занимались в телепередаче:

[35] MythBusters2009: MythBusters (2009 season), Episode 124 – "Car vs. Rain". Original air date: June 17, 2009.
https://en.wikipedia.org/wiki/MythBusters_(2009_season) #Driving_in_the_Rain_in_a_Convertible

Автомобиль ехал со скоростью 140 км/ч, салон остался сухим, но подобная скорость была признана опасной на мокрой дороге.

Резюме: Правдоподобно, но не рекомендуемо.(Plausible, but not recommended).

§18.

Паулос Джон Аллен (Paulos John Allen) (1945-) - профессор математики в Temple University, Philadelphia.
Статья в Википедии:
https://en.wikipedia.org/wiki/John_Allen_Paulos

Личный сайт: https://math.temple.edu/~paulos

Фото с личного сайта: https://math.temple.edu/~paulos/

[36] Паулос2007: Джон Паулос: Математик играет на фондовой бирже. - М: Изд-во ОМЕГА-Л, 2007. - 240с. Напечатано инвестиционно-брокерской компанией "Старфин". В РГБ и РНБ нет.
Ориг. назв.: John Allen Paulos: A Mathematician Plays the Stock Market. - New York: Basic Books, 2003. - 216p.

[37] Paulos2013: John Allen Paulos: A Matematician Read the Newspaper. - New York: BASIC BOOKS, 2013. - 212p. - Библ. с. 205-206.

[38] Paulos2015: John Allen Paulos: A Numerate Life. A mathematician explores the vagaries of life, his own and probably yours. - Amherst, New York: Prometheus Books, 2015. - 206p. - Notes p.189-197.

[39] Paulos2010: John Allen Paulos: How Much Oil’s Spilling? It’s Not Rocket Science, 23.05.2010//ABC News
https://abcnews.go.com/Technology/WhosCounting/oil-spilling-gulf-mexico-bp-basic-calculations/story?id=10705575

Сколько нефти вытекает из трубы в Мексиканский залив. И насколько компания BP занижает это количество.

[40] Paulos1980: John Allen Paulos: Mathematics and Humor. - Chicago: The University of Chicago Press, 1980. - 116p.

[41] Paulos2009: John Allen Paulos: Irreligion: A Mathematician Explains Why the Arguments for God Just Don't Add Up. - New York: Hill and Wang, 2009. - 158p.

[42] Paulos2000: John Allen Paulos: I Think, Therefore I Laugh. - New York: Columbia University Press, 2000. - 178p.

[43] Paulos2001: John Allen Paulos: Innumeracy: Mathematical Illiteracy and Its Consequences. - New York: Yill and Wang, 2001. - 180p.

Паулос отмечает хорошие продажи биографий известных математиков, популярность ряда кинофильмов, пьес и книг математической направленности [Paulos2001px]:

1. Биография Paul Erdos:

[44] Hoffman1998: Paul Hoffman: The Man Who Loved Only Numbers. The Story of Paul Erdos and the Search for Mathematical Truth. - New York: Hachette Books, 1998. - 302p.

[45] Kanigel2016: Robert Kanigel: The Man Who Knew Infinity. A Life of the Genius Ramanujan. - NY: Washington Square Press, 2016. - 438p.

[46] Назар2017: Сильвия Назар Игры разума. История жизни Джона Нэша, гениального математика и лауреата Нобелевской премии. - Пер. с англ. А.Аракеловой, М.Скуратовской, Н.Шаховой. - М: Издательство АСТ: CORPUS, 2017. - 752с.
Ориг. назв.: Sylvia Nasar: A Beautiful Mind. The Life of Mathematical Genius and Nobel Laureate John Nash. - New York: Simon and Schuster Paperback, 1998. - 462p. - Bibliography p.437-439.
По книге в 2001г. снят фильм "Игры разума" (A Beautiful Mind). Режисер Рон Ховард (Ronald William Howard). В главной роли Рассел Кроу (Russell Crowe).

https://ru.wikipedia.org/wiki/Умница_Уилл_Хантинг
Официальный сайт фильма:
https://www.miramax.com/movie/good-will-hunting

[47] : Michael Frayn: Copenhagen. - New York: Anchor Books, 2000. - 144p.

[48] Auburn2001: David Auburn: Proof. - New York:  FSG Adult; 1st edition, 2001. - 83 p.

[49] Сингх2000: Сингх, Саймон Великая теорема Ферма. История загадки, которая занимала лучшие умы мира на протяжении 358 лет. - М: МЦНМО, 2000. - 288с.
http://ega-math.narod.ru/Singh/FLT.htm
Ориг. назв. Fermat’s last theorem. The story of a riddle that confounded the world’s greatest minds for 358 years.

[50] Глейк2001: Глейк Джеймс: Хаос. Создание новой науки. - СПб: Амфора, 2001. - 398с. - Тираж 6000.
Ориг. назв.: James Gleick: Chaos: Making a New Science. 1987. Русская транскрипиция фамилии - согласно издания.

Вопросы Паулоса:

#142 1. What the population of USA is?
Каково население США.
[Paulos2001p8]

#143 2. Approximate distance from coast to coast
Оцените расстояние от одного берега США до другого.
[Paulos2001p8]

#144 3. Roughly what percentage of the world is Chinese?
Грубо: какой процент мирового населения составляют китайцы?
[Paulos2001p8]

#145 4. Estimate how fast human hair grows in miles per hour?
Оцените, какова скорость роста человеческих волос в милях в час?
[Paulos2001p8]
(10^-8 миль в час.)

#146 5. Approximately how many people die on earth each day?
Приблизительно, сколько людей на Земле умирает каждый день?
[Paulos2001p11]
(2.5*10⁵)

#147 6. How many cigarettes are smoked annually in this counry?
Сколько сигарет выкуривают в этой стране (США) ежегодно?
[Paulos2001p11]
(5*10¹¹)

#148 7.How many pizzas are consumed each year in the United States?
Сколько пицц поедается каждый год в США?
[PPaulos2001p14]

#149 8.How many words have you spoken in your life?
Сколько слов вы произносите в течении жизни?
[Paulos2001p14]

#150 9. How many different people's names appear in the New York Times each year?
Сколько различных имен людей появляется в New York Times за год?
[Paulos2001p14]

#151 10. How many watermelons would fit inside the U.S. Capitol building?
Сколько дынь поместится в здание Конгресса?
[Paulos2001p14]

#152 11. What is the volume of all the human blood in the world?
Каков объем всей крови человечества?
[Paulos2001p14]
{4 литра на человек, всего 6 млрд. человек и 2.4 * 10¹⁰ литров крови. Поскольку в куб. метре 1000 литров, то общее количество крови составит 2.4 * 10⁷ куб. метров.
Далее Паулос размещает эту кровь в кубе со стороной 870 футов, отмечает, что она зальет Центральный парк в Нью-Йорке с глубиной 20 футов (около 6 м) , а также повысит уровень Мертвого моря (озеро на границе Израиля и Иордании) на три четверти дюйма (около 2 см) }

#153 12. Насколько сверхзвуковой Конкорд быстрее улитки?
[Paulos2001p15]

В 400 тыс. раз.

#154 13. How long would it take dump trucks to cart away an isolated mountain, say Japan's Mount Fuji, to ground level?
[Paulos2001p15]
Сколько времени потребуется, чтобы вывезти гору Фуджи на грузовиках?

#155 14. Всемирный потоп продолжался 40 дней и 40 ночей. Земля была покрыта слоем воды от 10 до 20 тыс. футов. На 1 час приходится 15 футов (где-то около 5 метров). Достаточна ли мощность данного потока, чтобы утопить любой ковчег?
[Paulos2001p16]

#156 15. Задача Паскаля: Which event was more likely: obtaining at least one 6 in four rolls of a single die, or obtaining at least 12 in twenty-four rolls of a pair of dice?
Что более вероятно, одна шестерка (по крайней мере) из 4 бросков, или 12 очков из 24 одновременных бросков двух костей?
[Paulos2001p28]

Ответ: вероятность выпадения 6 из четырех бросков - 0.52, выпадения 12 из 24 бросков - 0.49.

#157 16. Задача фон Неймана: Как бросить жребий кривой монетой?
[Paulos2001p29]

Надо бросить монету дважды. Если выпадут два орла или две решки, то надо повторить. Если выпадет последовательность орел-решка, то победила первая сторона, если решка-орел, то вторая.

#158 17. Задача последнего дыхания Цезаря: Какова вероятность, что вы в данный момент вдыхаете молекулу из последнего вздоха Цезаря?
[Paulos2001p31-32]

{А молекулы столько живут?}

#159 18. Сколько людей необходимо собрать вместе, чтобы день их рождения совпал хотя бы один раз с вероятностью 50%. Если собрать 367 человек, то вероятность станет 100%.
[Paulos2001p35-36]

Оказывается 23 человека. Только при этом совпадет не конкретный день, а какой-либо заранее не опреденный день в году.

19. Паулос, когда учился в колледже, написал письмо английскому философу и математику Бертрану Расселу (Bertrand Russel)(1872-1970). Рассел не только ответил на письмо студента, но и включил ответ в свою автобиографию, наряду с письмами Неру (Nehru)(1889-1964), Хрущеву (Khrushchev)(1899-1971), Элиоту (T.S.Eliot)(1888-1965), Лоуренсу (D.H. Lawrence)(1985-1930), Людвигу Витгенштейну (Ludwig Wittgenstein)(1889-1951).
[Paulos2001p40]

#160 20. В ресторане в гардероб сдают шляпы. Гардеробщик перемешал все номерки случайным образом. Какова вероятность, что хотя бы один посетитель уйдет в своей шляпе?
[Paulos2001p40-41]

Как не странно, 63%.

21. Некий консультант рассылает 32 000 писем, причем в 16 000 он указывает, что индекс поднимется, а в остальных, что, наоборот, упадет. На следующей неделе он рассылает только 16 000 писем, и только тем получателям, которым прислал верный прогноз на прошлой неделе. Далее таким же образом все сводится к 500 получателям писем, которые получили верные ответы. Они получают письмо с просьбой оплатить $500 за следующий прогноз.
[Paulos2001p42]

{Это работает, если получатели писем не общаются друг с другом. Подобная история рассматривается у Мартина Гарднера [Гарднер2010p138], у Нассима Талеба [Талеб2002p67-68]}

[51] Lehmann-Haupt1989: Christopher Lehmann-Haupt: Books of The Times; Dangers of Being a Nation of Number Numbskulls//New York Times, 23.01.1989:
https://www.nytimes.com/1989/01/23/books/books-of-the-times-dangers-of-being-a-nation-of-number-numbskulls.html

[52] wiki/Innumeracy_(book):  Описание книги Innumeracy в Википедии:
https://en.wikipedia.org/wiki/Innumeracy_(book)

[53] Paulos.Youtube.2013: Stories vs. statistics: Professor John Allen Paulos at TEDxTempleU:
https://www.youtube.com/watch?v=XVMYTplQ158

[54] Paulos2010: John Allen Paulos: Stories vs. statistics. //NYTimes.com,OCTOBER 24, 2010.
https://opinionator.blogs.nytimes.com/2010/10/24/stories-vs-statistics

§19.

Weinstein Lawrence (1960-)

Фото с третьего листа обложки Guesstimation 2.0

[55] Weinstein_Adam2008: Lawrence Weinstein, John A. Adam: Guesstimation: solving the world’s problems on the back of a cocktail napkin. - New Jersey: Princeton University Press, 2008. - 302 p. Библиогр. p.195-197 (31 назв.)

#161 3.1. Если все люди мира соберутся вместе, какую площадь они займут?
[Weinstein_Adam2008p21]

#162 3.2. Сколько мячей для гольфа расположатся по экватору?
[Weinstein_Adam2008p25]

#163 3.3. Если все банки с засолкой в США за год выставить в ряд, то насколько он протянется?
[Weinstein_Adam2008p29]

#164 3.4. Какова площадь поверхности полотенца?
[Weinstein_Adam2008p31]

#165 3.5. Сколько времени потребуется, чтобы заполнить собор Святого Павла водой из крана?
[Weinstein_Adam2008p35]

#166 3.6. Сколько весит моль кошек? (моль - это число атомов, которые образуют химический элемент, весящий в граммах столько же, каков атомный вес элемента).
[Weinstein_Adam2008p39]

#167 3.7. Сколько весят билеты лотереи и сколько грузовиков потребуется для их перевозки?
[Weinstein_Adam2008p41]

#168 3.8. Сколько весит весь мусор, собираемый в США за год?
[Weinstein_Adam2008p43]

#169 3.9. Сколько потребуется места на полигоне, чтобы разместить мусор из предыдущей задачи?
[Weinstein_Adam2008p47]

#170 3.10. Сколько человек находится в воздухе над территорией США в данный момент?
[Weinstein_Adam2008p51]

#171 3.11. Во время землетрясения в Калифорнии 2 млн. книг упали с полок. Сколько потребуется студентов, чтобы за недели вернуть их на место?
[Weinstein_Adam2008p53]

[56] Mann2008: Tony Mann: Отзыв на Guesstimation: Solving the World's Problems on the Back of a Cocktail Napkin
While Tony Mann risks buying ice-cream that might melt, others puzzle over fridge insurance and health. June 5, 2008
https://www.timeshighereducation.com/books/
guesstimation-solving-the-worlds-problems-on-the-back-of-a-cocktail-napkin/ 402275.article?storyCode=402275§ioncode=26

{Пока Тони Манн рискует купить мороженное, которое может растаять, кто-то ломает голову над страховкой холодильника и здоровьем...}

[57] Weinstein2012: Lawrence Weinstein(1960-): Guesstimation 2.0: solving the today’s problems on the back of a napkin. - Princeton, New Jersey: Princeton University Press, 2012. - 360 p. Библиогр. p.357-353 (33 назв.)

Atomic bomb and confetti, p.169-171

[58] Angier2009: Natalie Angier: The Biggest of Puzzles Brought Down to Size Basics//New York Times, March 30, 2009.
http://www.nytimes.com/2009/03/31/science/31angi.html
{Самая большая головоломка разделяется на части и приводится к решаемому размеру.}

[59] Weinstein2002: Prof L.B. Weinstein: Physics on the Back of an Envelope. Physics 309.//Old Dominion University Fermi Problems Site:
https://www.lions.odu.edu/~lweinste/wag.html

§20.

[60] Mahajan Sanjoy (1969-) Сайт автора:
http://web.mit.edu/sanjoy/www/

[61] Mahajan.Numbersight Consulting LLC: http://numbersight.com

[62] Mahajan2010: Sanjoy Mahajan(1969-): Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving. - Cambridge, Massachusetts: MIT Press, 2010. - 136 p. - Библиогр. p.123-125 (49 назв.)

[63] Mahajan2014: Sanjoy Mahajan(1969-): The art of insight in science and engineering. Mastering complexity. - Cambridge, Massachusetts: MIT Press, 2014. - 390 p. - Библиогр. p.359-361 (50 назв.)

https://ocw.mit.edu/resources/ res-6-011-the-art-of-insight-in-science-and-engineering-mastering-complexity-fall-2014/ online-textbook/MITRES_6-011F14_art_insfin.pdf

[64] Mahajan: Sanjoy Mahajan Numbersight: A Street-Fighting Mathematician Teaches How to Make Better Decisions. - Amherst, New York: Prometheus Books.
Еще не вышла.

https://www.amazon.com/gp/product/1938000102/ref=dbs_a_def_rwt_bibl_vppi_i2

[65] Mahajan1998: Thesis by Sanjoy Mahajan. Order of Magnitude Physics. A Textbook with Applications to the Retinal Rod and to the Density of Prime Numbers.
(In partial fulfillment of the requirements for the degree of Doctor of Philosophy.)
- Pasadena, California: California Institute of Technology, 1998. - 218p. - Библиогр. p.207-212 (66 назв.)
http://www.inference.org.uk/sanjoy/thesis/thesis-letter.pdf

§21.

[66] Santos: Aaron Santos, авторский сайт:
www.aaronsantos.com

[67] Santos2009: Aaron Santos: How many licks? Or, How to estimate Damn near anything. - Philadelphia, London, 2009. - 176p.

[68] Santos2011: Aaron Santos: Ballparking. Practical math for impractical sports question. - Philadelphia, London: Running Press, 2012. - 220p.

§22.

Clifford Swartz (1925-2010) Stony Brook University emeritus professor
Некролог:
https://www.newsday.com/long-island/obituaries/clifford-swartz-stony-brook-university-emeritus-professor-dies-1.2249921

[69] Swartz1993: Clifford E. Swartz: Used Math for the First Two Years of College Science. - 2 edition - College Park, MD: American Assn of Physics Teachers, 1993. - 264p. (First edition, 1973).

[70] Swartz2003: Clifford Swartz (1925-2010): Back-of-the-Envelope Physics. - Baltimore, Maryland: The Johns Hopkins University Press, 2003.- 176p.

#172 Задача факира, как лечь на кровать из гвоздей.
[Swartz2003p1]

#173 Задача о громе и молнии.
[Swartz2003p47]

#174 Задача о максимальной высоте гор на Земле.
[Swartz2003p106]

§23.

[71] Harte1988: Harte John(1939-) Consider a Spherical Cow. A Couse in Environmental Problem Solving. - Sausalito, California: University Science Books, 1988. - 283p. Biblio p.271-274 (79)

[72] Harte2001: Harte John(1939-) Consider a Cylindrical Cow. More Adventures in Enviromental Problem Solving. - Sausalito, CA: University Science Books, 2001. - 211p. Biblio p.207-208 (36)

§24.

[73] mathforum.org: Resources Related to Fermi Questions:
Через Web.Arhive.org:
http://mathforum.org/workshops/sum96/interdisc/fermilinks.html

§25.

[74] Youtube_Underwood2014: Fermi Problems Tutorial:
www.youtube.com/watch?v=nM3-pvmOE18

#175 Сколько нужно мячей для гольфа, чтобы заполнить ими Boeing 747?
[Youtube_Underwood2014]

#176 Сколько электронов пройдет через MacBook Air за время, пока он не потребит энергию в 1 млн. джоулей?
[Youtube_Underwood2014]

§26.

[75] Youtube_FermiProblems2016: Fermi Problems: from toilet paper to housing the world:
www.youtube.com/watch?v=_PEQCX0la2Y

8:20 Задачи Ферми, фото Ферми.

11:45 #177 How much toilet paper do we get through in New Zealand?
Сколько туалетной бумаги потребляется в Новой Зеландии?
[Youtube_FermiProblems2016]

18:00 #178 Нow many people are using Facebook right now?
Сколько людей в Фейсбуке прямо сейчас?
[Youtube_FermiProblems2016]

§27.

[76] Youtube_Clements2016: #179 Fermi Problem, Number of Oil Changes on One Day in USA (Как оценить количество машин в США, которые поменяют масло в следующий вторник):
https://www.youtube.com/watch?v=8KlYiMewTwk

§28.

[77] Youtube_Robinson2016: Frank Robinson: Introduction A Fermi Estimate:
https://www.youtube.com/watch?v=mFwU56_59zc

§29.

[78] www.fermiquestions.com: Play Fermi Questions: 2100 Fermi problems and counting: www.fermiquestions.com
Tutorial: http://www.fermiquestions.com/tutorial

§30.

[79] JoshOrter: Блог Josh Orter: www.stupidcalculations.com

§31.

[80] Olsen: Paul Eric Olsen: DINOSAURS AND THE HISTORY OF LIFE. Курс лекций. Из шестой лекции ссылка на метод Ферми: #180 как определить диаметр Земли, исходя из расстояния между Нью-Йорком и Лос-Анжелесом и разницей во времени между ними.
rainbow.ldeo.columbia.edu/courses/v1001/fermi.html

§32.

[81] Хаббард2009: Хаббард Д. Как измерить все, что угодно. Оценка стоимости нематериального в бизнесе.- Пер. с англ. Е.Пестеревой - М.: ЗАО "Олимп-Бизнес", 2009. с.9-11.
Hubbard, Douglas D.: How to measure anything: finding the value of intangibles in business. - Hoboken, New Jersey: John Wiley and Sons, 2014. Первое издание в 2007, второе - 2010. Русский перевод с первого издания.

[82] Выписки из книги Дугласа Хаббарда:
http://www.elitarium.ru/metod-fermi-ocenka-izmerenie-neopredelennost-reshenie-primer-navyk

[83] Дуглас Хаббард «Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе» — краткое содержание от 4brain.ru:
https://4brain.ru/blog/дуглас-хаббард-как-измерить-всё

§33.

[84] Baeyer1993: Hans Christian von Baeyer: The Fermi Solutions. - New York: Random House, 1993. - 173p. [Baeyer1993p3-12]

Упоминаются следующие задачи Ферми: мощность атомной бомбы, количество настройщиков пианино, истирание автомобильных шин, применение лазерного оружия, оценка ускорителя частиц и структуры кристалла, а также книга Роберта Персига "Дзен и искусство ухода за мотоциклом".

#181 Если от Нью-Йорка до Лос-Анжелеса 3 тыс. миль и три часа разницы, которые составляют одну восьмую всего дня, то можно предположить, что окружность Земли составит 24 тыс. миль [Baeyer1993p5]. Это хорошая оценка с высокой точностью. А теперь попробуйте посчитать эту же окружность на примере Москвы и Владивостока? Результат будет не столь радостный.

А как быть с перелетом Франкфурт - Лос Анжелес: 10 тыс. км, 9 часов разницы во времени? Земля получается не очень больших размеров.

#182 Задача из серии: у вас есть кувшины 8, 5 и 3 литра, как отмерить 1 л, может показаться похожей на задачу Ферми. Но это не так. Задача Ферми не имеет логического однозначного решения, а является аппроксимацией [Baeyer1993p6].

Задачи Ферми требуют знания фактов, которые не входят в формулировку задачи [Baeyer1993p6].

#183 Хорошим примером использования задач Ферми в области вооружений может служить оценка, предложенная David Hafemeister из Калифорнийского Политехнического Университета в 1981г. Сколько времени потребуется мощному лазеру, чтобы разрушить боеголовку приближающейся ракеты? Можно взять расстояние до ракеты (скажем семьсот миль, температуру разрушения материалы, размеры зеркала для фокусировки лазерного луча (это больше напоминает гиперболоид инженера Гарина), мощность лазера (рассматриваются миллионы Ватт). И получить ответ: 10 минут, что не очень устраивает заинтересованные стороны. Последний вопрос: какую часть семисот миль пролетит ракета за эти 10 минут? [Baeyer1993p8-9]

§34.

Паундстоун У. (William Poundstone)(1955-)

Авторский сайт: http://william-poundstone.com
Образование: физика, MIT.

Книги Паунстоуна У. Фото с авторского сайта.

[85] Паундстоун2014: Паундстоун У. Найти Умного. Как проверить логическое мышление и творческие способности кандидата. - М.: АЛЬПИНА ПАБЛИШЕР, 2014. - 266с.
Ориг. назв.: How Would You Move Mount Fuji? : Microsoft's Cult of the Puzzle—How the World's Smartest Companies Select the Most Creative Thinkers. - New York, Boston, London: Little, Brown and Company, 2004. - 276p.

с. 32 Кувшины. Есть 3 и 5, надо 7.
с.126 Два бикфордова шнура
с. 169 Настройщики пианино
с. 172 Бензоколонки в США
с. 173 Количество воды в Мисисипи
с. 175 Сколько весит весь лед на хоккейном катке
с. 182 Открыть наугад телефонный справочник
с. 184 Как разрезать прямоугольный торт
с. 196 Как отыскать нужную книгу в большой библиотеке.
с. 200 Взвесить 8 биллиардных шаров.
с. 212 Два ведра 3 и 5л. Надо отмерить 4.
с. 224 Туристы переправляются через реку.
с. 231 Как передвинуть гору Фудзи.
с. 237 Пять пиратов делят добычу.

Другое издание и название:

Паундстоун У. Как сдвинуть гору Фудзи? Подходы ведущих мировых компаний к поиску талантов.- М.: Альпина Бизнес Букс при содействии Headhunter.ru, 2004.
Ориг. назв: How Would You Move Mount Fuji? : Microsoft's Cult of the Puzzle—How the World's Smartest Companies Select the Most Creative Thinkers

[86] Паундстоун2013: Паундстоун У. Действительно ли вы умны, чтобы работать в Google? Коварные вопросы, головоломки в стиле дэен, предельно сложные задачи и другие сбивающие с толку приемы, которые применяют на собеседованиях и которые очень полезно знать, если вы хотите получить работу и найти свое место в новой экономике. - Пер. с англ. В.Егорова. - М.: Карьера Пресс, 2013. - 400с. Библиогр. с.382-387. (89 назв.) (Глава 8. Доктор Ферми и инопланетяне. с. 155-165)
Poundstone W.: Are You Smart Enough to Work at Google?: Trick Questions, Zen-like Riddles, Insanely Difficult Puzzles, and Other Devious Interviewing Techniques You Need to Know to Get a Job Anywhere in the New Economy. - New York, Boston, London: Little, Brown and Company, 2014. - 292p. (First edition 2012).

Какое число идет дальше? 10, 9, 60, 90, 70, 66 [Паундстоун2013p10].
Блендер и вы в уменьшенном варианте. [Паундстоун2013p17].
Полет на самолете туда и обратно при наличии ветра [Паундстоун2013p27].
Последовательность: sss,scc,c,sc Что дальше [Паундстоун2013p27].
Переправа 3 чел. и 3 львов на 1 лодке, львы не должны быть в большинстве. [Паундстоун2013p58].
Песочные часы на 4 и 7 минут, отмерить 9. [Паундстоун2013p58].
Оптимальное число монет на сдачу. [Паундстоун2013p58].
Сыр в форме куба. Сколько нужно разрезов, чтобы получить 27 кубиков? [Паундстоун.Google.2013,с.59].
Три коробки и парадокс Монти-Хилла [Паундстоун2013p59]
Шарик в автомобиле [Паундстоун2013p59]
В книге N страниц от 1 до N. Если сложить количество цифр в каждом номере страницы, то будет 1095. Сколько страниц в книге? [Паундстоун2013p73]
Почему крышки канализационных люков круглые? [Паундстоун2013p91]
Можно заводить детей до первого мальчика. Каково соотношение мальчиков и девочек в этой стране? [Паундстоун2013p249]
(Также Гамов.ЗанимательнаяМатематика.2001,с.15, Дела семейные)
Автомобиль за 30 мин. - вероятность 95%. Какова вероятность за 10 мин.? [Паундстоун2013p98].
Как лучше забросить баскетбольный мяч: с одного раза или два раза из трех? [Паундстоун2013p98].
Если вы получили бы стопку монет достоинством в 1 пенс каждая и высотой с Эмпайр-стейт-билдинг, поместились бы все эти деньги в одно помещение? [Паундстоун2013p117]
Кролики бегут на 100 метров, потом один получает фору. Кто быстрее? [Паундстоун2013p117]
Как принять справедливое решение с гнутой монетой [Паундстоун.Google.2013,с.118].
Вопросы Ферми: Сколько тенисных шариков поместится в этом помещении? [Паундстоун2013p135].
Цена за мойку всех окон в Сиэтле. [Паундстоун2013p141]
Сколько сидений подъемника вы встретите во время движения? [Паундстоун2013p141]
Последовательность и след. строка:
1/11/21/1211/111221 [Паундстоун2013p141p289]
Как разместить посетителей в баре? [Паундстоун2013p153]
Сколько насечек на ребре четвертака (25 центов)? [Паундстоун2013p165]
Сколько флаконов шампуня производится в мире за год? [Паундстоун2013p165]
Сколько рулонов туалетной бумаги потребуется, чтобы покрыть ею весь штат? [Паундстоун2013p165].
{Сколько деревьев уйдет на производство этой бумаги? Или она делается из вторсырья?} Сколько будет 2^64? [Паундстоун2013p164].
Сколько мячей для гольфа войдет в школьный автобус? [Паундстоун2013p165]
Идет дождь. Надо бежать или идти? [Паундстоун2013p180]
Набирать по очереди 1 или 2 шарика из кувшина. Выигрышная стратегия? [Паундстоун2013p180]
Парк из 50 грузовиков. Каждый заправлен и может проехать 100 миль. На какое расстояние можно доставить груз в пустыне, если нет заправок? [Паундстоун2013p180]
Как получить случаное число от 0 до 7 с помощью игральной кости с 5 гранями? [Паундстоун.Google.2013,с.181]
Ставить кирпичи друг на друга. [Паундстоун2013p181p337]
Как найти ближайшую пару звезд на небе? [Паундстоун2013p181]
Глава 10. Как взвесить собственную голову. [Паундстоун2013p182]
Архимед взвешивает корону. [Паундстоун2013p191]
Забег в 25 лошадей. [Паундстоун2013p289].
Ферми: Все знания взаимосвязаны. [Паундстоун2013p161].
Глава 8. Доктор Ферми и инопланетяне. [Паундстоун2013p155-165].
Жираф [Паундстоун2013p363]
Кардинальное правило вопросов Ферми: обходите углы в арифметике, но не в логике. [Паундстоун2013p162].

[87] Паундстоун2015: Паундстоун У. Камень ломает ножницы. Как перехитрить кого угодно: практическое руководство. М.: Азбука-Бизнес, Азбука-Аттикус, 2015. - 352 с.
Ориг. назв.: William Poundstone: Rocks break scissors. A practical guide to outguessing and outwitting almost everybody. - New York, Boston, London, Little, Brown and Compamy. -  307c. Библ. c. 287-296.
Другое название: William Poundstone: How to Predict the Unpredictable: The Art of Outsmarting Almost Everyone. - London: Oneworld Publications, 2014. Очень близка по содержанию. Указано, что originally published in United States as Rock Break Scissors by Little, Brown and Company, 2014.

[88] Паундстоун2017: Паундстоун У. Голова как решето: зачем включать мозги в эпоху гаджетов и Google. - Пер. с англ. А.Ковальчука. - М: Азбука Бизнес, Азбука-Аттикус, 2017. - 352с. Библиогр. с.342-350.
Ориг. назв.: Head in the cloud. Why knowing things still matters when facts are so easy to look up.

[89] Poundstone2019: William Poundstone: Нow to Predict Everything: The Formula Transforming What We Know About Life and the Universe. - London: A Oneworld Book, 2019. - 307p.

[90] Poundstone2019: William Poundstone: The Doomsday Calculation: How the Equation that Predict the Future is Transforming Everything We Know about Life and Universe. - New York, Boston, London: Little, Browen Spark, 2019. - 307p.
{Содержание полностью соответствует предыдущей работе, другое только название.
Фото на третьей странице суперобложки.}

[91] Калугин2013: Калугин Р. Вопросы Ферми при приеме на работу//09.02.2013
https://romankalugin.com/voprosy-fermi-pri-prieme-na-rabotu

Poundstone William. Bibliography

[92] : Big Secrets: The Uncensored Truth About All Sorts of Stuff You Are Never Supposed to Know (1983)

[93] : The Recursive Universe: Cosmic Complexity and the Limits of Scientific Knowledge (1984)

[94] : Bigger Secrets: More Than 125 Things They Prayed You'd Never Find Out (1986)

[95] : Labyrinths of Reason: Paradox, Puzzles, and the Frailty of Knowledge (1988)

[96] : The Ultimate: The Great Armchair Debates Settled Once and for All (1990)

[97] : Prisoner's Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb (1992)

[98] : Biggest Secrets: More Uncensored Truth About All Sorts of Stuff You Are Never Supposed to Know (1993)

[99] : Carl Sagan: A Life in the Cosmos (1999)

[100] : The Big Book of Big Secrets (2001) reprints Big Secrets and Biggest Secrets

[101] : How Would You Move Mount Fuji? : Microsoft's Cult of the Puzzle—How the World's Smartest Companies Select the Most Creative Thinkers (2003)

[102] : Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street (2005)

[103] : Gaming the Vote: Why Elections Aren't Fair (and What We Can Do About It) (2008)

[104] : Priceless: The Myth of Fair Value (and How to Take Advantage of It) (2010)

§35.

[105] Youtube_ADME.ru: 7 Самых Трудных Вопросов Соискателям за всю Историю Собеседований:
https://www.youtube.com/watch?v=dBpYgowQbCw

Хорошо сделанный 13-тиминутный ролик, ADME.ru

#184 1. Amazon: 80-метровый кабель свисает с двух шестов, оба высотой в 50м. Найдите расстояние между этими шестами до десятых долей, если середина кабеля висит на высоте 10м.
[Youtube_ADME.ru]

Определение длины провода в пролёте - Проектирование механической части ВЛ:
http://leg.co.ua/knigi/oborudovanie/proektirovanie-mehanicheskoy-chasti-vl-5.html

#185 2. Linkedin: 3 выключателя управляют 3 лампочками в соседней комнате. Как определить, какой выключатель управляет какой лампочкой?
[Youtube_ADME.ru]

#186 3. Adobe: У вас есть 50 мотоциклов и объема бензобака каждого из них хватит на 100 км. На какое максимальное расстояние вы сможете уехать с этими 50 мотоциклами?
[Youtube_ADME.ru]

#187 4. Microsoft: У вас есть тысяча бутылок сока. В одной из этих бутылок очень горький яд. Как узнать в какой он бутылке за наименьшее число глотков?
[Youtube_ADME.ru]

#188 5. Google: Почему крышки люков круглые?
[Youtube_ADME.ru]

#189 6. Facebook: Две пули друг за другом в пустом шестизарядном револьвере. Бараран раскручивается. И нажимает на на курок. Пустой, выстрела нет. Снова раскрутить барабан или сразу стрелять? Какова вероятность, что револьвер выстрелит в каждом из вариантов?
[Youtube_ADME.ru]

#190 7. Apple: Перед вами три коробки. В одной только яблоки, в другой - апельсины, в третьей яблоки и апельсины вместе. Все коробки помечены неверно. Сможете ли вы открыть 1 коробку, вытащить один фрукт, не заглядывая внуть, и правильно определить содержимое всех трех коробок по нему одному.
[Youtube_ADME.ru]

§36.

[106] Francis1999: Paul Francis, ANU Dept. of Physics. 25th February 1999: Back-of-the-Envelope Calculations Or: The Seven Habits of Highly Effective Astronomers
Семь навыков высокоэффективных астрономов.
http://www.mso.anu.edu.au/pfrancis/Approximations.pdf

Личная страница автора на сайте Австралийского Национального Университета, Канберра (ANU)(The Australian National University, Canberra):
http://www.mso.anu.edu.au/pfrancis

Задачи:

#191 Exercise 1: Roughly how many piano tuners are there in New York?
Оцените приблизительно количество настройщиков пианино в Нью-Йорке.
[Francis1999]

#192 Exercise 2: The car-park outside a shopping mall is completely full. You are cruising around in your car waiting for a space to become free. Roughly how long will you typically have to wait?
[Francis1999]
Парковка у торгового центра забита машинами. Вы ездите на автомобиле вокруг да около, пытаясь найти свободное место. Оцените, сколько времени это может потребовать?

#193 Exercise 3: If you connect a car engine up to a generator, how many light bulbs could it keep illuminated?
Если вы к двигателю вашей машины прикрутите генератор, то сколько лампочек к нему можно подключить?
[Francis1999]

#194 Exercise 5: If the maximum possible height of a mountain is set by the pressure at which the rocks at its base become plastic, and Mt Everest is roughly at the maximum height mountains can have on Earth, estimate the maximum possible height of mountains on Mars.
Предположим, что размеры гор ограничены по высоте тем, что гора своей тяжестью просто раздавит основание. Оцените, зная что на Земле самая высокая гора Эверест, какой должна быть самая высокая гора на Марсе?
[Francis1999]

#195 Exercise 6: Prove that all four-legged animals can jump to the same height.
Докажите, что все четвероногие животные могут прыгать на одинаковую высоту.
[Francis1999]

#196 Exercise 7: Deep in space, out near Pluto, lies the spaceship Canberra, Australia's first interstellar probe. Its weight, including the 27 astronauts, 46 sheep, 15 kangaroos, and 45 tonnes of meat pies, is 1327 tonnes. It has a nuclear reactor on board, which can generate a total energy output of 1018 J, in the process using up its entire fuel (50 kg of anti-matter, in the form of anti-tim-tams). This energy will be used to accelerate 40 tonnes of xenon gas, which will be fired out backwards to provide the rocket thrust. How long will it take the Canberra to arrive at Alpha Centauri, and will they have run out of meat pies by then?
Где-то в космических далях в районе Плутона пролетает первый австралийский межзвездный космический корабль Канберра. Его масса - 1327 тонн, включая 27 астронавтов, 46 овец, 15 кенгуру и 45 тонн мясных пирогов. На борту имеется ядерный реактор, который генерирует энергию в 1018 Джоулей, используя 50 кг антиматерии. Эта энергия используется для разгона 40 тонн инертного газа ксенона, который обеспечивает движение ракеты. Через сколько времени Канберра достигнет Альфа Центавра и хватит ли 45 тонн мясных пирогов для питания экипажа?
[Francis1999]

#197 An asteroid, one kilometre in diameter, lands in the North Atlantic. How high will the tidal waves be?
Астероид диаметром в 1 км приводнился в Северной Атлантике. Какой будет размер у вызванной этим событием волны?
[Francis1999]

§37.

[107] Рёслер2017: Вольфганг Рёслер: Физика, рассказанная на ночь. - СПб: Питер, 2017. - 384с. - Тираж 3000. Библиогр. с.377-383. (94 назв. На нем. яз.)
Ориг. назв.: Wolfgang Röbler: Eine Kleine Nachtphysik. Geschichten aus der Physik. - Basel,Boston,Berlin: Birkhäuser, 2007.

Леверье и новая планета [Реслер2017p95]

Вопросы Ферми [Реслер2017p119-126]

§38.

Хафф Дарелл (Darrell Huff) (1913-2001) - американский писатель.

[108] Хафф2016: Хафф Д. Как лгать при помощи статистики.- 2-е изд.- Пер. с англ. - М.: Альпина Паблишер, 2016. - 163с.
Ориг. назв.: Darrel Huff: How to lie with statistics. New York, London: W.W.Norton & Company, 1954.

Подробное описание книги:
https://ru.wikipedia.org/wiki/Как_лгать_при_помощи_статистики

[109] Huff1996: Darrel Huff: The Complete: How to Figure It: Using Math in Everyday Life. - New York: Norton, 1996.

§39.

[110] Wojzeh2016: Странные вопросы на собеседованиях 2016 (Отобраны вопросы, касающиеся темы данной работы) https://wojzeh.livejournal.com/1196945.html

Указан оригинал, там можно найти базу вопросов, задаваемых на интервью (если поискать):
https://www.glassdoor.com/List/Oddball-Interview-Questions-Canada-LST_KQ0,34.htm

#198 1. How do you calculate the number of red cars in a city?
Как бы вы посчитали количество красных машин в городе?
[Wojzeh2016]

#199 2. When a hot dog expands, in which direction does it split and why?
Когда хот-дог расширяется, в каком направлении он разломится и почему?
[Wojzeh2016]

#200 3. Would you rather fight 1 horse-sized duck, or 100 duck-sized horses?
Вы бы бились с одной уткой размером с лошадь или со ста лошадями размером с утку?
[Wojzeh2016]

#201 4. How many basketballs would fit in this room?
Сколько баскетбольных мячей поместится в эту комнату?
[Wojzeh2016]

#202 5. If you had $2,000, how would you double it in 24 hours?
Если бы у вас было 2000 долларов, то как бы вы их удвоили за 24 часа?
[Wojzeh2016]

#203 6. Если три человека в одной комнате, то какова вероятность, что хотя бы двое из них родились в один день недели?
[Wojzeh2016]

#204 7. Протянем по экватору Земли проволоку, плотно прижатую к поверхности. Теперь добавим к её длине один метр, и таким образом получим чуть большую окружность. Сможет ли мышь проскочить под проволокой?
[Wojzeh2016]

{Сможет.}

#205 8. Сколько АЗС в области Парижа?
[Wojzeh2016]

#206 9. Сколько шариков для пинг-понга поместится в школьный автобус?
[Wojzeh2016]

#207 10. Оцените количество людей в Париже, добирающихся на работу на велосипеде.
[Wojzeh2016]

#208 11. Сколько окон в Нью-Йорке?
[Wojzeh2016]

#209 12. How many hours would it take to clean every single window in London?
Сколько часов понадобится, чтобы вымыть каждое окно в Лондоне?
[Wojzeh2016]

{Несколько хороших идей в комментариях у

[111] mi3ch: https://mi3ch.livejournal.com/3304078.html

- Часами окна не моют...(имеет смысл только на русском языке)
- В Лондоне 10 млн. чел., по полтора окна на человека, итого 15 млн. окон. Мыть - по полчаса на окно - 7 млн. часов. }

#210 13. How do you get an elephant in a fridge?
Как бы вы поместили слона в холодильник?
[Wojzeh2016]

#211 14. If the time is quarter past 3, what is the angle measurement on the clock?
Если сейчас четверть четвёртого, какой угол образуют стрелки на часах?
[Wojzeh2016]

#212 15. How many people born in 2013 were named Gary?
Сколько рождённых в 2013 году людей получили имя Гари?
[Wojzeh2016]

#213 16. How many nappies are purchased per year in the UK?
Сколько подгузников покупается в год в Великобритании?
[Wojzeh2016]

§40.

[112] МатСост2015: Математическая составляющая / Редакторы-составители: Н.Р.Андреев, С.П.Коновалов, Н.М.Панюнин (Сотрудники лаборатории популяризации и пропаганды математики Математического института им. В.А.Стеклова РАН), Художник-оформитель Р.А.Кошкаров - М: Фонд "Математические этюды", 2015. - 151с. - Тираж 14 тыс. (осн.+доп.). - На сайте фонда "Математические этюды" (уже второе издание)

[113] МатСост2019: Математическая составляющая / Редакторы-составители Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин ; Художник-оформитель Р. А. Кокшаров. — 2-е изд., расш. и доп. (сильно расширенное) — М. : Фонд «Математические этюды», 2019. — 367 с. : ил. — ISBN 978-5-906825-02-5. — Тираж 17 000 экз. - На сайте фонда "Математические этюды":
http://book.etudes.ru

[МатСост2019p92]: Объем шкурки апельсина. В шаре почти половина объема сосредоточена у поверхности на расстоянии 1/5 радиуса:
book.etudes.ru/toc/orange

Кожуры и мякоти по объему - пополам.

[МатСост2019p93]: Конический фужер: половина по высоте - 7/8 объема. 1/5 по высоте сверху - половина объема.
https://book.etudes.ru/toc/glass

[МатСост2019p70]: Формат А4:
book.etudes.ru/toc/a4

[МатСост2019p82]: Измерение штангенциркулем:
book.etudes.ru/toc/vernier

[МатСост2019p82]: Сурдин В.Г. Високосное летосчисление:
book.etudes.ru/toc/chronology

[МатСост2019p60]: Расстояние до горизонта:
book.etudes.ru/toc/skyline

[114] Андреев2019: Андреев Н. Экскурсия по лаборатории популяризации математики.// Математический институт имени Стеклова. 31 мая 2019 г. Youtube: Савватеев А.: Мальткульт-привет.
https://www.youtube.com/watch?v=IzIewgnJXrA

[115] Андреев2016: Николай Андреев: Математическая составляющая //010. Академия Яндекса. 21 нояб. 2016 г.
https://www.youtube.com/watch?v=E15KN8_hpcE

§41.

Крылов Алексей Николаевич (1863-1945) - кораблестроитель, механик, математик, академик Петербургской АН и Академии наук СССР, заведующий опытовым бассейном, главный инспектор кораблестроения, генерал флота (Российская Империя), генерал для особых поручений при морском министре (Российская империя).

[Крылов1956, вставка после с.2]          [Wikipedia, 1910-е годы]

[116] Крылов1979: Крылов А.Н. Мои воспоминания. Л.: Кораблестроение, 1979. - 480c.
militera.lib.ru/memo/russian/krylov_an/index.html
Отрывки из воспоминаний:
vivovoco.astronet.ru/VV/PAPERS/BIO/KRYLOV/KRYLOV_29.HTM

Как были получены 500 миллионов на флот в 1912 году [Крылов1979,с.179-184].
vivovoco.astronet.ru/VV/PAPERS/BIO/KRYLOV/KRYLOV_15.HTM

Система М.И.Кази:

Есть еще и другая система, которой придерживался М.И. Кази, когда был директором Балтийского завода. Всякому писцу, доставившему копию официальной бумаги, в которой встречались слова «Балтийский завод», уплачивалось, независимо от содержания бумаги, пять рублей. Об этом при мне Михаил Ильич рассказал моему отцу, выразившему удивление, каким образом Михаил Ильич получил копию важнейшей бумаги и сколько это стоило.

— Пять рублей, — сказал Кази и рассказал свою систему. — За год приносят около тысячи копий, из них 995 и медного гроша не стоят, а вот за эту я бы и 10 000 руб не пожалел.

Подумайте о системе М.И. Кази.

[Крылов1979p222-223]

Статистика не должна состоять в одном только заполнении ведомостей размерами с двуспальную простыню никому не нужными числами, а в сведении этих чисел на четвертушку бумаги и в их сопоставлении между собою, чтобы по ним не только видеть, что было, но и предвидеть, что будет. [Крылов1979p196]

Как простейший анализ чисел позволяет выявить опечатки. {Академик} Бэр на Каспии

Мне {Крылову А.Н.} случайно попалась книга: М. Соловьев, «Бэр на Каспии». ..

{Соловьев М.М. (1877-1942) Бэр на Каспии. - М-Л: Изд-во Академии наук СССР, 1941. - 192с.
Доступна онлайн в Президентской библиотеке
https://www.prlib.ru/item/322307}

Внешность книги по шрифту, бумаге, рисункам не оставляет желать лучше­го, но значительное число опечаток или ошибок является недопустимым для академического издания. Приведу примеры:

1. Стр. 13. Сказано «Н. М. Книпович, тщательно его (Каспий — А. К.) изу­чивший с гидрологической и гидробиологической точек зрения, определяет объем Каспия в 79 319 куб. м. Каспий имеет площадь примерно в 436 340 кв. м».
В обоих случаях надо писать не метров (м), а км, т. е. километров, так что объем Каспия 79 319 куб. км, т. е. 79 319 000 000 000 куб. м, т. е. в милли­ард раз больше указанного.
Площадь Каспия 436 340 кв. км, т. е. 436 340 000 000 кв. м, т. е. в милли­он раз больше показанного.
{В настоящий момент (2018) площадь Каспийского моря составляет 371 тыс. кв.км}
Эта ошибка сразу бросается в глаза, ибо очевидно, что площадь не может быть равна 43,6 га.

2. Стр. 15. «Средний годичный улов на Каспии Бэр определял в 1856 г. в 12 млн пудов рыбы, на сумму около 10 500 000 руб. В одном только ниж­нем течении Волги выловлено в 1914 г., по Книповичу, 9041/2 млн голов раз­ной рыбы, весом около 231 400 т и стоимостью в 251/2 млн рублей золотом, а если сюда прибавить икру и другие продукты рыболовства, то улов опреде­лится в 294 480 т, стоимостью в 27 154 000 р. золотом».
Отсюда следует, что средняя цена за пуд улова в 1856 г. была 90 коп., а в 1914 г. — 1 р. 80 к. И «за разные продукты» — 45 коп. за пуд. Эти цифры следовало бы пояснить, распределив по рубрикам:
{Таблица в оригинале на с.348}
а то огульно они очень мало что выражают и вводят лишь читателя в за­блуждение.
Следовало бы также добавить цену мяса и цену хлеба.
Заметим также, что на стр. 174 сказано: «В 1855 г. , в связи с инструкци­ями, данными Бэром, ее (сельдь — А. К.) посолили уже полмиллиона штук, в 1877 г. — 210 млн, а в 1917 г. — 589,6 млн».
Но, кроме сельди, есть еще вобла, которой готовят тоже сотни миллионов штук, и без указанного подразделения по рубрикам число 904,5 млн не дает представления о рыболовстве на Каспии.

3. Стр. 16. «Особенно большими размерами среди них (каспийских рыб. — А. К.) отличается белуга... Это — крупнейшая из всех встречающихся в прес­ной воде рыб, достигает до 17 м длины».
Здесь «м» (метров) ошибочно. Следовало бы писать «футов».
Из рисунка белуги видно, что ее ширина и толщина составляют около 1/6 длины, поперечное сечение белуги почти круглое. Тогда нетрудно подсчитать, приняв меру полноты в одну треть, что вес такой белуги в 17 м длиною был бы около 35 т, т. е. почти 2200 пудов.
Ясно, что длина 17 м не верна, а надо 17 футов, что дает вес около 60 пу­дов. На стр. 28 указывается, что близ Нижнего поймали белугу в 40 пудов, а близ Павлова — в 50 пудов, о чем и помнили более 20 лет.
В 1862 г. в Симбирске была поймана белуга весом 90 пудов; нетрудно под­считать, что ее длина была не более 6 м.

4. Стр. 41. «В 1917 г. промыслы Сапожниковых котировались на рынке в 7 млн рублей».
Слова «котировались на рынке» делают эту фразу непонят­ной, ибо промыслы Сапожниковых никогда на рынке не котировались.

5. Стр. 48. «Карабугаз... площадью в 3000 кв. миль».
Размеры Карабугаза примерно 150 х 100 км, т. е. площадь его 15 000 кв. км. Каких миль — неиз­вестно, и число 3000 неизвестных квадратных миль ничего не выражает.
Если это географических миль, то составило бы 147 000 кв. км. Если мор­ских, то около 9000 кв. км. Если итальянских, то — около 6500 кв. км. По­этому площадь Карабугаза составляет 3000 неизвестно каких миль.

6. Стр. 61. Убитых тюленей доставляют к расшивам. «На этих судах, дли­ною в десяток, а то и в два десятка сажен и шириной до 100 саж., обделан­ных тюленей солили».
Судов в 10 или 20 сажен и шириной до 100 сажен не было, нет и не будет. Видно, что корректор ничего не понимал, что он корректировал. Такая фраза есть позор для издательства.

7. Стр. 74. «...привозят богатую тоню выловленной неводами бешенки (от 250 000 до 30 000 шт.)».
Очевидно, что одно из этих чисел неверно: или надо от 250 до 300 тысяч штук или от 25 тыс. до 30 тысяч штук.

8. Стр. 83. «У Гурьева, по сообщению Карелина (старожила, жившего там безвыездно 15 лет. — А. К.), убили белугу в 57 п.». Отсюда далеко до 2200 пудов.

[Крылов1979,с.348-349]

{Отметим, что один пуд составляет 16.3 кг, соответственно слово стопудово подразумевает 1630 кг; один фут - это 0.3048 м, это ступня где-то 45-го размера по-русски. Есть еще сажень: 1 сажень = 7 английских футов = 84 дюйма = 2,1336 метра [Указ:О системе российских мер и весов.1835].}

[117] Крылов1956: Академик Крылов А.Н. Воспоминания и очерки. - М: Издательство академии наук, 1956. - 884с.

[118] Крылов1958: Крылов А.Н. Избранные труды. - М: Издательство академии наук, 1958. - 804с.- Библиогр. осн. трудов А.Н. Крылова с.792-802. (116 назв.)

[119] Крылов1950: Крылов А.Н. Лекции о приближенных вычислениях. - 5-е изд.- М-Л.: Государственное издательство технико-теоретической литературы, 1950. - 400с.

[120] Крылов2017: Крылов А.Н. Прикладная математика и техника// Математическая составляющая. - М: Фонд "Математические этюды", 2015. С.132-143. http://book.etudes.ru/toc/technics/

§42.

Кузнецов Александр Петрович (A.P. Kuznetsov) (1954-) Заведующий базовой кафедрой динамических систем факультета нелинейных процессов СГУ. Ведущий научный сотрудник Саратовского филиала ИРЭ РАН. Д.ф.-м.н., профессор.

[121] Кузнецов2006: Кузнецов А.П. Как работают и думают физики. - М.-Ижевск: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2006. - 172с.

[122] Кузнецов2006B: Кузнецов А.П., Кузнецов С.П., Мельников Л.А. , Савин А.В. Неформальная физика.- Саратов: Изд-во "Научная книга",2006. - 104 с.

[123] Кузнецов2006C: Кузнецов А.П., Кузнецов С.П., Мельников Л.А. , Савин А.В., Шевцов В.Н. 50 олимпиадных задач по физике. - Саратов: Изд-во "Научная книга", 2006. -60с.

[124] Кузнецов2008: Кузнецов А.П., Кузнецов С.П., Савин А.В., Станкевич Н.В. Анализ в физике. Саратов: Изд-во "Научная книга", 2008. - 90с.

[125] Кузнецов2009: Кузнецов А.П., Кузнецов С.П., Савин А.В., Станкевич Н.В. Физика: от оценок к исследованию. - Москва - Ижевск: РХД, 2009. - 176с.

[126] Кузнецов2010: Кузнецов А.П. Физики тоже любят математику. - Саратов: Научная книга, 2010. - 36с.

[127] Кузнецов2015: Кузнецов А.П. Кузнецов С.П., Мельников Л.А. , Савин А.В., Шевцов В.Н. Задачи физических олимпиад. - Изд. 2-е. М.– Ижевск: Институт компьютерных исследований, 2015. - 168с.

[128] Кузнецов: Кузнецов А.П. Список публикаций (Большинство выше приведенных книг также есть в pdf-формате):
www.sgtnd.narod.ru/pabl/rus/index.htm

§43.

Ланге Виктор Николаевич (1928-)
publ.lib.ru/ARCHIVES/L/LANGE_Viktor_Nikolaevich/_Lange_V.N..html

[129] Ланге1978: Ланге В.Н. Физические парадоксы и софизмы.- Изд. третье, перераб. - М: Издательство "Просвещение",1978. - 176с. Первое изд. 1963г. Второе изд. 1967г.

[130] Ланге1983: Ланге В.Н. О скорости забывания.//Вопросы психологии. 1983. N4 с.142-145.
www.voppsy.ru/issues/1983/834/834142.htm

[131] Ланге1985: Ланге В.Н. Экспериментальные физические задачи на смекалку: Учебное руководство. - Изд. третье, перераб. и доп. - М: Наука. Главная редакция физико-математической литературы, 1985. - 128с. Первое изд. 1974г., второе изд. 1979г.

Как измерить диаметр канала однородного стеклянного капилляра от обычного медицинского термометра с помощью линейки (слишком грубой, чтобы ею можно было воспользоваться для непосредственного измерения диаметра), резиновой груши, точных весов с разновесом и капельки ртути? [Ланге1985, с. 18, 87 , задача 104]

[132] Ланге2009: Ланге В.Н. Физические опыты и наблюдения в домашней обстановке / В. Н. Ланге. - Москва : URSS : Либроком, 2009. - 227 с.

§44.

[133] Кристиан_Гриффитс2017: Кристиан Б., Гриффитс Т. Алгоритмы для жизни: Простые способы принимать верные решения. - Пер. с англ. - М: Альпина Паблишер, 2017. - 372с.
Ориг. назв.: Brian Christian, Tom Griffiths: Algoritms to live by. The computer science of human decisions. - New York: Henry Holt and Company, 2016. - 354p. Библиогр. p.315-334. Notes p.262-314. Библиогр. и Notes отсутствуют в русском издании.
Кристиан Брайан (Brian Christian)(1984-)(brianchristian.org) Журналист и писатель. Проживает в Сан-Франциско.
Гриффитс Том (Tom Griffiths) (1979-) Профессор психологии и когнитивистики Калифорнийского университета в Беркли (UC Berkeley). Проживает в Беркли (Калифорния).

Простые способы принимать верные решения. [Кристиан2017p3]
По-английски это звучит: The computer science of human decisions. (Дословно: Компьютерная наука человеческих решений).
1. Задача об оптимальной остановке. 37% (Optimal stopping)
2. Исследование и эксплуатация. Что предпочесть: проверенный ресторан или поискать что-нибудь новенького. (Explore/Exploit)
3. Сортировка. (Sorting) Облегчает поиск. Пузырьковая сортировка (Обама говорит, что ее применять не надо). Сортировка методом вставок. Как сортируют книги в библиотеках. Сортировка в спорте.
Доджсон (Льюис Кэрролл) Соревнования по теннису: верные правила присуждения призов с обоснованием ошибочности ныне действующих правил.
4. Кэширование. (Caching)
5. Планирование. (Scheduling)
6. Правило Байеса. (Bayes’s Rule) Сколько будет стоять Берлинская стена?
Закон Лапласа.
Немецкая танковая задача [Кристиан_Гриффитс2017p197]
Распределение Эрланга.
7. Переподгонка (Overfitting).
8. Лагранжева релаксация. (Relaxation) Временное снятие ограничений.
9. Случайность. (Randomness)
10. Взаимодействие в сетях. (Networking)
11. Теория игр. (Game Theory)
Дилемма заключенного [Кристиан_Гриффитс2017p229]
Трагедия общин [Кристиан_Гриффитс2017p332]
Цена анархии не превышает 4/3
[Кристиан_Гриффитс2017p331]
Тим Ругарден; Ева Тардос (Корнеллский университет) 2002.
Измени игру [Кристиан_Гриффитс2017p335].

[134] Гусинская2017: Гусинская И., зам. гл. Редактора Альпина Паблишер: Алгоритмы для жизни: Простые способы принимать верные решения
https://www.alpinabook.ru/blog/algoritmy-dlya-zhizni-prostye-sposoby-prinimat-vernye-resheniya

§45.

[135] Strauss1995: : Stephen Strauss: The Sizesaurus: From Hectares to Decibels to Calories, a Witty Compendium of Measurements. - New York: Kodansha Amer Inc, 1995. - 272p.

§46.

Гамов Георгий Антонович (1904-1968), известный и талантливый физик необычно высокого роста(204см), покинувший СССР в 1933 году:
https://ru.wikipedia.org/wiki/Гамов,_Георгий_Антонович

В [Гамов1994] привлекают внимание две истории: Игорь Тамм попал в банду Махно и его заставили считать погрешность обрезания ряда Макларена (с.22-23) и Петр Капица в 1922г. женился в Париже на дочери А.Н. Крылова, которая была без документов (с так называемым Нансеновским паспортом). Советскому послу пришлось организовать ей иранское гражданство за один день, которое перешло в советское после того, как она вышла замуж.

Сама дочь Крылова А.Н. это отрицает, и говорит, что это только было предложено советским послом:

Отчего-то Алексею Николаевичу совсем не понравилась перспектива превращения его дочери в персиянку, он страшно рассердился и поднял такую бучу в посольстве, что очень скоро все формальности были улажены.

http://ilib.mccme.ru/krylov/memories/69-2.htm

[136] Гамов1994: Гамов Дж. Моя мировая линия: Неформальная автобиография: Пер. с англ. - М.: Наука. Гл. ред. физ.-мат. лит., 1994. - 304с.
Ориг. назв.: George Gamow: My world line. An informal autobiography. - New York: The Viking Press, 1970. - 178p.

[137] Гамов2001: Гамов Г., Стерн М. Занимательная математика. — Пер. с англ. Ю.А.Данилова. - Ижевск: Научно-издательский центр «Регулярная и хаотическая динамика», 2001. - 88с.
Ориг. назв.: Gamow G., Stern M. Puzzle-math. - London: MacMillan & Co Ltd, 1958.

§47.

Гарднер Мартин (Martin Gardner)(1914-2010) Американский писатель и собиратель головоломок. Можно сказать головоломатор. Образование: Чикагский университет (бакалавр). Служба в ВМФ США. Ведущий рубрики математических игр и развлечений журнала «Scientific American». Основные произведения (канон) (ссылка на web.arhive.org):
www.kknop.com/math/MG15books.html

[138] A Martin Gardner bibliography:
www.loyalty.org/~schoen/gardner-booklist.html,
а также здесь: en.wikipedia.org/wiki/Martin_Gardner_bibliography

[139] Матвеев2018: Матвеев Михаил Вступительная статья к рассказам М.Гарднера//Иностранная литература, N 3, 2018.
http://magazines.russ.ru/inostran/2018/3/rasskazy.html

[140] Гарднер1971: Гарднер М. Математические головоломки и развлечения. - Перевод с английского. - М: Мир, 1971. - 512 с.

Глава 24. Мартышка и кокосовые орехи.
[Гарднер1971p233-239]
http://www.arbuz.uz/t_martyshka.html

Разборчивая невеста
[Гарднер1971p372-373]

§48.

Вайскопф Виктор Фредерик (Victor Frederick Weisskopf)(1908-2002)- американский физик. Родился в Вене (Австро-Венгрия). Образование: Гёттингенский университет (1931, PhD 1934 там же). В 1937 эмигрировал в США. Участник Манхэттенского проекта. Работал в Рочестерском университете, Лос-Аламосской национальной лаборатории, МТИ. Директор CERN (Швейцария) в 1961-1965 гг. C 1974г. на пенсии.
https://ru.wikipedia.org/wiki/Вайскопф,_Виктор_Фредерик

[141] Weisskopf1970: Weisskopf, Victor Frederick: Modern physics from an elementary point of view. (Report number CERN-70-08) - Geneva : CERN, 1970. - 26 p. (Lectures in the CERN Summer Vacation programme, 1969)
http://cds.cern.ch/record/274976/?ln=ru

Элементарная оценка размеров атома водорода, звезд и гор.
[Weisskopf1970]

[142] Weisskopf1986: Victor F. Weisskopf, "Search for Simplicity: Mountains, waterwaves, and leaky ceilings"// Am. J. Phys., Vol. 54, No. 2, February 1986, pp. 110 -111.
http://www.science.oregonstate.edu/~minote/wiki/lib/exe/fetch.php?media=weisskopf_simplicity_long.pdf

§49.

[143] Gleeson2007: Austin Gleeson, Department of Physics, University of Texas at Austin: Домашнее задание по физике.
https://web2.ph.utexas.edu/~gleeson/HMW1.pdf

#214 6. (a) What is the height of the National Debt in pennies stacked on top of each other.
Какова высота национального долга США, если его перевести в одноцентовые монеты и положить их друг на друга.
[Gleeson2007]

#215 (b) Suppose these pennies were distributed uniformly across the land area of the contiguous 48 states. What distance would separate each penny from its nearest neighbor?
Если эти монеты распределить равномерно по территории США, то какое расстояние будет между монетами?
[Gleeson2007]

#216 (c) How many tons of copper would be required to make these pennies?
Сколько тонн меди потребуется для изготовления этих монет?
[Gleeson2007]

{Вообще-то одноцентовые монеты изготовляюся на 97.5% из цинка с 1982г., а медь используется только для покрытия.}

{Справочные данные легко находит Google:

Толщина монеты: 1.35 мм
Диаметр: 17.91 мм
Масса: 2.5 г
Национальный долг США на 2007г. - около 9 триллионов долларов. (9*10¹²)

a. Количество одноцентовых монет в долге: 9*10¹² * 100 = 9*10¹⁴ штук.

Высота национального долга США составит:

1.35 мм * 9*10¹² * 100 = 12.1* 10¹⁴ мм = 1.2* 10¹⁵ мм = 1.2* 10¹² м = 1.2*10⁹ км = 1.2 млрд. км.

Это соответствует минимальному расстоянию от Земли до Сатурна (1.2 млрд. км, среднее - 1.28 млрд. км)

b. Площадь США составляет 9.8 млн. кв. км = 10¹³ кв. м (Приблизительно)

На 1 кв. метр поверхности США приходится, соответственно 1200 монет диаметром практически 18 мм.

На одну монету приходится 10000/1200 = 8.3 кв. см.

Саму монету можно разместить в квадрате 1.8*1.8 см = 3.24 кв.см.

Здесь и далее рассматривается равномерное размещение по квадратам. Мы не будем прибегать к специальным ухищрениям и увеличивать количество монет, которые можно разместить на данной площади.

Как уже отмечалось, на одну монету приходится 8.3 кв. см или квадрат со стороной почти 2.9 см

Если малый квадрат разместить в большом, то между монетами будет удвоенная разность сторон квадратов: 2*(2.9-1.8) = 2.2 см

Таким образом, если весь государственный долг США (на 2007г.) перевести в одноцентовые монеты и равномерно раскидать по территории США, то между монетами соседними монетами останется промежуток в 2 см.

c. Вес этих монет(конечно правильно говорить "масса") составит:

2.5 г * 9*10¹²*100 = 2.25*10¹⁵ г = 2.25*10⁹ тонн

или около 2 млрд. тонн.

Производство цинка в мире в 2009 году, к примеру, составило 11.2 млн. тонн.}

§50.

[144] 4brain.ru:
https://4brain.ru/blog/решение-нестандартных-задач-ферми

#217 Задача 1. Найдите, сколько вам потребуется написать страниц текста, для того, чтобы читать его вслух в течение одного часа.
[4brain.ru]

{Читать вслух в течении часа? Гораздо проще определить, сколько страниц можно прочитать за минуту. (или минут на страницу) Факторов много: размер шрифта, интервал, наличие иллюстраций, темп оратора. Допустим, можно прочитать страницу за две минуты, тогда за час будет 30 страниц }

#218 Задача 2. Сколько потребуется бензина, чтобы проехать от Калининграда до Владивостока на Ладе Калина.
[4brain.ru]

{ Мы должны узнать расстояние от Владивостока до Калининграда с помощью навигатора (Google и Yandex) и средний расход топлива Лады Калины.
Yandex показал 10 тыс. км, 5.5 дней, Google - 9909 км и 2000 часов (часы неправильно, или он время перехода границы считает?) Расход топлива литров 7 на трассе и 10 в городе. итого получится чуть меньше 1.5 тыс. литров бензина. Бак Лады Калины - 50л. (заправится придется раз 30).
Теперь поговорим о стоимости поездки: 1 л бензина стоит рублей 40 (плюс-минус) Тогда полторы тысячи литров обойдутся в 60 тыс. руб. Билет на самолет Аэрофлота стоит 18810 руб. Перелет займет 16.5 часов. То есть преимущества путешествия на автомобиле сомнительны, и только при наличии нескольких человек (или груза) Но с точке зрения познавательной данное путешествие может быть интересным.
Расходы автомобиля на 1000 км пути включают:
- бензин,
- амортизация автомобиля,
- страховка,
- плата за дорогу, зеленая карта (та область дороги, где обычная страховка не действует),
- труд водителя}

#219 Задача 3. Сколько коробок с пиццей может поместиться в Daewoo Matiz с водителем.
[4brain.ru]

[145] 4brain.ru/Примеры:
https://4brain.ru/blog/примеры-нестандартных-задач-ферми

#220 Задача 1. Колесо
Сколько молекул резины стирается с покрышки легкового автомобиля за один оборот колеса?
[4brain.ru]

#221 Задача 2. Копилка
Сколько рублевых монет поместится в свинью-копилку приблизительным диаметром 30 сантиметров?
[4brain.ru]

#222 Задача 3. Клавиатура
Посчитайте в течение 30 секунд, сколько клавиш на клавиатуре вашего ноутбука.
[4brain.ru]

#223 Задача 4. Затмение
На каком расстоянии от глаза и от солнца должен быть круг диаметром 100 метров, чтобы получилось точное солнечное затмение?
[4brain.ru]

§51.

[146] Romack2000: Barbara Romack (Kaneland Elementary School, Elburn, IL): Fermi Problems - From Pianos to m&m's. 2000.
https://ed.fnal.gov/trc_new/sciencelines_online/fall99/activity_insert.html

RESOURCES

Burns, Marilyn, The Book of Think, Little, Brown and Company, Boston, 1976. (ISBN 0-316-11742-0)

Burns, Marilyn, The I Hate Mathematics! Book, Little, Brown and Company, Boston, 1975. (ISBN 0-316-11740-4)

Burns, Marilyn, Math for Smarty Pants, Little, Brown and Company, Boston, 1982. (ISBN 0-316-11738-2)

Schwartz, David M., How Much Is a Million?, Lothrop, Lee & Shepard Books, New York, 1985. (ISBN 0-688-04049-7)

§52.

[147] Stewart.FermiQuestions: Lori Stewart: Fermi Questions.
https://www.education.com/activity/article/Fermi_middle

Вопросы Ферми для детей:

#224 Сколько пиццерий в вашем штате?
[Stewart]

#225 Сколько машин проезжает по вашей улице за день? А за год?
[Stewart]

#226 Сколько времени за год все ученики в вашей школе тратят на решение тестов?
[Stewart]

§53.

[148] Barahmeh_Hamadp2017: Haytham Mousa Barahmeh (Abu Dhabi Education Council), Adwan Mohammad Bani Hamad (Abu Dhabi Education Council), Dr. Nabeel Mousa Barahmeh (Yarmouk University): The Effect of Fermi Questions in the Development of Science Processes Skills in Physics among Jordanian Ninth Graders.// Journal of Education and Practice, Vol.8, No.3, 2017. - 9p. ( References p.192-194. 45 названий).
https://files.eric.ed.gov/fulltext/EJ1131587.pdf

§54.

[149] tproger.ru.2016: Что могут спросить на собеседовании: подборка задач Ферми
https://tproger.ru/problems/fermi

#227 Сколько флаконов шампуня производится в мире за год?
[tproger.ru.2016]

#228 Cколько мячей для гольфа войдет в школьный автобус?
[tproger.ru.2016]

#229 Сколько насечек на ребре четвертака — монеты в 25 центов?
[tproger.ru.2016]

#230 Сколько будет 2 в 64 степени?
[tproger.ru.2016]

#231 Сколько туалетной бумаги потребуется, чтобы покрыть ею весь штат?
[tproger.ru.2016]

#232 Сколько молекул резины стираются с шины автомобильного колеса при каждом его обороте?
[tproger.ru.2016]

{В данном случае корректно говорится о молекулах резины}

#233 Cколько денег понадобится на мытье всех окон в Сиэтле?
[tproger.ru.2016]

Еще пачка задач без решения:

#234 Сколько автозаправок в Соединённых Штатах? (Этот вопрос был задан в General Motors.)
[tproger.ru.2016]

#235 Сколько мусорщиков работает в Калифорнии? (Apple)
[tproger.ru.2016]

#236 Оцените число такси в Нью-Йорке. (KPMG)
[tproger.ru.2016]

#237 Сколько шаров для гольфа нужно, чтобы заполнить ими площадь стадиона? (JP Morgan Chase)
[tproger.ru.2016]

#238 Сколько пылесосов производится в год? (Google)
[tproger.ru.2016]

В статье использовались материалы с сайта 4brain.ru, книги «Действительно ли вы достаточно умны, чтобы работать в Google?», а также лекции Постникова С.Н.

§55.

[150] Паньшин2016: Паньшин И.: Вопросы Ферми и здравые ответы на дурацкие задачи.
https://newtonew.com/science/fermi-questions

#239 Вопрос: сколько флаконов шампуня производится в мире за год?
[Паньшин2016]

#240 Вопрос: у вас есть стопка десятирублёвых монет высотой с Эйфелеву башню. Сможете ли вы уместить эти монеты в среднестатистическую комнату?
[Паньшин2016]

#241 Вопрос: сколько настройщиков пианино в Чикаго?
[Паньшин2016]

{Классическая вторая задача Ферми}

#242 Сколько коров в Канаде?
[Паньшин2016]

#243 Оцените количество автозаправок в России.
[Паньшин2016]

#244 Сколько потребуется рулонов туалетной бумаги, чтобы покрыть ею всю Москву и сколько на это необходимо денежных средств?
[Паньшин2016]

#245 Сколько людей ежегодно оканчивают университет?
[Паньшин2016]

#246 Сколько насечек на 5-тирублевой монете?
[Паньшин2016]

#247 Сколько каждый год выпускается книг?
[Паньшин2016]

[151] Паньшин2015: Паньшин И. Нехитрые приёмы манипуляции данными.
https://newtonew.com/science/how-to-lie-with-data

§56.

[152] Полякова2012: Полякова С.В. Занятие на тему "Решение нестандартных задач" (Математика.Внеклассная работа.) 24.01.2012
http://web.archive.org/web/20161101095223/ http://festival.1september.ru/articles/609683

#248 Вы плывете на яхте по Тихому океану. Штурман сообщает, что сейчас вы находитесь над самым глубоким местом на земле - Марианской впадиной. Именно в это время неловкий гость случайно роняет пушечное ядро массой 5,5 кг за борт. Через какое время ядро достигнет дна?
[Полякова2012]

{Как и в задачах о парашютистах выясняется, что ядро падает совсем не с ускорением, как можно подумать, а равномерно (кроме, конечно, первого момента, когда выходит на режим падения). Глубину Марианской впадины несложно найти в интернете, а скорость погружения ядра - 3 м/с приводится без обоснования. Таким образом, время погружения составит около 1 часа. 36666 сек указаны ошибочно.}

§57.

[153] Radistao.habrahabr.ru.2013: Radistao: Готовы ли мы все перейти на электрокары (задача Ферми)
https://habrahabr.ru/post/177621

{Если перейти полностью на электромобили, хватит ли электроэнергии?}

[154] Подольский2013: Подольский А. Электрокары. Борьба за экологию или модная мировая "фишка"?
https://www.drive2.ru/b/1998988

§58.

Сколько электрической энергии требуется на поддержание функционирования биткойна?

Если мы все перейдем на биткойны, не случится ли энергетического коллапса?

Одна транзакция биткойна требует 200 кВт*ч электроэнергии. Не ватт, а киловатт. Это соответствует 24-часовой работе небольшой сауны в 8 кВт. Всего в мире выработано в 2016 году около 25 триллионов кВт*ч электроэнергии. Это за год. Можно провести около 10 млрд. транзакций. (на 6 млрд. человек) Стоимость одной транзакции, если взять стоимость одного квт*ч в 5 руб., составит 1000 руб. (около 15 долларов).

Может быть процесс майнинга надо совместить с работой электрообогревателей?

[155] Опря2017: Сколько электроэнергии требуется на одну транзакцию биткоина?
https://bits.media/news/skolko-elektroenergii-trebuetsya-na-odnu-tranzaktsiyu-bitkoina

[156] Weese2017: Leo Weese: Bitcoin mining and energy consumption, 8.12.2017.
https://blog.bitcoin.org.hk/bitcoin-mining-and-energy-consumption-4526d4b56186
Русский перевод:
Биткоин-майнинг и потребление энергии
https://vc.ru/30588-bitkoin-mayning-i-potreblenie-energii

Расчет мирового потребления энергии на биткойны через мощность используемого оборудования.

[157] СтатистикаМЭА2017: Статистика Международного энергетического агентства:
https://www.iea.org/publications/freepublications/publication/KeyWorld2017.pdf

[158] Золотов2018: Золотов Е. Съест ли биткойн всё электричество? И сможет ли Ethereum это исправить?//Компьютерра, 10.05.2018
https://www.computerra.ru/229056/sest-li-bitkojn-vsyo-elektrichestvo-i-smozhet-li-ethereum-eto-ispravit

§59.

[159] Ушбаев2013: Ануар Ушбаев: Выбор следующего президента как задача Ферми.//Anuar D. Ushbayev's blog, 4.06.2015
https://anuarushbayev.wordpress.com/2015/06/04/choice-of-next-president-as-a-fermi-problem

§60.

[160] Чернов2015: Чернов Дмитрий: Для ботаников: Сколько атомов резины стирается с колеса за один оборот?//23.01.2015
http://www.4ernov.ru/2015/01/blog-post_23.html

#249 В Саратове проживает около 830 000 человек, сколько в нем содержится школьных учреждений?
[Чернов2015]

#250 Сколько коробок с пицей поместится в багажник Deo Matiz?
[Чернов2015]

#251 Сколько пачек масла понадобится для приготовления бутербродов в детском саду?
[Чернов2015]

#252 Сколько атомов резины стирается с колеса легкового автомобиля за один оборот?
[Чернов2015]

§61.

[161] Макдауэлл2016: Макдауэлл, Гейл Лакман: Карьера программиста. Решения и ответы 189 тестовых заданий из собеседований в крупнейших IT-компаниях. - 6-е изд. - СПб: Питер, 2016. - 688с. - Тираж 1500. Доп. глава с подсказками на сайте издательства.
Ориг. назв: Gayle Laakmann Mcdowell (1982-): Cracking the Coding Interview: 189 Programming Questions And Solutions.
Подсказки:
http://storage.piter.com/upload/new_folder/978549602154/ Kariera%20programmista_chXIII.pdf

G. L.Mcdowell - Founder and CEO CareerCup.com. Сайт автора:
http://www.gayle.com

Задачи для собеседований: всего 10.[Макдауэлл2016p117-119].

#253 1. Есть 20 баночек с таблетками. В 19 баночках лежат таблетки весом 1г , а в одной - весом 1.1 г. Даны весы, показывающие точный вес. Как за одно взвешивание найти банку с тяжелыми таблетками?
[Макдауэлл2016]

{Нумеруем баночки от 1 до 20. Берем из первой баночки 1 таблетку, из второй - 2, из третьей - 3 и т.д. Хочется верить, что таблеток в каждой баночке больше 20, иначе ничего не получится. Кладем все эти таблетки на весы. Весы покажут целый вес 1+2+3...+20 = 210г плюс число кратное 0.1 г ( от 0.1 до 2.0) По этому числу и найдем баночку с тяжелыми таблетками.

Отметим, что решение неустойчиво в случае, если баночка с тяжелыми таблетками не одна.

Вопрос, как найти сумму 1+2+3.., рассматривается в отдельной секции, самый простой способ сложить на калькуляторе. А можно прибегнуть к методу пятилетнего Гаусса и умножить 21 на 10.}

#254 2.Что лучше: попасть в баскетбольное кольцо за одну попытку или два раза из трех?
[Паундстоун2012p252-256].

#255 3. Вырезаны два противоположных угла на шахматной доске, можно ли закрыть всю доску костью домино на две клетки.
[Шеллинг2016p70-71]
[Паундстоун.Google, с.130]

#256 4. Муравьи ползут по треугольнику.
[Макдауэлл2016]

#257 5. Как отмерить 4 л воды с помощью кувшинов 3 и 5.
[Макдауэлл2016]

#258 6. Вывоз голубоглазых людей с острова.
[Макдауэлл2016]

#259 7. Какое соотношение полов, если в семьях рожают мальчиков до первой девочки (обычно наборот)
[Гамов_Стернp20]

#260 8. Как сбрасывать яйца со стоэтажного здания.
[Паундстоун2012p166-177]

#261 9. 100 закрытых замков с переключением.
[Макдауэлл2016]

#262 : 10. Имеется 1000 бутылок лимонада, ровно одна из которых отравлена. Также у вас есть 10 тестовых полосок для обнаружения яда. Даже одна капля яда окрашивает полоску и делает ее непригодной для дальнейшего использования. На тестовую полоску можно одновременно нанести любое количество капель, и одна полоска может использоваться сколько угодно раз (при условии, что все пробы были отрицательными). Однако вы можете проводить испытания не чаще одного раза в день, а до получения результата с момента проведения проходит 7 дней. Как найти отравленную бутылку за минимальное количество дней?
[Макдауэлл2016]

Есть очень красивое, но нежизненное решение. Красивое, поскольку нужно произвести только одно измерение. Все бутылки нумеруются в двоичной системе. Раскладываются 10 тестовых полосок. Они тоже нумеруются. Берется каждая бутылка и из нее капают только на те полоски, которые имеют единицу в номере бутылки.

Например:
0100000001 - номер бутылки, капаем на вторую полоску и на десятую.

Результат мы увидим через семь дней. Покрасневшие полоски укажут на номер бутылки.

А нежизненное решение потому, что если отравленная бутылка не одна, мы ничего не увидим, а наоборот выкинем хорошую бутылку, а отравленные оставим для дальнейшего употребления.

Может быть стоит кодировать бутылки помехоустойчивым кодом?

§62.

Full Moon Silhouettes from Mark Gee on Vimeo.

#263 С какого расстояния сделано это фото? [Сурдин2017p33]

{ Луна видна под углом в полградуса. Расстояние до Луны 380 тыс. км. Диаметр Луны 3400 км. На фото на диск Луны по горизонтали помещается около 11 человеческих роста. 1.75*11 = около 20 м. Разделив диаметр Луны на 20 м получим 170 тыс. раз. В такое количество раз люди ближе к фотографу, чем Луна. Разделив 380 тыс. км. на 170 тыс., получим примерно 2.2 км. Сам фотограф пишет о расстоянии 2.1 км

Угол в поградуса и не понадобился. Зная его, можно по диаметру Луны определить расстояние до нее, или наоборот, по расстоянию до Луны определить ее размер.

Другой способ. Предмет, размером в 1 м, виден с 6 метров под углом в 10 градусов. Под углом в 1 градус этот же предмет виден с 60 м. Под углом в полградуса, как Луна, со 120 м. У нас предмет в 20 метров (11 человеческих ростов). 120*20 = 2400 м.

Конечно, погрешность в 14% (2.4/2.1) достаточно велика, но можно вспомнить, что угловой размер Луны не 30 минут (полградуса) точно, а от 29′24″ до 33′40″.}

Ниже приведен ответ из [Сурдин2017p156]:

[162] Сурдин2017: Сурдин В.Г. Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике. - М: Альпина нон-фикшн, 2017. - 242с. - Тираж 4000.

[163] Gee2013: Фотограф Mark Gee.
http://theartofnight.com/2013/01/full-moon-silhouettes

[164] Золотухин2015: Золотухин Александр на русском языке: Силуэты в полнолуние:
https://alexandrz.com/full-moon-silhouettes

§63.

[165] Mondalek_Nisen2013: Alexandra Mondalek and Max Nisen: 13 Brain-Melting Questions That Companies Ask During Interviews// 10.06.2013
http://www.businessinsider.com/answers-to-interview-brainteasers-2013-7

[166] Ideanomics2013: На русском языке: Самые каверзные вопросы на собеседованиях в самые крутые компании. 11 задачек, от которых расплавится мозг.
https://ideanomics.ru/articles/1100

#264 1. Сколько автозаправок в США?
[Ideanomics2013]

#265 2. Как вы будете тестировать калькулятор?
[Ideanomics2013]

#266 3. Сколько мячей для гольфа во Флориде.
[Ideanomics2013]

#267 4. Сколько фонарей в Нью-Йорке?
[Ideanomics2013]

#268 5. Сколько стоит груша, если яблоко стоит...
[Ideanomics2013]

#269 6. Оцените спрос на пластиковые пакеты в США.
[Ideanomics2013]

#270 7. Опишите интернет для человека после 30-летней комы.
[Ideanomics2013]

#271 8. Что более полезно для оценки числа людей, которые работают в 30-этажном здании:
- Число машин на парковке.
- Число людей на ланче в кафетерии.
- Число людей на 11 этаже.
[Ideanomics2013]

Which of these pieces of information would be most useful in estimating the number of people who work in a 30-story building?
a. The number of cars in the parking lot.
b. The number of people eating lunch in the cafeteria.
c. The number of people on the 11th floor.

#272 9. Сколько приносит Starbacks на Таймс-сквер в год?
[Ideanomics2013]

#273 10. Бактерии размножаются в чашке Петри...
[Ideanomics2013]

{Если бактерии делятся каждую минуту и размножаются 1 час, то каких размеров должна быть чашка Петри...?}

#274 11. Сколько картофеля в килограммах продает Макдоналдс в год в Великобритании.
[Ideanomics2013]

#275 12. Какова вероятность, что пять человек сядут за круглый стол в порядке возрастания/убывания?
[Ideanomics2013]

#276 13. 12 монет и одна легче или тяжелее. Как ее найти в три взвешивания?
[Ideanomics2013]

§64.

[167] Долбичкина2019: Долбичкина А: Метод Ферми: как научиться измерять неизвестное//lifehacker.ru,15.01.2019
https://lifehacker.ru/metod-fermi

§65.

[168] Ногалес2014: Ногалес Кирилл: Приближённые вычисления в жизненных ситуациях:
https://4brain.ru/blog/приближённые-вычисления

§66.

[169] Шустов2013: Под ред. Шустова Б.М., Рыхловой Л.В. Астероидно-кометная опасность: вчера, сегодня, завтра. - М: ФИЗМАТЛИТ, 2013. - 384с.
http://militaryrussia.ru/forum/download/file.php?id=38471

[170] Шустов2012: Шустов Б.М. «Астероидно-кометная опасность» 19.12.2012. «Трибуна ученого» в Московском Планетарии:

[171] Финкельштейн2007: Финкельштейн А. (Институт прикладной астрономии РАН, Санкт-Петербург) Астероиды угрожают Земле//Наука и жизнь, N 10, 2007.
https://www.nkj.ru/archive/articles/11835

[172] Лаговский2018: Лаговский Владимир: Астероид пробил в Гренландии дыру диаметром в 31 км. Ученые обнаружили гигантский ударный кратер подо льдом острова//www.crimea.kp.ru, 16.11.2018
https://www.crimea.kp.ru/daily/26908/3954317
Источник:
Kurt H. Kjær and others: A large impact crater beneath Hiawatha Glacier in northwest Greenland//Science Advances 14 Nov 2018: Vol. 4, no. 11, eaar8173
DOI: 10.1126/sciadv.aar8173
https://advances.sciencemag.org/content/4/11/eaar8173

[173] Шувалов2017: Шувалов В.В., Светцов В.В., Артемьева Н.А., Трубецкая И.А., Попова О.П., Глазачев Д.О. Астероид Апофис – оценка опасных последствий ударов подобных тел//Астрономический вестник. Выпуск №1. 2017. Том 51.с.51-66.
https://www.libnauka.ru/item.php?doi=10.7868/S0320930X17010042

Сидоров М.: Версия №1: Землю может уничтожить астероид
https://rg.ru/2012/12/06/apocalypse-1asteroid-site.html

§67.

Лобановский Юрий Иоасафович. Расчеты по метеоритам.
http://www.synerjetics.ru

[174] Лобановский:Челябинский метеороид.2016: Лобановский Ю. И. Челябинский метеороид: критика источников и обоснование выводов//
http://www.synerjetics.ru/article/springs_critique.htm

[175] Лобановский:Тунгусский метеороид.2019: Лобановский Ю. И. О направлении полета и наклоне траектории Тунгусского метеороида//
http://www.synerjetics.ru/article/flight_direction.htm

§68.

[176] Crack2014: Crack, Timothy Falcon: Heard on the Street: Quantitative Questions from Wall Street Job Interviews.- Revised 15th Edition. 2014. www.InvestmentBankingJoInterviews.com - 335p. References p.309-320. (207 titles)

#277 1.4. What is the sum of the integers from 1 to 100? [Crack2014p12]
Какова сумма целых от 1 до 100?

{Задача восходит к Гауссу.}

#278 5.5.1 Tell me a joke. [Crack2014p62]
Расскажите шутку.

#279 5.5.5. If a cannonball is dropped in the deepest part of the Earth’s oceans, how long will it take to reach the ocean floor?[Crack2014p62]
Если бросить пушечное ядро в воду в глубочайшем месте из земных океанов, через сколько времени оно достигнет дна?

#280 5.5.6. How many ping-pong balls can you fit in a jumbo jet (e.g. Boeing 747)? [Crack2014p62]
Сколько шариков для пинг-понга можно набить в реактивный лайнер? (например, Boeing 747)?

#281 5.5.7. How many McDonald’s fast food outlets are there in the US? [Crack2014p62]
Сколько Макдональдсов в США?

#282 5.5.8. How many windows are in this building? [Crack2014p62]
Сколько окон в этом здании?

#283 5.5.9. How many flight attendants does {name an airline} have? [Crack2014p62]
Сколько стюардесс в такой-то авиакомпании? {стюарды тоже относятся в данную категорию}.

#284 5.5.10. How many gas station are there in the USA? What about the UK?[Crack2014p62]
Сколько автозаправок в США? А как насчет Великобритании?

#285 5.5.13. How many elevators (lifts) are there in the USA?[Crack2014p62]
Сколько лифтов в США?

#286 5.5.15 I toss a coin 100 times and get 100 heads in a row. What is the probability that the next outcome will be a head? [Crack2014p63]
Я бросил монетку 100 раз и получил 100 орлов. Какова вероятность, что в 101 раз выпадет тоже орел?

#287 5.5.16 How would you move Mount Fuji? [Crack2014p63]
Как передвинуть гору Фиджи.

{Паундстоун подробно рассматривает данный вопрос.}

#288 5.5.17. How do you weight a jet airplane without using scales? [Crack2014p63]
Как взвесить реактивный самолет, не используя весов?

#289 5.5.18. You have a five-gallon jar and three-gallon jar. You have as much water as you want. How do you put exactly four gallons into the five-gallon container? [Crack2014p63]
У вас два кувшина в три и пять галлонов воды. И бесконечное количество воды. Как получить точно четыре галлона воды в пятигаллонном кувшине?

#290 5.5.19. Estimate the annual demand for car batteries?[Crack2014p63]
Оцените годовой спрос на аккумуляторные батареи для автомобилей.

#291 5.5.20. What would you estimate to be the size of the racquetball market in the USA? [Crack2014p63]
Оцените бадмингтонный рынок в США.

#292 5.5.21. You are to build a plant for Coors to serve all beer customers in the state of Ohio. How large would you build it? That is, specifically how many cans (of the new wide-mouth variety) do you anticipate being demanded for the year?[Crack2014p63]
Вы должны построить пивной завод, чтобы он обслуживал всех потребителей определенной марки в штате Огайо. Каких он должен быть размеров? Определите, какое количество пивных банок потребуется производить в год.

#293 5.5.23. Explain why airplane can fly.[Crack2014p63]
Объясните, почему самолеты могут летать.

#294 5.5.24. How many fish are there in the Earth’s ocean? [Crack2014p63]
Сколько рыбы в море?

#295 5.2.25. How many barbers are there in Chicago? [Crack2014p63]
Сколько парикмахеров в Чикаго?

#296 5.5.26 What is sqrt(204 000)? [Crack2014p63]
Корень квадратный из 204 тыс.

{Возьмите калькулятор - и ответ в ваших руках. Если же без калькулятора, то можно быстро определить, что это корень из 20, умноженный на 100. Корень из 20 больше 4-х (16) и меньше 5-ти (25), т.е. где-то 4.5. Умножаем на 100 и получаем 450. (Калькулятор, кстати, даст близкое значение (451.6).}

#297 5.5.27. What is one percent of 1 000 000? [Crack2014,p.63]
Сколько будет один процент из миллиона?

{1% - это одна сотая, следовательно 10 тыс.}

#298 5.5.28. Finally, why are manhole covers round? [Crack2014,p.63]
Наконец, почему крышки люков круглые?

§69.

[177] ScienceOlympics2018: Science Olympic// The University of Western Ontario, Department of Physics and Astronomy, 2001,2018.
http://www.physics.uwo.ca/science_olympics/events/puzzles/fermi_questions.html

274 задачи Ферми

§70.

[178] deCabezón2014: Эдуардо Саэнц де Кабесон(Eduardo Sáenz de Cabezón) Математика - это навсегда. Выступление на TED. Буэнос-Айрес, Аргентина.2014. Есть русские субтитры.

https://www.ted.com/talks/eduardo_saenz_de_cabezon_math_is_forever?language=ru

...удивляет то, что если взять лист бумаги в 0,1 миллиметр толщиной — обычная толщина бумаги — и, если бы он был достаточно большим, сложить его 50 раз, то толщина такой стопки достигнет расстояния от Земли до Солнца. Твоя интуиция говорит, что это невозможно. Сделай расчёт, и убедишься в этом сам. Вот для чего нужна математика.
[на отметке 3:43]

{Ты делаешь расчет и убеждаешься, что бумага до Солнца-то и не дотянется. Чуть-чуть не хватит. (112.5 млн. км). Надо или бумагу взять потолще, либо сложить 51 раз. Я был далеко не первый, кто это заметил, даже комментарий подобный размещен.

Расчет можно произвести тремя способами:
Длина сложенного листа бумаги составит, теоретически: 0.1 мм * 2⁵⁰

2⁵⁰ степени можно вычислить взяв натуральный логарифм от 2, умножить его на 50 и применить функцию e^x: 2⁵⁰= 1.125*10¹⁵.

Можно взять десятичный логарифм, умножить на 50 и возвести в 10^x. Результат будет тот же.

Можно считать, что 2¹⁰ = 1000, тогда 2⁵⁰ = 10¹⁵.
Поскольку 2¹⁰ = 1024, что больше 1000 на 1.024 или 2.4%, то можно произвести коррекцию результата, умножив на 1.024⁵ = 1.125 (перемножив пять раз).
Мы опять пришли к тому же результату.

Теперь осталось умножить на 0.1мм = 10^-4 м и получить окончательный результат: 1.125*10¹¹ м = 112.5 млн. км.

Поскольку в школьной астрономии учат, что до Солнца 150 млн. км, то лист бумаги, сложенный 50 раз, до Солнца не достанет. }

§71.

[179] Бердов2012: Бердов Павел: Быстрое вычисление квадратных корней//
https://www.youtube.com/watch?v=UvKJGxvlDt4

Уметь правильно и быстро оценивать и ощущать значение квадратного корня - очень важно. К недостаткам данного метода можно отнести то, что он заточен под целые числа, что больше годится для школьной программы, а не для реальной деятельности.

§72.

Капица Пётр Леонидович (Pyotr Leonidovich Kapitsa или Peter Kapitza)(1894-1984)- советский физик. Работы в области низких температур. Нобелевская премия по физике 1978г. (НПФ-1978). Академик АН СССР. Член Лондонского Королевского общества (Fellow of the Royal Society). Основал Институт физических проблем в 1934г. (Постановление СНК СССР от 23.12.1934).

1934. Постановление об организации института Физических проблем
http://kapitza.ras.ru/arhiv/doc/1934.jpg

[180] Капица1966: Капица П.Л. Физические задачи. М.: Знание, 1966. 16 с.
http://vivovoco.astronet.ru/VV/PAPERS/KAPITZA/KAPQUEST.HTM

[181] Капица1968: Капица П.Л. Понимаете ли вы физику? - М: Издательство «Знание», 1968. - 96с.

Напечатанные в этом сборнике задачи были составлены мной для студентов Московского Физико-технического института, когда в 1947-1949 гг. я там читал курс общей физики. В этот сборник вошли также задачи, которые давались на экзаменах при поступлении в аспирантуру Института физических проблем Академии наук СССР. Эти задачи собрали вместе и подготовили к печати студенты физтеха, недавно окончившие институт, Л.Г. Асламазов и И.Ш. Слободецкий [Капица.Задачи.1968,с.3].

Приведены ответы, указания и решения.

[182] Капица1981: Капица П.Л.Капица П.Л. Эксперимент, теория, практика: Статьи, выступления. - М: Наука, 1981. -496с. - Библиография трудов П.Л.Капицы с.485-489 (78 назв.)

[183] Капица1974: Капица П. Л. Карманный справочник физика-экспериментатора (цитатник). — М., 1974.- Машинопись. http://mipt.ru/upload/medialibrary/b56/kapitza120.pdf

Шли трое по берегу реки. Один говорит: "На том берегу что-то любопытное". Другой присмотрелся и сказал: "Это кошелек. Как бы его достать?" У третьего оказалась дрессированная собака, которая и принесла кошелек. Как поделить деньги?

Комментарий: {Второй, наверное, сказал: "Я знаю десять способов достать кошелек."}

[184] Капица_Ландау2017: Капица, П.Л., Ландау, Л.Д. Физические основы механики (как изучали физику на ФТФ МГУ в 1947г.) / ред. В.С.Булыгин. — М. : МФТИ, 2017. — 219 с.
https://mipt.ru/education/chair/physics/S_I/method/FTF_Meh1.pdf

[185] Рубинин_Капица2007: Рубинин П.Е.: Капица в моих старых записных книжках//Природа. N 7. 2007.
http://vivovoco.astronet.ru/VV/JOURNAL/NATURE/06_07/RUBIKAP.HTM

[186] Добровольский_Капица2007: Добровольский Е.Н. Почерк Капицы. (Люди Советской России). - М: Советская Россия, 1968. - 177 с., 19 л. ил.

§73.

Тест Шейна Фредерика/ The Cognitive Reflection Test (CRT)

Shane Frederick (Фредерик Шейн) (1968-) (Фредерик - это фамилия) The Yale School of Management:
https://som.yale.edu/faculty/shane-frederick
Ранее: Massachusetts Institute of Technology.
https://en.wikipedia.org/wiki/Shane_Frederick

[187] Frederick2005: Shane Frederick: Cognitive Reflection and Decision Making// Journal of Economic Perspectives. Volume 19, Number 4—Fall 2005. Pages 25–42. Библиогр. c.41-117(1647 назв.){Библиография растет в интерактивном режиме не по дням, а по часам.}
https://pubs.aeaweb.org/doi/pdfplus/10.1257/089533005775196732

Вторичные источники:

[188] Pochin2019: Courtney Pochin: World's shortest IQ test only has three questions - but 80 percent fail it.
https://www.mirror.co.uk/news/weird-news/worlds-shortest-iq-test-only-18510848

[189] rbc.ru.2019: В США придумали IQ-тест из трех вопросов
https://www.rbc.ru/rbcfreenews/5d3699029a7947e162d91ffb?from=newsfeed

The Cognitive Reflection Test (CRT)

#299 (1) A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost? _____ cents
Бита и мяч вместе стоят 1.10 доллара. Бита стоит на 1 доллар дороже мяча. Сколько центов стоит мяч?
[Frederick2005]

{В русском переводе биту часто заменяют на теннисную ракетку.
Если вы подумали, что мяч стоит 10 центов, то бита стоит 1.10, а вместе они стоят 1.20, что противоречит условию задачи.}

#300 (2) If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets? _____ minutes
Пять машин производят за 5 минут 5 вещей. Сколько времени потребуется 100 машинам, чтобы произвести 100 вещей?
[Frederick2005]

{Понятно, что хочется сказать 100 минут. Но это неправильно. Одна машина производит одну вещь. А занимает это 5 минут.}

#301 (3) In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake? _____ days
На озере растут кувшинки. Каждый день их количество удваивается. Через 48 дней они закроют все озеро. За сколько дней они закроют половину?
[Frederick2005]

{Число озер, в которых кувшинки смогут удваиваться 48 раз, сильно ограничено. Простая оценка показывает, что площадь озера должна быть больше 100 тыс. кв. км. Таких озер немного. А чтобы закрыть половину озера хватит и последнего дня.}

Другие варианты подобных вопросов:

#302 Обед с чаевыми обошелся в 1100 рублей. Обед стоил на 1000 рублей больше, чем чаевые. Каков размер чаевых? 
[Белянин2018_16:48].

#303 З кофейных автомата делают З чашки кофе за З минуты. За  сколько времени 24 таких же автомата сделают 24 чашки кофе? 
[Белянин2018_16:52]

[190] Белянин2018: Белянин Алексей: Поведенческая экономика - наука о человеке (и для человека?)
https://www.youtube.com/watch?v=_l6YbMr1iqc&t=1006s

#304 Если пять кошек ловят пять мышей за пять минут, то сколько времени нужно одной кошке, чтобы поймать одну мышку?
https://bloggood.ru/raznye-temy/smeshnye-logicheskie-zagadki-s-podvoxom-otgadki-prilagayutsya.html

«Трешов [прим. Нильс Трешов - ректор университета Осло] ... любил подшучивать над пристрастием Абеля к математике... «Однажды он сказал Нильсу Абелю, - рассказывает в своих воспоминаниях жена Трешова,
- «Послушай, Нильс, если полторы селедки стоят полтора пенни, сколько должна стоить дюжина?»
- «Восемнадцать», - ответил Нильс Абель. Трешов расхохотался, потирая руки от удовольствия».
Источник: О. Оре. Замечательный математик Нильс Хенрик Абель. - М.: Государственное изд-во физико-математической лит-ры, 1961. - с. 273-274
https://mathlife.ru/news/niels_henrik_abel

{А почему не 12?}

«Трое мужчин могут покрасить три забора за три часа. Сколько времени потребуется, чтобы один человек покрасил один забор?»
https://mathlife.ru/news/niels_henrik_abel

«Полторы курицы за полтора дня несут полтора яйца. Сколько яиц снесут две курицы за три дня?»
https://mathlife.ru/news/niels_henrik_abel

"Бутылка и пробка стоят 10 копеек. Бутылка на 8 копеек дороже пробки. Сколько стоит бутылка?"
[Носов.ВитяМалеев.1951,с.182]

[191] Носов1951: Носов Н.Н. Витя Малеев в школе и дома.//Новый мир. N6. 1951. с.109-190.
http://lib.novymirjournal.ru/bookreader/journal.php?guid=F0777B22-D3C1-ED49-B782-4F8CF3414F3E#page/1/mode/1up

Автомобиль с аккумулятором стоят 110 тыс. руб. Но автомобиль дороже аккумулятора на 100 тыс. Сколько стоит аккумулятор?
https://zen.yandex.ru/media/id/5ee0f3052c7640370e5c0b35/zadal-etu-shkolnuiu-zadachku-prepodavateliu-i-odnogruppnikam-na-lekcii-v-itoge-reshil-tolko-odin-student-5f049373ac46c2398fefe5c5

Почем булочки?
Паша и Алеша решили купить по булочке. Но у них не хватает денег: у Паши рубля, у Алеши девяти рублей.
- А давай, - говорит Паша, - скинемся на одну булочку хотя бы? Съедим пополам.
Алеша соглашается, он скидываются и ... все равно не хватает.
Так сколько же стоила булочка?
[Полуэктов.Озадачник.2017:101-44.]

[192] Полуэктов2017: Полуэктов Павел, Полуэктов Николай: Озадачник: 133 вопроса на знание логики, математики и физики. - М: Альпина Паблишер, 2017. - 286с. Тираж 5000.

Один рабочий может выкопать колодец 1 глубиной 2м и диаметром 1м за 4 часа. В течении скольки часов могут выкопать этот колодец 8 рабочих?
[Коваль.РазвлеченияЗнания.1972:80, задача4].
{А вы попробуйте восьмером копать колодец диаметром 1м}

84. Цена переплета.

Книга в переплете стоит 2.50. Книга на 2 руб. дороже переплета. Сколько стоит переплет?

[193] Перельман2018: Перельман Я.И. 125 лучших задач и головоломок Якова Перельмана. - М: Мартин, 2018. - 192с.

§74.

Сколько времени греется вода?

Запрос в Google по ключевым словам "Время нагрева воды" выдает целую серию сайтов с калькуляторами и советами, как посчитать время нагрева воды, стоимость данного мероприятия, требуемую мощность электронагревателя.

Сколько времени греется вода.
https://nagrev24.ru/voda

Калькулятор времени нагрева воды.
http://serviceelux.ru/instruction/EWH_Boiler_Heating_Calculator.php

{Итог таков: Электронагреватель мощностью 4.2 кВт нагреет 1 л воды на 1 градус за 1 секунду. Электрический чайник такой мощности (чаще все-таки они 1.5 кВт) нагреет 1 литр воды с 20 до 100 градусов за 80 секунд (чуть больше минуты). Соответственно, 1000л (около 1 тонны) он нагреет на 1 градус за 1000с. А на 20 градусов (с 20 до 40) за 20 000с или приблизительно за 6 часов. Теплопотери при этом не учитываются, т.е. реальное время будет больше.}

§75.

[194] Артиллерия1938: Внуков В.П. Артиллерия. - М: Государственное Военное Издательство Наркомата Обороны Союза ССР, 1938. - 360с.
http://wio.ru/galgrnd/artill/art38/vnukov1.htm

[195] Артиллерия1953: Артиллерия. Под ред. полковника Марышева. - М: Военное издательство Народного Комиссариата Обороны, 1953.- 480с.
https://broneboy.ru/книга-артиллерия-1953

Расчет углов и расстояний. Тысячные [Артиллерия1938,с.155-164]:
http://wio.ru/galgrnd/artill/art38/v084.htm

[196] Чуров2016: Чуров В. Загадка «Артиллерии»// Красная Звезда, 11.12.2016.
http://archive.redstar.ru/index.php/advice/item/31568-zagadka-artillerii?attempt=1

§76.

[197] Youtube_AlternativeMath2018: Alternative Math: 2+2=22
https://www.youtube.com/watch?v=Z3IZxHFGFGI

§77.

Савватеев Алексей Владимирович(1973-) - ректор университета Дмитрия Пожарского.

[198] Савватеев2019: Савватеев А.В. Математика для гуммаритариев. Живые лекции. - М: Русский фонд содействия образованию и науке, 2009. - 304с.

"С какой горы на сколько километров видно"
[Савватеев2019p146-150].

Книги, выпущенные издательством Университета Дмитрия Пожарского (Русский фонд содействия образованию и науке), 223 названия [Савватеев2019p287-299].

[199] Савватеев2019: Савватеев А. на собеседовании в Tesla | Гномики, брейнтизеры, головоломки | Математика - просто//Youtube: 29:37.

БРЕЙНТИЗЕРЫ

#305 Вопрос McKinsey: Сколько красных машин в Москве?
[Савватеев2019_00:42]

{П.137. Распределение цветов автомобилей. Красный 5%.}

#306 Вопрос Tesla: Вы стоите где-то на поверхности земли. Пройдя километр на юг, километр на запад и километр на север, вы возвращаетесь на то же место. Где это место?
[Савватеев2019_05:28]
{См. Смаллиан Р. Как же называется эта книга. - М: Издательский дом Мещерякова,2007.
с.17: 14.Задача о медведе. Ответ на с.24}

#307 Вопрос Google: Есть 25 лошадей. Какое минимальное число забегов необходимо провести, чтобы определить 3 самых быстрых лошади? В одном забеге могут участвовать до 5 лошадей, но часов для замера времени у вас нет.
[Савватеев2019_11:07]

#308 Вопрос Amazon: Кабель длиной 80м провисает между двумя столбами высотой 50 м каждый. Чему равно расстояние между столбами, если середина кабеля находится на высоте 20 м над землей? 10 метров над землей?
[Савватеев2019_16:36]

#309 Вопрос из китайской средней школы: Найдите площадь закрашенной фигуры методами школьной математики (без использования интегралов)
[Савватеев2019_21:40]

{Если вышеприведенное изображение открыть в новой вкладке и распечатать, то это будет хорошим началом к попытке решения.}

Обсуждение задачи:
https://pikabu.ru/story/trudnaya_zadacha_7024200

Решение Presh Talwalkar:

[200] Talwalkar2019: Presh Talwalkar: Killer Problem For 11 Year Olds In China//
https://mindyourdecisions.com/blog/2019/10/03/killer-problem-for-11-year-olds-in-china

Решение Valeriy SH (Инженерная Физика):
https://www.youtube.com/watch?v=DLz06IOyhp0

Задача из китайской средней школы. Решение:
https://vipetroff.livejournal.com/7385.html

Еще одно решение:

[201] Савватеев2019: Савватеев на собеседовании в Tesla: Разбор конкурсной задачи //Youtube: https://www.youtube.com/watch?v=mTyT-k2qb-U10:41.

Решение-победитель: Григорий Постников (0:56):

https://pikabu.ru/story/trudnaya_zadacha_7024200

Сам рисунок:
https://cs11.pikabu.ru/images/big_size_comm/2019-11_1/1572765399163311927.jpg

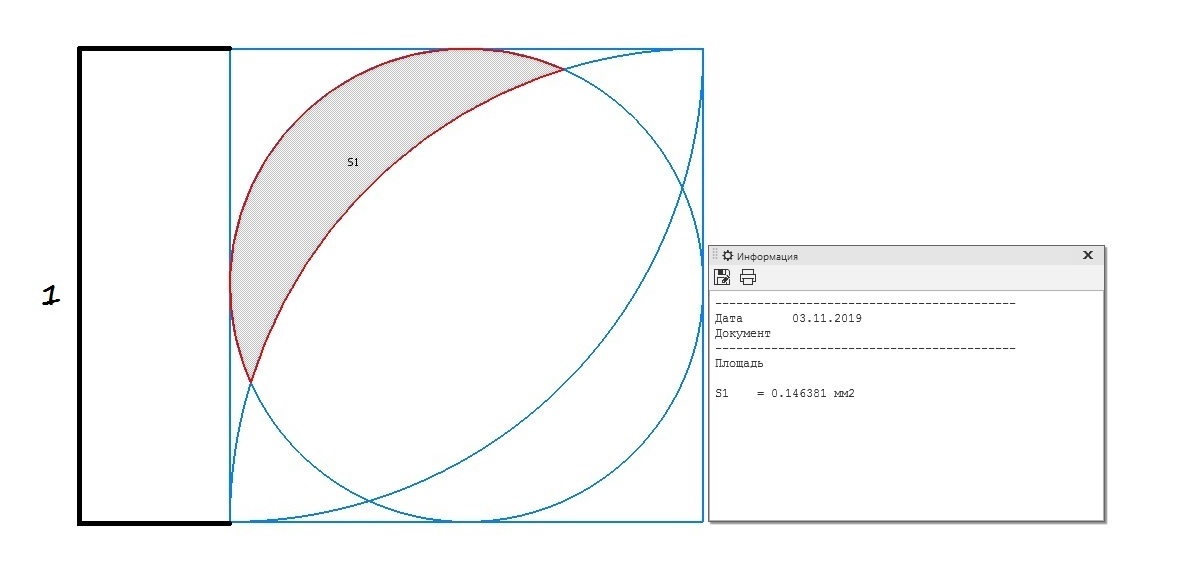
Ответ правильный: 0.146381 кв.мм (При этом сторона малого квадрата равна 1мм и это половина ответа)

Наверное, школьники не пользуются конструкторской программой. Кроме того, решение остается скрытым и виден только ответ, и откуда он взялся - непонятно.

Следующее решение с помощью Excel. Умеют ли китайские школьники в 5-м классе использовать электронные таблицы?
Конечно, вычисление площади под кривой - это численное решение интеграла, но об этом в решении не говорится, а говорится только про суммирование прямоугольников (47 штук), что обеспечивает необходимую точность.

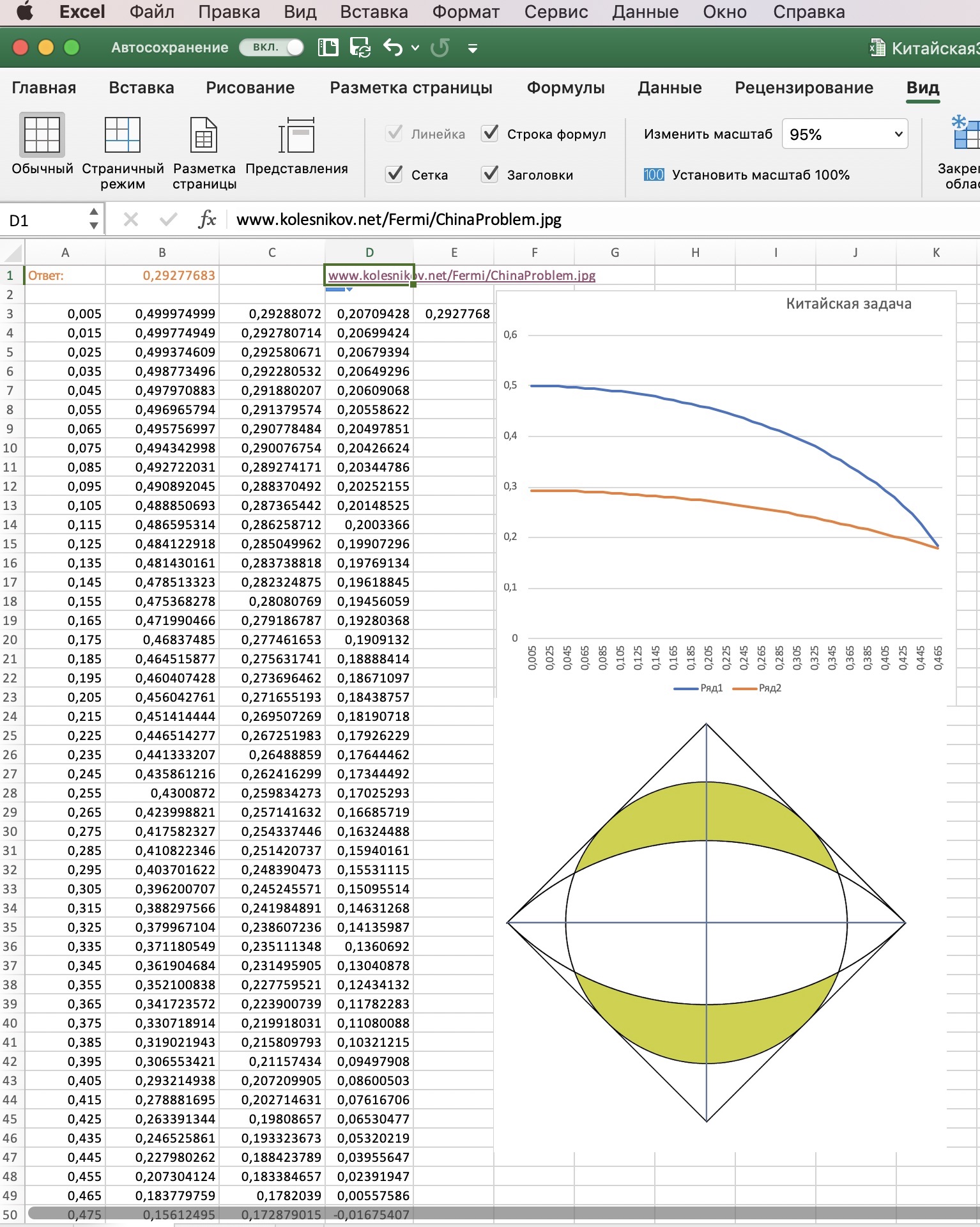
То же решение в качестве таблицы Excel:
https://1drv.ms/x/s!Am-eYGIhJY1LkiDOERpckTBhRweU?e=unayqU

§78.

Стюарт Иэн (Ian Nicholas Stewart)(1945-) The University of Warwick.

[202] Стюарт2019: Стюарт Иэн: Математические диковинки профессора Стюарта. - Пер. с англ. Н.А.Шиховой. - М: Лаборатория знаний, 2019. -320с. Ориг. назв.: Ian Stewart: Professor Stewart’s Cabinet of Mathematical Curiosites. 2009.

[203] Stewart2012: Ian Stewart: In Pursuit of the Unknown. 17 Equations That Changed the World. - NY: Basic Books, 2012. - 342p.

[204] Stewart2016: Ian Stewart: Calculating the Cosmos. How Mathematics Unveils the Universe. - NY: Basic Books, 2016. - 346p.

[205] Stewart2019: Ian Stewart: Do Dice Play God. The Mathematics of Uncertainty. - London: Profile Books, 2019. - 292p.

§79.

[206] Грима2014: Пере Грима. Абсолютная точность и другие иллюзии. Секреты статистики.//Мир математики в 40т. т.13 - Пер. с исп. - М: Де Агостини, 2014. - 144с. - Тираж 200 тыс.

Сайт автора:
http://www-eio.upc.es/~grima/

История холеры. Лондон. 1854. Джон Сноу.
[Грима2014p11-14]

Вспышка холеры на Брод-стрит. 1854г.
https://ru.wikipedia.org/wiki/Вспышка_холеры_на_Брод-стрит
https://en.wikipedia.org/wiki/1854_Broad_Street_cholera_outbreak

[Голдстейн&Голдстейн:Как мы познаем.1984,с.45-81].

[207] Голдстейн_Голдстейн1984: Голдстейн М. Голстейн И. Как мы познаем. Исследование процесса научного познания. - М: Знание, 1984. - 256с.
Ориг. назв.: Martin Goldstein, Inge F.Goldstein: How We Know. An Exploration of the Scientific Process. NY: Da Capo Press, 1978.

Джон Сноу (англ. John Snow)(1813 — 1858),
https://en.wikipedia.org/wiki/John_Snow

Карта района Лондона с признаками холеры, составленная Сноу.
https://en.wikipedia.org/wiki/John_Snow#/media/File:Snow-cholera-map-1.jpg

Найтингейл.1853.[Грима2014p18.]
Флоренс Найтингейл (англ. Florence Nightingale) (1820-1910)
https://ru.wikipedia.org/wiki/Найтингейл,_Флоренс

Закон эпонимов Стиглера. (Stigler's law of eponymy) (Принцип Арнольда).
[Грима2014p63]:

Ни одно открытие не носит имя того, кто в действительности его совершил.

Принцип Арнольда/Lurkmore:
https://lurkmore.to/Принцип_Арнольда

Wikipedia: Закон Стиглера:
https://ru.wikipedia.org/wiki/Закон_Стиглера

Число рыб в озере. Число такси в городе.
[Грима2014p76]

Левши живут меньше (или нет?)
[Грима2014p91]

Опрос по поводу победы Рузвельта.
[Грима2014p93]

David Salsburg: The Lady Tasting Tea
[Грима2014p103]

Fisher R.A.: The Design of Experiment
[Грима2014p103]

Фишер Роналд (англ. Ronald Aylmer Fisher)(1890 — 1962)
https://ru.wikipedia.org/wiki/Фишер,_Роналд

[208] Фишер1958: Фишер Р.А. Статистические методы для исследователей. - М: Госстатиздат, 1958. - 267с.

Аспирин и инфаркты. 1983.
[Грима2014p123-125]

§80.

Как определить возраст дерева.

[209] ru.wikihow.com:
https://ru.wikihow.com/определить-возраст-дерева

[210] Powell2005: David C. Powell (Big-Tree Coordinator Umatilla National Forest) How To Measure a Big Tree. 2005:
https://www.fs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb5202838.pdf

§81.

Кордемский Борис Анастасьевич (1907 — 1999) - автор популярных книг по математике и учебников.
Статьи в журнале Квант: kvant.mccme.ru/au/kordemskij_b.htm

Библиография wiki:

[211] Кордемский1955: Кордемский Б. А. Очерки о математических задачах на смекалку. — М.: Учпедгиз, 1955. — 118 с. — 45 000 экз.

[212] : Кордемский Б. А. Математика изучает случайности. — Просвещение, 1975. — 224 с. — 120 000 экз.

[213] : Кордемский Б. А. Увлечь школьников математикой. — М.: Просвещение, 1981. — 110 с.

[214] Кордемский1995: Кордемский Б. А. Великие жизни в математике. — М.: Просвещение, 1995. — 192 с.

[215] : Кордемский Б. А., Ахадов А. А. Удивительный мир чисел. — М.: Просвещение, 1996. — 159 с. — 2 издания.

[216] : Кордемский Б. А., Островский А. И. Геометрия помогает арифметике. — Физматгиз, 1960. — 128 с. — 125 000 экз. — 2 издания.

[217] Кордемский1963: Кордемский Б. А. Математическая смекалка. — Изд. 7-е, перераб. - М: Физматгиз, 1963. — 576 с. — 150 000 экз.
Новое изд. М: Альпина Паблишер, 2016. - 547с.

[218] Кордемский1952: Кордемский Б. А., Русалев Н. В. Удивительный квадрат. — М.-Л.: ГТТИ, 1952. — 160 с. — 200 000 экз. — 2 издания.

[219] Сканави2017: Егерев В. К., Зайцев В. В., Кордемский Б. А., Маслова Т. Н., Орловская И. Ф., Позойский Р. И., Ряховская Г. С., Сканави М. И. Сборник задач по математике для конкурсных экзаменов во вузы / Под общей редакцией М. И. Сканави. — 5-е изд. - М.: Мир и образование, 2017. — 608 с.

[220] Кордемский2005: Кордемский Б.А. Математические завлекалки. - М: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование», 2005. - 512с. - Тираж 5000.

§82.

Маковецкий Пётр Васильевич (1922—1980) - преподаватель ЛИАП (Ленинградского института авиапроборостроения). Рассматривал вопросы связи с внеземными цивилизациями. Автор "Смотри в корень. Сборник любопытных задач и вопросов" c цитатами из Козьмы Пруткова.

[221] Маковецкий1966: Маковецкий П.В. Смотри в корень! : Сборник любопытных задач и вопросов. - Москва : Наука, 1966. - 232 с. - Библиогр. в конце книги (11 назв.) - Тираж 40 тыс.
2-е изд., перераб. и доп. - Москва : Наука, 1968. - 335 с. - Библиогр.: с. 331-332 (23 назв.) - Тираж 100 тыс.
Также в РГБ и РНБ присутствует второе издание с указанием года: 1969 (Остальные данные те же). Тираж 100 тысяч также.
3-е изд., испр. и доп. - Москва : Наука, 1976. - 447 с. - Тираж 380 тыс.
4-е изд., испр. и доп. - Москва : Наука, 1979. - 382 с. - Тираж 500 тыс.
5-е изд., испр. - М. : Наука, 1984. - 288 с.
6-е изд. - М. : Наука, 1991. - 350,[1] с. ISBN 5-02-014046-5
Два издания на иностранных языках:
Маковецкий П.В. Смотри в корень! : Сб. любопыт. задач и вопр.- Пер. И. Вольф. - М. : Мир, 1985. - 184 с. - Чеш.
Маковецкий П.В. Смотри в корень! : Сб. любопыт. задач и вопр. - Рига : Звайгзне, 1983. - 382 с. - Латыш.
Издание 2013г года:
Маковецкий П.В. Смотри в корень! : сборник любопытных задач и вопросов. - Москва : Книжный Клуб Книговек : Терра, 2013. - 431, [1] с. - 17 см. - (Мир вокруг нас).; ISBN 978-5-4224-0625-8

См. также:
http://publ.lib.ru/ARCHIVES/M/MAKOVECKIY_Petr_Vasil%27evich/_Makoveckiy_P.V..html
Здесь помимо фотографии и краткой биографии можно обнаружить издания "Смотри в корень" 1966, 1968, 1976 и 1979 годов.

§83.

Сингх Саймон (Simon Singh)(1964-) - британский журналист, популяризатор науки, режиссер-документалист.
Авторский сайт: simonsingh.net
Симон Сингх рекомендует математические книги:
simonsingh.net/books/recommended-books/mathematics-books

[222] Сингх2007: Сингх, Саймон (Simon Singh) Книга кодов: тайная история кодов и их взлома. - Пер. с англ. А.Галыгина. - М: АСТ: Астрель, 2007. - 447с.
Ориг. назв.: Simon Singh: The code book. - Fourth Estate Limited, 2000.

[223] Сингх2017: Сингх, Саймон (Simon Singh) Симпсоны и их математические секреты. - 2-е изд. - М: Манн, Иванов и Фербер, 2017. - 272с.
Ориг. назв.: The Simpsons and their mathematical secrets. 2013.

[224] Сингх2000: Сингх, Саймон Великая теорема Ферма. История загадки, которая занимала лучшие умы мира на протяжении 358 лет. - М: МЦНМО, 2000. - 288с.
http://ega-math.narod.ru/Singh/FLT.htm
Ориг. назв. Fermat’s last theorem. The story of a riddle that confounded the world’s greatest minds for 358 years.

§84.

[225] Peck2019: Roxy Peck, Chris Olsen, Tom Short: Introduction to Statistics and Data Analysis. - 6th Edition United States: Cengage Learning, 2018. - 852p.

§85.

Генри Кавендиш (Henry Cavendish)(1731 — 1810)

[226] Cavendish1798: Cavendish H. Experiments to determine the density of the earth // Phil. Trans. of Royal Soc. of London. 1798. Volume 88, р. 469-526.
Опыты по определению плотности Земли
https://archive.org/details/philtrans07861996
На русском языке: Г.Кавендиш Определение плотности Земли//Голин Г.М., Филонович С.Р. Классики физической науки (с древнейших времен до начала XX в.). - М: Высшая школа, 1989. - 576 с., C.253-268.

Генри Кавендиш ставит уникальный эксперимент по «взвешиванию Земли»…
https://vikent.ru/enc/473

Еще говорили, что Кавендиш устроил у себя в доме библиотеку научных книг и открыл в нее доступ всем, кто пожелает ею пользоваться. Каждый посетитель может унести к себе домой любую книгу, оставив хозяину расписку. Шутники утверждали, будто сам Кавендиш так строго и точно соблюдает установленные им в библиотеке порядки, что всякий раз, когда ему случается взять книгу из собственного книжного шкафа, он выдает себе расписку: «Такого-то числа такую-то книгу взял у Генри Кавендиша Генри Кавендиш».

[Бронштейн2013p28]

[227] Бронштейн2013: Бронштейн М.П. Солнечное вещество. Лучи икс. Изобретатели радиотелеграфа. - М: Римис, 2013. - 192с.
По тексту: Бронштейн М.П. Солнечное вещество.- Л: Издательство детской литературы,1936.
https://www.e-reading.club/chapter.php/131109/12/Bronshteiin_-_Solnechnoe_veshchestvo.html

§86.

[228] Голин_Филонович1989: Голин Г.М., Филонович С.Р. Классики физической науки (с древнейших времен до начала XX в.). - М: Высшая школа, 1989. - 576 с.

[229] Капица1976: Капица С.П. Жизнь науки. Антология вступлений к классике естествознания. - М: Наука, 1973. - 600с. Англ. название: The Life of Science. An Anthology of Introduction to Classic in Science. Другое издание: М: Издательский Дом ТОНЧУ, 2008. - 592с.
Содержание

§87.

Задача об астрономических жгутах.

Следующая задача пришла из астрономии. Говорят, что ее задавали на астрономическом конгрессе известным астрономам и никто не дал правильный ответ. Автор услышал данную задачу в Пулковской обсерватории.

Если Землю вытянуть в виде тонкого жгута до Солнца, то какая толщина у этого жгута: тоньше мизинца или толще? А если до ближайшей звезды? А если до Млечного Пути: не будет ли жгут тоньше молекулы?

Задача, на самом деле решается очень легко и это видно, но очевидный ответ не просматривается.

Лобовое и очевидное решение: вычислить объем Земли и посмотреть на объем жгута.

Объем шара 4/3πR³, если принять радиус Земли 6400 км или 6.4*10⁶ м, то получим объем Земли: 1.097*10²¹ м3.

Теперь рассмотрим объем жгута. Для простоты будем считать его сечение квадратным.

Расстояние от Земли до Солнца 150 млн. км или 1.5*10¹¹м.

Если мы разделим объем Земли на длину жгута, то получим площадь его сечения:

7.3*10⁹ м²,

из которой путем извлечения корня можно определить толщину жгута (жгут же квадратный):

8.5*10⁴ м или 85 км, что очевидно, толще мизинца.

Если считать жгут с круглым сечением, то его R = √S/π = 4.8 10⁴ м, а его толщина равна удвоенному радиусу или 96 км.

Таким образом, приводимый ответ в 100 км является корректным.

Однако задача имеет более простое оценочное решение:

Посмотрим на Землю как на куб с гранью 12 тыс. км., это приблизительно в 10000 раз меньше расстояния до Солнца (с ошибкой в 25% - =:)). Две другие грани уменьшим в 100 раз и получим толщину жгута в 120 км, что, очевидно, несколько больше толщины мизинца. Вычисления очень просты, а ответ не сильно отличается от точного для такой сильно гипотетической задачи.

Рассмотрим вопрос замены шара кубом с гранью в два радиуса шара. Условно, шар можно положить в этот куб. Определим коэффициент объемной коррекции.

Объем шара 4/3πR³, объем куба (2R)³ = 8R³.

a = 4/3πR³ = 8R³

a = 1.91,

т. е. при замене шара кубом размером грани в диаметр, объем увеличивается почти в два раза. Это надо учитывать, когда вы заполняете какое-либо помещение тенисными мячами. (Отметим, что есть более эффективные способы размещения шаров в ограниченном пространстве).

Теперь растянем Землю до ближайшей звезды. Это альфа Центавра, 4 световых года.

Скорость света, как известно из многочисленных опытов, составляет грубо 300 тыс. км/с.

(3*10⁸ м/с)

В сутках 60*60*24 = 86 400 секунд.

В году 365 дней и 31 536 000 секунд.

Четыре года содержат 126 144 000 секунд. (1.2*10⁸c)

Несмотря на то, что на 4 года с высокой степенью вероятности, придется один високосный год, по моему мнению, этим в данном расчете можно пренебречь.

Таким образом, длина жгута составит 3.6*10¹⁶ м, что в 2.4*10⁵ (240 000) раз больше расстояния от Земли до Солнца. Соответственно, сечение нашего жгута меньше в 240 000 раз, а каждая сторона при квадратном сечении меньше в 500 раз. (Если точно 489 раз). Если в жгуте до Солнца это было 85 км, то теперь жгут вытянулся до 170 м.

Продолжим вытягиваение жгута: теперь цель - Млечный путь. Центр нашей Галактики находится в направлении Созвездия Стрельца. До него 27 700 световых лет.

Это расстояние больше расстояния до Альфа Центавра в 6925 раз. Толщина нашего жгута уменьшится в 83 раза и составит 2 метра, что опять-таки толще мизинца.

Таким образом, мы видим, что расчеты гипотетического вытягивания реальных предметов на космические расстояния, показывают вполне обозримый размер жгута.

Разновидностью данной задачи можно считать задачу Парселла [Purcell1984, Miscellaneous-1(A long wire)], где предлагается из железа земной коры сделать провод и пронянуть его на радиус видимой части вселенной (10²⁸ см). Расчеты показывают, что диаметр провода будет порядка 1 мм.

Вывод из этой задачи следующий: даже простая задача с очевидным решением (как вычислить толщину жгута через объем) далеко не так очевидна навскидку и, как показала практика, даже профессионалы с ходу не дают правильного решения.

Задача 62. Сообщена Перельману Я.И. проф. А.В. Цингером.
[Перельман1923:74-75]
Цингер Александр Васильевич(1870-1934)
https://ru.wikipedia.org/wiki/Цингер,_Александр_Васильевич

[230] Перельман1923 Перельман Я. И. Практические занятия по геометрии. Образцы, темы и материалы для упражнений. - М-Петроград: Государственное издательство, 1923. - 176с.
http://publ.lib.ru/ARCHIVES/P/PEREL'MAN_Yakov_Isidorovich/_Perel'man_Ya.I..html#0042

§88.

Дамодаран Асват (Aswath Damodaran) (1957-) New York University Stern School of Business.
https://en.wikipedia.org/wiki/Aswath_Damodaran Личный сайт:
http://pages.stern.nyu.edu/~adamodar/

[231] Дамодаран2012: Дамодаран Асват: Оценка стоимости активов. - Пер. с англ. П.А.Самсонов. - Минск: Попурри, 2012. - 272с.
Ориг. назв.: Aswath Damodaran: The Little Book of Valudation (How to Value a Company, Pick a Stock, and Profit). 2011.

[232] Дамодаран2018: Дамодаран Асват: Инвестиционная оценка. Инструменты и методы оценки любых активов. - 11-е изд. - М: Альпина Паблишер, 2018. - 1316с.
Aswath Damodaran: Investment Valuation: Tools and Techniques for Determining the Value of any Asset.

§89.

Задача о трех стрелках, иначе именуемая "труэль".

[Вербер2010p168-169]

[233] Вербер2010: Бернар Вебер: Энциклопедия относительного и абсолютного знания. - М: Geleos Publishing House: РИПОЛ классик, 2010. - 288с.

[Мостеллер1971:12, 20. Трехсторонняя дуэль]

§90.

[234] Kolecki2000: Joe Kolecki: NASA: Mathematical Thinking in Physics
https://www.grc.nasa.gov/WWW/k-12/Numbers/Math/Mathematical_Thinking/index.htm

Заметки о математическом мышлении в физике на сайте NASA.

Копия в Web.Archive:
http://web.archive.org/web/20180825021051/ https://www.grc.nasa.gov/WWW/K-12/Numbers/Math/Mathematical_Thinking/index.htm

§91.

Метод Монте-Карло (Улам_Метрополис1949)

[235] Metropolis_Ulam1949: N. Metropolis; S. Ulam: The Monte Carlo Method// Journal of the American Statistical Association, Vol. 44, No. 247. (Sep., 1949), pp. 335-341.
https://www.chemie1.unibas.ch/~meuwly/download/ulam.mc.pdf

Stable URL: https://www.jstor.org/stable/2280232

[236] Тепляков2001: Тепляков Андрей: Моделируя жизнь //Hard'n'Soft. N 7. 2001.
http://arbuz.uz/z_pihns.html

§92.

[237] Riverbend.2017: Riverbend Community Math Center: План урока по задачам Ферми:
https://www.mathcircles.org/wp-content/uploads/2017/10/Fermi_Estimates_Lesson_Plan_0-1.pdf

§93.

[238] Maxwell.2009: Daniel Maxwell: How many grams of gas has been burned by all of the cars in the world ever since the invention of the automobile?

https://web.archive.org/web/20101111033443/ http:/www.google.com/base/a/1551686/D2256477437979091778

{Сколько грамм топлива было сожжено всеми автомобилями с момента их изобретения.
Годового потребления (больше 1 куб.км, но меньше 2-х) хватит, чтобы растопить процентов 25% триллионника}

§94.

Триллионник.

10-12 июня 2017г. от Антарктиды откололся айсберг А-68 площадью 6000 кв. км и массой около 1 триллиона тонн (10¹²). Число производит впечатление. Хотя, учитывая плотность льда, легко вычислить толщину айсберга (где-то 170м). Между прочим, поражающую воображение массу скорее всего вычислили именно зная толщину льда и площадь айсберга.

[239] Про айсберг написало BBC:
http://www.bbc.com/news/science-environment-40321674

И указало место, где находится айсберг:

[240] Статья в Wikipedia про А-68:
https://ru.wikipedia.org/wiki/Айсберг_А-68

[241] Снимки NASA:
https://earthobservatory.nasa.gov/images/91052/a-68-adrift

Снимок 16 сентября 2017 года.

Плавление льда.

Для того, чтобы расплавить 1 кг льда требуется энергия в 372 кДж = 3.72*10⁵ Дж. Одна килотонна равна 4.18*10¹² Дж. Отсюда можно получить, что 1 кт хватит на растопление 10⁷ кг =10 кт льда.

Если вернуться к триллионнику, то мощность самой мощной царь-бомбы составит около 50 мегатонн, что позволит растопить 500 млн. тонн льда или 0.05% триллионника. Немного однако.

Оцените массу льда, которую можно расплавить, имея ведро кипятка.
[§98, Бондаров.ОценочныеЗадачи.2016:421,Задача 2.]
Ответ: 13 кг.

§95.

[242] Tyson1994: Neil de Grasse Tyson: Universe Down to Earth. - New York: Columbia University Press, 1994. - 277p.
{Вселенная спустилась на Землю}

Wikipedia:
https://ru.wikipedia.org/wiki/Тайсон,_Нил_Деграсс
https://en.wikipedia.org/wiki/Neil_deGrasse_Tyson

Adam.Guesses.1995,p.20 отмечает, что хорошо относятся к задачам Ферми:
Глава 1. A Sentimental Journey to the Googleplex- Сентиментальное путешествие в Гуглеплекс.
[Tyson1994p3-12]
Глава 3. Measure for Pleasure - Измерения для удовольствия.
[Tyson1994p37-45]

§96.

[243] Кусов2009: Кусов В.С. (1935-2009) Измерение Земли: История геодезических инструментов. - М: Дизайн. Информация. Картография, 2009. - 256с. - Тираж 1000 экз.

https://ru.wikipedia.org/wiki/Кусов,_Владимир_Святославович

§97.

[244] Крылов_Бутенко1995: Крылов А.С., Бутенко А.В. Задачи которые может решить каждый. Книга для очкариков... и не только. / Краснояр. гос. ун-т; Сост. А.С. Крылов, А.В. Бутенко. Красноярск, 1995, 148с.
http://kirensky.ru/zdoc/KLSh_book.pdf

§98.

Бондаров Михаил Николаевич. Учитель физики. Лицей 1501. г.Москва.
https://lycc1501.mskobr.ru/common_edu/ osnovnoe_i_srednee_obwee_obrazovanie_quot_1501_quot/ obwie_svedeniya/pedagogicheskij_kollektiv/fizika/bondarov_mihail_nikolaevich

Персональный сайт.
http://physics.lyceum1501.ru

Публикации
http://xn--80aaehfbdnibse7ai3audo8byp.xn--p1ai/publikacii.html

[245] Бондаров2016: Бондаров М.Н. Роль оценочных задач в преподавании физики // Сборник научно-практических материалов по итогам IV Московских методических чтений «Фестиваль методических идей». – М.: 2016. С. 417 – 422.
http://xn--80aaehfbdnibse7ai3audo8byp.xn--p1ai/publikacii/sbornik_n-p-mater_mn.pdf

Три примера:
1. Энрико Ферми. Вопросы. (Оцените число настройщиков роялей в Чикаго)
2. Гранин: Иду на грозу. Сколько тысяч жителей разбудил мотоцикл?
3. Иосиф Шкловский: Сколько людей в тюрьмах?

Реальность числовых значений в задачах:
Индукция магнитного поля в 20 Тл
Тепловой двигатель с КПД 75%.

#310 Оценка количества книг, которые человек прочитал за всю жизнь.
[Бондаров2016p419]

#311 Пример 1. Сколько человек может поместиться в телефонной будке.
[Бондаров2016p420]

Рекорд на 1984г. - 24 человека.

#312 Пример 2. Сент-Экзюпери: Разместить все человечество на острове в Тихом океане. Оцените размер острова.
[Бондаров2016p420]

Камин А.Л. Физика. Развивающее обучение. Книга для учителей. 7-й класс. – Ростов н/Д: Изд-во «Феникс», 2003. (можно найти в эл. виде)

#313 Пример 3. Молекула из последнего дыхания Цезаря.
[Бондаров2016p420]

Коган Б.Ю. Число Авогадро и предсмертный вздох Юлия Цезаря. // Квант. – 1973. – № 9.

#314 Пример 4. С какой скоростью плывут заморские гости на картине Рериха.
[Бондаров2016p420]

Стасенко А.Л. Волны на воде и «Заморские гости» Н. Рериха. // Квант. – 1972. – № 9.

#315 Пример 5А: Оцените, какое количество пар обуви использует женщина в течение жизни.
[Бондаров2016p421]

#316 Задача 1. Оцените, как быстро пройдет мимо Вас современный поезд.
[Бондаров2016p421]
Решение. Ответ: 14с

#317 Задача 2. Оцените массу льда, которую можно расплавить, имея ведро кипятка.
[Бондаров2016p421]
Решение. Ответ: 13 кг.

#318 Задача 3. Оцените, какое количество лампочек надо включить в квартире, чтобы выбило пробки.
[Бондаров2016p421]
Решение.

#319 Задача 4. Оцените минимальную скорость, которую необходимо сообщить маленькому шарику, чтобы он перелетел из одного конца классной комнаты в другой.
[Бондаров2016p422]

Максимальная дальность полета (при угле вылета 45^о ) в 4 раза больше максимальной высоты подъема.

#320 Задача 5. Оцените максимальную высоту прыжка в крытом спортивном зале на Луне.
[Бондаров2016p422]

Маковецкий П.В. Смотри в корень! – М.: Наука. Гл. ред. физ.-мат. лит., 1991. { с.38: Задача 16. Прыгуны на Луне.}

§99.

[246] Камин2003: Камин А.Л. Физика. Развивающее обучение. Книга для учителей. 7 класс. - Ростов н/Д: Изд-во "Феникс", 2003. - 352с.
http://www.vixri.com/d/ Kamin%20A.L.%20%20_Fizika.%207kl.%20Razvivajushee%20obuchenie.pdf

§100.

[247] Коган1973: Коган Б. Число Авогадро и предсмертный вздох Юлия Цезаря//Квант. 1973. N 9. С.71,73.
http://kvant.mccme.ru/1973/09/chislo_avogadro_i_predsmertnyj.htm

Число Авогадро: 6^.10²³. (Количество атомов или молекул в 1 моле вещества. 1 моль газа в нормальных условиях - 22 литра.)

Авогадро Амедео (Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e Cerreto)(1776-1856) - итальянский химик.
https://ru.wikipedia.org/wiki/Авогадро,_Амедео

Джеймс Хопвуд Джинс  (James Hopwood Jeans) (1877-1946) — британский физик-теоретик, астроном, математик.
https://ru.wikipedia.org/wiki/Джинс,_Джеймс_Хопвуд

[248] Jeans1940: Sir James Jeans: An Introduction to the Kinetic Theory of Gases. Cambridge: Cambridge University Press, 1940. - 320p.

[Jeans1940p32.]
books.google.ru

Последнее дыхание Цезаря:
[Baeyer1993p116]

§101.

[249] Объем кита1982: Как определить объем кита, плавающего у берегов Гренландии.// Квант, 1982. N 9.
http://kvant.mccme.ru/1982/09/kak_opredelit_obem_kita_plavay.htm

Статья из серии "Квант улыбается". Ни одного реального способа измерить кита не предложено.

§102.

[250] Стасенко1972: Стасенко А. Волны на воде и "Заморские гости" Н. Рериха//Квант. 1972. N9. с.10-15.
http://kvant.mccme.ru/1972/09/volny_na_vode_i_zamorskie_gost.htm

#321 С какой скоростью плывут заморские гости?
Определяется с помощью носовых и круговых волн. Причем носовые волны выдают скорость 2.25-2.7 м/с, а круговые волны - только 0.7 м/с. Отметим, что 2.25 м/с составляет около 8 км/ч, что определяется с помощью умножения на 3600 и перевода полученной величины в километры путем деления на 1000.

Заморские гости. 1901.Холст, масло. 85x112,5 см. Государственная Третьяковская галерея, Москва.
https://ru.wikipedia.org/wiki/Рерих,_Николай_Константинович

§103.

[251] Левитин2019: Дэниел Левитин. Организованный ум. Как мыслить и принимать решения в эпоху информационной перегрузки. - М: Манн, Иванов и Фербер, 2019. - 544с.
Ориг.назв.: Daniel J. Levitin: The Organized Mind. Thinking Straight in the Age of Information Overload.

Задача Ферми о настройщиках пианино в Чикаго.
[Левитин2019p416-419]

#322 Сколько весит Эмпайр-стейт-билдинг?
[Левитин2019p415-423]

#323 Положительный анализ.
[Левитин2019p276-284p446-456.]

§104.

[252] Тэтлок2018: Тетлок Филип, Гарднер Дэн: Думай медленно - предсказывай точно. Искусство и наука предвидеть опасность. - М: Издательство АСТ, 2018. - 384с.
Ориг. назв.: Philip Tetlock, Dan Gardner: SUPERFORECASTING: The art and Science of Prediction. 2015.

Метод Ферми [Тэтлок2018p139-143].

§105.

[253] Posamentier:The Mathematics of Everyday Life.2018: Alfred S. Posamentier, Christian Spreitzer: The Mathematics of Everyday Life. - New York: Prometeus Books, 2018. - 424p.

Упоминается продажа Манхэттена местными индейцами голандскому губернатору Петеру Мануиту (Peter Minuit) в 1626 году в контексте инвестирования этих средств на несколько сотен лет. (Задача Баффета). [Posamentier:The Mathematics of Everyday Life.2018,p.100]

Правило 72. [Posamentier2018p104]

Задача Монти Холла. Что выбрать: козла или машину? [Posamentier2018p154]

Самая лучшая крышка люка. [Posamentier2018p117]

[254] Позаментье_Крулик2018: Позаментье Альфред, Крулик Стивен: Стратегия решения математических задач. - Пер. с англ. В.Ионова. - М: Альпина Паблишер, 2018. - 223с. - Тираж 1500.
Ориг. назв.: Alfred S. Posamentier, Stephen Krulik: Problem-Solving Strategies in Mathematics from Common Approaches to Elementary Strategies.

У нас 100 кг свежих ягод, в которых 99% массы приходится на воду. Через некоторое время содержание воды в ягодах снижается до 98%. Сколько теперь весят ягоды?
[Позаментье_Крулик2018p29]

Глава 2. Распознавание закономерности.
[Позаментье_Крулик2018p41]

Задача 3.2. В распоряжении Лорен 11-литровый и 5-литровый сосуды. Как ей отмерить точно 7 литров воды?
[Позаментье_Крулик2018p65]

§106.

[255] Куприн1976: Куприн А.М. Топография для всех.- М: Недра, 1976. - 168с.

Измерения на расстоянии
[Куприн2018p15-19]

§107.

[256] Горобец2002: Горобец Б. Ошибочная точность// Наука и жизнь. 2002. N3.
https://www.nkj.ru/archive/articles/3970

§108.

Взгляни на мир с другой стороны.

[257] Сорокина2019: Сорокина О. Мир один, а "Карты мира", оказывается, очень разные! Почему так?// Мир открытыми глазами: Яндекс Дзен.
https://zen.yandex.ru/media/olga_sorokina/mir-odin-a-karty-mira-okazyvaetsia-ochen-raznye-pochemu-tak-5dde5ebd8294e33d61cd128c

§109.

[258] Fless2020: Fless: Виктор Рогуленко: Форт Боярд Математиков | Wild Mathing, Савватеев, Трушин, Побединский, Зубков, Павликов.

Тексты задач:
https://fless.pro/форт-боярд-математиков

Задача 1. Чемодан

#324 Вы плывете в лодке и выбрасываете за борт чемодан. Поднимется или опустится уровень воды?
[Fless2020]

На мой взгляд, наиболее понятное решение Бориса Трошина:
https://www.youtube.com/watch?v=f2VLdwU9xc4&t=62s

Чемодан вместе с лодкой вытесняет V = (M + m)/ρ, где
M - масса лодки,
m - масса чемодана,
ρ- плотность воды.
Дальше чемодан выбросили и если он плавает, то
V = M/ρ + m/ρ и объем вытесненной воды не изменится.
Если чемодан наполнен золотом, то он утонет:
m делится уже на плотность золота (19.32 г/см³), объем вытесненной жидости уменьшится (поскольку лодка облегченно всплывет), уровень воды понизится.
Третий, экзотический, случай отмечен Савватеевым: если чемодан улетит, будучи легким и наполненным гелием, лодка тяжело осядет и уровень воды повысится.

{Интересно оценить эффект понижения уровня воды в случае чемодана, наполненного золотом:
Рассмотрим бассейн нового русского размером 20 на 5 метров и глубиной 2 метра. В нем находится 200 кубических метров воды.
Пусть объем чемодана - 40 литров. Если его наполнить золотом, то он будет весить: 19.3*40 = 772 кг.
Допустим, поднатужившись и используя рычаг, вы выкинули его за борт.
Лодка облегченно поднялась. Объем вытесенной жидкости уменьшился на 772 литра. Но сам чемодан увеличил объем на 40 литров. Итого: 732 литра.
Площадь поверхности бассейна: 100 кв. метров. Объем уменьшился на 0.732 куб. метра, а уровень примерно на 7.5 мм.
Далее, можно заметить, что изменение уровня воды пропорционально площади бассейна. Эффект от чемодана на площади от 1000 кв.метров практически не будет заметен.
Для справки: грубая оценка стоимости 772 кг золота составляет около 35 млн. долларов США:
1 тройская унция на бирже стоит примерно 1.5 тыс. долларов, в кг примерно 30 тройских унций (32.15), килограммов всего 772
Другие варианты наполнения чемодана:
Платина: ρ = 21.45 г/см³
Уран: ρ = 19.1 г/см³
Вольфрам: ρ = 19.26 г/см³
Иридий: ρ = 21.56 г/см³
Осмий: ρ = 22.59 г/см³}

Задача 2. Шары и взвешивания

#325 Имеется 8 шаров одинакового размера. 7 из них весят поровну, а один – чуть тяжелее. За какое минимальное количество взвешиваний можно гарантированно найти тяжелый шар, используя только чашечные весы без гирь?
[Fless:ФортБоярдМатематиков.2020]

{Ответ: 2 раза. Сначала взвешиваем 3 и 3, а два шара откладываем. Если на весах равенство, то взвешиваем два отложенных. Один из них должен быть тяжелее. Если одня чаша весов в первом случае тяжелее, то берем из тяжелой троицы 2 любых шара и взвешиваем. Весы укажут на более тяжелый шар. Если не укажут, то более тяжелый отложенный шар.
Это решение хорошо математически, но в реальной жизни поведет себя плохо, если неизвестно, легче или тяжелее один из шаров и, вообще, если он не один.}

Задача 3. Озеро

#326 Вы находитесь в лодке точно в центре абсолютно круглого озера. На берегу озера Злой Дух. Дух замышляет против вас что-то недоброе, но он не умеет плавать и даже летать, и лодки у него тоже нет. Если вы сумеете причалить к берегу, а Дух не сумеет вас там подкараулить и сразу же схватить, вы всегда сумеете на земле от него убежать и вырваться на свободу. Дух может бежать со скоростью в 4 раза выше, чем скорость вашей лодки. У него безупречное зрение, он никогда не спит и мыслит очень рационально. Он сделает все возможное, чтобы поймать вас. Как бы вы могли убежать от Злого Духа?
[Fless2020]

Задача 4. Зелёные бумажки

#327 Представьте, что вас пятерых схватил Злой Дух, посадил в разные комнаты и прикрепил на лоб бумажки. Каждое утро вы собираетесь в Тайной комнате и видите друг друга, однако общаться друг с другом не можете, а также не имеете возможности увидеть себя. Дух сообщает, что каждый из вас может прийти к нему ночью и попроситься на свободу. Если бумажка у вас на лбу зеленая, то Дух отпустит вас, если нет – убьет. Дух – еще тот хитрец и любитель математиков, и потому все бумажки популяризаторов зеленые, однако ни один из вас об этом на знает. Дух рассказал всем вам, что есть хотя бы один популяризатор с зеленой бумажкой. Как вам действовать, чтобы всем гарантированно выбраться на свободу?
[Fless2020]

Задача 5. Шкафчики

#328 В одной из школ есть такой ритуал, проводящийся в последний день занятий: ученики выходят в холл и стоят около своих шкафчиков, в которых хранится одежда. По 1-ому свистку каждый ученик открывает свой шкафчик. По 2-ому свистку ученики закрывают четные шкафчики (то есть шкафчики с номерами 2, 4, 6 и т.д.) По 3-ему свистку ученики меняют положение дверцы каждого 3-его шкафчика, то есть если она была открыта, её закрывают, а если закрыта – открывают. Это происходит со шкафчиками с номерами 3, 6, 9 и т.д. По 4-ому свистку меняется состояние дверцы каждого 4-го шкафчика, по 5-ому свистку каждого 5-ого и т.д. Предположим для простоты, что это небольшая школа и шкафчиков всего 100. По сотому свистку ученик, который стоит рядом со шкафчиком под сотым номером (и только этот ученик), меняет положение дверцы этого шкафчика. Сколько шкафчиков после этого оказываются открытыми?
[Fless2020]

Задача 6. Дух и математики

#329 Злой Дух поймал двух популяризаторов науки, Дмитрия Побединского и Алексея Савватеева, и посадил их в разные комнаты своего страшного дома. Затем Злой Дух подбросил симметричную монетку бесконечное количество раз. Все результаты чётных бросков он сообщил Дмитрию, а все результаты нечётных – Алексею. Далее Дух предлагает каждому популяризатору назвать номер любого подбрасывания, результат которого ему не известен. То есть Дмитрий должен назвать нечётный номер, а Алексей – чётный. Если результаты бросков, названных Дмитрием и Алексеем, одинаковые, то Злой Дух дарит каждому популяризатору свободу. Если же результаты бросков отличаются, то Злой Дух съедает популяризаторов в надежде поумнеть. Алексей и Дмитрий, конечно, знают о повадках Злого Духа и могли заранее до похищения договориться о стратегиях. Какую стратегию им выбрать, чтобы вероятность спасения была больше 50%?
[Fless2020]

{В комментариях к [Fless2020] пользователь koleso1v указал ответ: надо называть номер первого орла. Как это не пародоксально, вероятность того, что ответы совпадут 2/3. }

Два способа решения приведены на канале Бориса Трушина (второй из них аналогичен вышеприведенному):

[259] Трушин2020: Борис Трушин: Задача про монетку из шоу "Форт Боярд Математиков"/Ботай со мной #070
https://www.youtube.com/watch?v=oAj4xPXKzwg

Блиц 1.1. Гендерное равенство

#330 В некоторой стране семьи рожают детей до тех пор, пока не родится девочка. Мальчики и девочки рождаются с вероятностью 50-50. Какова доля мальчиков в такой стране?
[Fless:ФортБоярдМатематиков.2020]

{Задача разбирается в [Паундстоун2013p249-250],
[Гамов2003p20-23].}

Блиц 1.2. Математический алфавит

#331 У вас есть 26 констант, обозначенных буквами от А до Z. Пусть А равняется 1. Значение следующей константы будет определяться рекурсивно: порядковым номером данной буквы в английском алфавите, возведенном в степень, соответствующую значению предыдущей константы. Это значит, что значение В (вторая буква) равно 2 в степени А, то есть 2 в степени 1 = 2. С равно 3 в степени B, то есть 3 в квадрате = 9 и т.д. Найдите точное численное значение выражения: (Х-А) х (Х-В) х (Х-С) х … х (X-Z)
[Fless2020]

Блиц 1.3. Баночка с драже

#332 У вас баночка, в которой драже 3 цветов: красного, зеленого и синего. Вам нужно с закрытыми глазами взять из баночки только 2 драже так, чтобы они оказались одного цвета. Сколько драже вам нужно достать, чтобы быть уверенным, что среди них есть 2 одинакового цвета?
[Fless2020]

Блиц 2.1. Шнур Форта Боярд

#333 У вас есть два куска бикфордова шнура. Каждый из них горит в течение ровно 1 часа, но куски могут быть неидентичными и необязательно горят с постоянной скоростью: есть фрагменты, которые горят быстро, а есть такие, которые горят медленно. Каким образом можно узнать, что прошло 45 минут, используя только эти куски бикфордова шнура и зажигалку?
[Fless2020]

Блиц 2.2. Стрелки встречаются

#334 Сколько раз в день пересекаются минутная и часовая стрелки механических часов?
[Fless2020]

Блиц 2.3. Два яйца

#335 Дано 100-этажное здание. Если яйцо сбросить с высоты N-го этажа (или с большей высоты), оно разобьется. Если его бросить с любого меньшего этажа, оно не разобьется. У вас есть 2 яйца. Найдите N за минимальное количество бросков.
[Fless2020]

[260] Трушин2020: Борис Трушин: Разбор задач шоу "Форт Боярд Математиков"/Ботай со мной #069/feat. Wild Mathing.

[261] Зубков2020: Владимир Зубков: Форт Боярд Математиков - РЕШЕНИЕ.

§110.

[262] Побединский2020: Побединский Дмитрий: Чердак. Только физика, только хардкор. - М: Издательство АСТ, 2019. - 320с.

Детектор лжи [Побединский2020p266]

§111.

Как определить высоту объекта вблизи или на расстоянии? Основные 5 способов!
https://zen.yandex.ru/media/building_for_myself/ kak-opredelit-vysotu-obekta-vblizi-ili-na-rasstoianii-osnovnye-5-sposobov-5db00a1e7cccba00adeaf130

§112.

[263] МТ-75: Мореходные таблицы 1975г. (МТ-75). - Л: Главное управление навигации и океанографии Министерста обороны СССР, 1975. - 324с. - Предыдущее издание: МТ-63.
http://deckofficer.ru/titul/study/item/mt-75

Таблица 22 в МТ-75 (Мореходные таблицы 1975 года,с.248), позволяет рассчитать географическую дальность видимости предмета путем двукратного входа в нее по е и по h, а затем сложения результатов.
Отметим, что 1 морская миля равна 1852м
http://www.glubinnaya.info/science/ geograficheskaya-dalnost-vidimosti-predmetov-dalnost-vidimogo-gorizonta-6389.html

Номограмма Струйского.
https://ru.wikipedia.org/wiki/Струйский,_Николай_Николаевич

Оценочная формула для линии горизонта L (в км):

L = 3.6(√h+√e),

где h - высота предмета в метрах,
e - высота глаза наблюдателя в метрах.

Если расстояние измерять в морских милях (1852м), то коэффициент при корнях 2.08. Если все считать в метрах (что более корректно, но менее удобно), то коэффициент 3600.

Если смотреть с самолета с высоты 10 тыс.м, то линия горизонта будет в 360 км. Теоретически, пролетая Бологое, можно одновременно видеть Москву и Петербург [Савватеев2019p149].

[264] Перельман1934: Перельман Я.И. Как далеко видно со стратостата?//Техника — молодежи. 1934. №2. с. 70-71.
http://epizodyspace.ru/bibl/tehnika_-_molodyoji/1934/1/70-71.djvu

§113.

Тьюки Джон John Wilder Tukey (1915-2000) Автор терминов software и bit, соавтор алгоритма Кули-Тьюки (Быстрого преобразования Фурье).
https://ru.wikipedia.org/wiki/Тьюки,_Джон

[265] Тьюки1981: Тьюки Дж. Анализ результатов наблюдений. Разведочный анализ. - М: Мир, 1981. - 693с. - Тираж 15 тыс.
Ориг. назв.: John W. Tukey: Explorary Data Analysis.

Краткий конспект на 16 страницах:
http://baguzin.ru/wp/wp-content/uploads/2016/11/Джон-Тьюки.-Анализ-результатов-наблюдений.-Разведочный-анализ.pdf

[266] Конник2014: Конник Михаил (Virens): История создания алгоритма Быстрого Преобразования Фурье (БПФ)//Пост в блоге. 2014. (Библиогр. 13 назв.)
http://mydebianblog.blogspot.com/2014/07/blog-post.html

§114.

[267] Горстко1970: Горстко А.Б. В поисках правильного решения. (О принципах рациональный деятельности человека). - М: Знание, 1970. - 78с.

§115.

Определение скорости света по спутникам Юпитера. Метод Ремера. 1676.

Олаф Кристенсен Рёмер (дат. Ole Christensen Rømer)(1644—1710)
https://ru.wikipedia.org/wiki/Рёмер,_Оле

Измерение скорости света Ремером:
https://ru.wikipedia.org/wiki/Измерение_скорости_света_Рёмером

[268] Römer1676: "Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Académie Royale des Sciences"// Journal des Sçavans du Lundy 7 Decembre 1676. p. 233–36, (in French):
https://cral-perso.univ-lyon1.fr/labo/fc/ama09/pages_jdsc/pages/jdsc_1676_lumiere.pdf
Перевод статьи Ремера 1676г. приведен в
[Голин_Филонович1989p117-120].

...Необходимо 22 минуты для прохождения удвоенного расстояния от нас до Солнца. [Голин_Филонович1989p120]

{Это расстояние, как известно нам (но не Ремеру), равно 150 млн. км. Поделив на калькуляторе:
2*150 млн.км/(22*60c)= 227 тыс. км/с.
Мы-то знаем, что скорость света 300 км/с. Поэтому погрешность у Ремера 24%.
Кстати, если бы Ремер считал, например, что до Солнца 190 млн. км, то скорость света была бы посчитана точнее =:)}

[269] Gibbs1997: Philip Gibbs: How is the speed of light measured?
http://www.ronen.net/physics/Relativity/SpeedOfLight/measure_c.html
Русский перевод:
Как измерили скорость света
http://cyber-ek.ru/science/measure_c.html

[270] Филонович1983: Филонович С.Р. Самая большая скорость. - М: Наука, 1983. - 176с.

Новое измерение скорости света//Квант. N1. 1973. с.50
http://kvant.mccme.ru/1973/01/novoe_izmerenie_skorosti_sveta.htm

§116.

[271] Себрант2016: Себрант А.Ю. (1954-) Почему машинное обучение меняет бизнес и жизнь? Выступление Андрея Себранта, Директора по маркетингу сервисов компании ЯНДЕКС на конференции Трансформация.ORG 19 октября 2016.
https://ru.wikipedia.org/wiki/Себрант,_Андрей_Юлианович
Личный сайт: http://www.sebrant.ru

https://www.youtube.com/watch?v=hibuaty2O7U

Информационные технологии стали операционными.

Коты на газоне.  NVIDIA engineer Robert Bond.

[272] Caulfield2016: Brian Caulfield: How One NVIDIAN Uses Deep Learning to Keep Cats from Pooping on His Lawn July 7, 2016.
https://blogs.nvidia.com/blog/2016/07/07/deep-learning-cats-lawn
Русский перевод: Как отучить соседского кота гадить на газон: используем машинное зрение и глубокое обучение.
https://habr.com/ru/post/395821

О Роберте Бонде:
https://devblogs.nvidia.com/author/rbond

[273] Bond2016: Robert Bond: Build an AI Cat Chaser with Jetson TX1 and Caffe. August 2, 2016.
  https://devblogs.nvidia.com/ai-cat-chaser-jetson-tx1-caffe

Сортировка огурцов. Как японский фермер при помощи глубокого обучения и TensorFlow огурцы сортировал.
https://habr.com/ru/post/397305

TensorFlow powered cucumber sorter by Makoto Koike
https://www.youtube.com/watch?v=4HCE1P-m1l8

How a Japanese cucumber farmer is using deep learning and TensorFlow:
https://cloud.google.com/blog/products/gcp/how-a-japanese-cucumber-farmer-is-using-deep-learning-and-tensorflow

§117.

Сколько минут вы потеряете, если максимальная разрешенная скорость будет снижена на 5 км (или миль, например)?
[Slavin1999p126 Speed Limit Problems].

[274] Slavin1999: Steve Slavin: All the Math You’ll Ever Need. A Self-Teaching Guide. Revised Edition. - New York: John Wiley & Sons, Inc., 1999. - 230p.

§118.

Богданов-Бельский Н. П. (1868—1945)
Устный счёт. В народной школе С. А. Рачинского(1833—1902). 1895
Холст, масло. 107,4 × 79 см
Государственная Третьяковская галерея, Москва
https://ru.wikipedia.org/wiki/Устный_счёт._В_народной_школе_С._А._Рачинского

(10²+11²+12²+13²+14²)/365 = ?

В Википедии приводятся пара методов решения с помощью разложения квадратов, но по мне проще всего сосчитать в лоб: 100+121+144+169+196, а потом заметить, что сумма первых трех чисел равна 365, как и сумма двух оставшихся. Ответ 2. Даже калькулятор в общем-то не нужен.

Более продвинутые методы в статье:

[275] Транковский2006: Транковский С. Устный счет//Наука и жизнь. N7. 2006.
http://www.nkj.ru/archive/articles/6347

[276] Рачинский2014: 1001 задача для умственного счета в школе С.А.Рачинского. М.: Белый город, воскресный день, 2014. -144с. Формат чуть-меньше А4.

Решение задачи Рачинского (4 способа):
https://4brain.ru/blog/решение-задачи-рачинского

[277] Фаермарк1974: Фаермарк Д.С. Задача пришла с картины. М.: Издательство "Наука", 1974. - 160с. - Библиогр. с.159 (34 назв.) {О С.А.Рачинском}

[278] Полознев2005: Полознев Г. Сбывшееся предсказание//Наука и жизнь. N12.2005:
http://www.nkj.ru/archive/articles/3008

Что больше 34 или 42. {Калькулятор в данном случае не поможет.}
...устный счет не просто полезный бытовой навык. Это одно из средств оценки и прогнозирования обстановки, инструмент самостоятельного мышления.
[Полознев:Сбывшееся предсказание.2005]

§119.

Монета встает на ребро

Утро. Общага. Звонит будильник. Просыпаются студенты 1-5 курса.
Первокурсник: Ребят, может учиться пойдем?
Второкурсник: Не, лучше доспим.
Третьекурсник: А может пивка выпить?
Четверокурсник: А может водочки?
Пятикурсник: Ребят, давайте монетку кинем. Если орлом упадет, то пивка выпьем, если решка - то водочки. Если ребром упадет - доспим, ну а если в воздухе зависнет, тогда учиться пойдем...
Старый анекдот
https://pikabu.ru/story/staryiy_anekdot_1695175

#336 Какой толщины должна быть монета, чтобы вероятность выпадения "на ребро" составляла 1/3?
[Секей1990p68]

[279] Епифанов2016:
elementy.ru: Епифанов Е. Толстая монета. 2016:
https://elementy.ru/problems/1449/Tolstaya_moneta

[Секей1990p68]

[280] Секей1990: Секей Габор. Парадоксы в теории вероятностей и математической статистике. - Переводчик В. Ульянов. - М: Мир, 1990. - 240с.
Ориг. назв.: Gabor J. Szekely: Paradoxes in Probability Theory and Mathematical Statistics. 1986.

[281] Yong_Mahadevan2011: Ee Hou Yong, L.Mahadevan: Probability, geometry, and dynamics in the toss of a thick coin// Am. J. Phys. 79 (12), December 2011. p.1195-1201.
https://www.seas.harvard.edu/softmat/downloads/2011-13.pdf

[Мостеллер1975p17_Условие_p71-72_Решение]

Мостеллер Фредерик (Frederick Mosteller)(1916–2006)
https://en.wikipedia.org/wiki/Frederick_Mosteller

[282] Мостеллер1975: Мостеллер Ф.: Пятьдесят занимательных вероятностных задач с решениями. - М: Наука, 1975. - 112с. Тираж 250 тыс.

{А кто сказал, что монета круглая? Квадратные тоже встречаются. Тогда она может превратиться в кубик и на боковые грани будет выпадать в 4 раза чаще, чем на орел и решку.
Дальше было бы неплохо рассмотреть вариант, когда монета падает сверху на ребро. Обычная монета при падении на ровную нелипкую поверхность упадет набок. Какой толщины она должна быть, чтобы падать набок с вероятностью 2/3 (по 1/3 на каждый бок), а с вероятностью 1/3 оставаться на ребре?}

§120.

Гаусс Карл Фридрих (англ. Johann Carl Friedrich Gauss) (нем. Johann Carl Friedrich Gauß)(1777-1855)
https://ru.wikipedia.org/wiki/Гаусс,_Карл_Фридрих

«Теперь я расскажу историю о маленьком Гауссе, будущем знаменитом математике. Она заключается в следующем: шестилетним мальчиком он учился в средней школе небольшого городка. Учитель предложил контрольное задание по арифметике объявил классу: “Кто из вас первым найдет сумму 1+2+3+4+5+6+7+8+9+10? Очень скоро, в то время как остальные все еще были заняты вычислениями, юный Гаусс поднял руку. “Liggetse”- сказал он, что означало “Вот!”. “Каким образом, черт побери, тебе это так быстро удалось”- воскликнул пораженный учитель. Юный Гаусс ответил – конечно, мы не знаем точно, что он ответил, но на основании экспериментального опыта я считаю, что он ответил приблизительно так: “Если бы я искал сумму, складывая 1 и 2, затем, прибавляя к сумме 3, затем к новому результату – 4 и т.д., то это бы заняло очень много времени; и,  пытаясь сделать это быстро, я, пожалуй, наделал бы ошибок. Но, посмотрите, 1 и 10 в сумме дают 11, 2 и 9 снова в сумме  составляют 11. И так далее! Существует 5 таких пар; 5 умноженное на 11 даст 55”.
[Вертгеймер1987p142]

[283] Вертгеймер1987: Вертгеймер М. Продуктивное мышление. М: Прогресс, 1987. - 336с.

Эта же история в изложении Познера В.

Когда мне было лет семь, я спросил у своего папы: «А что такое гений?». И вот он рассказал мне историю: в XVII веке был мальчик, ему было шесть лет, фамилия его была Гаусс. И вот он пошел в школу. А в классе было человек сорок. Учителю очень скучно – учить детей считать – умножать, делить и так далее. Тем более что учителю попалась хорошая книжка, он хотел почитать. И он думал – как же мне их занять? И он сказал: значит, так, дети – я хочу, чтобы вы сложили все цифры от единицы до ста: один, два, три, четыре, пять и так далее. Думайте. Он полагал, что это их займет надолго. И сел читать. Но буквально через две минуты он видит, что один мальчик тянет руку (это был Гаусс). – Что, тебе в туалет? – Нет, у меня есть ответ. – Как это? Какой у тебя ответ? – Пять тысяч пятьдесят. Учитель и сам не знал ответ, просто хотел их занять. Говорит – а как это у тебя получилось? Тот: господин учитель, это очень просто: представьте все цифры от единицы до ста – не столбиком, а в ряд. Представили? Видите две крайние цифры – один и сто. И сложите – сколько будет? – Сто один. Следующие две: два и 99, сколько будет? – Сто один. – Три и 98. Сколько будет? – Сто один. И мы доходим до 50 и 51– опять 101. Значит, 50 раз по 101, это пять тысяч пятьдесят. И учитель понял, что он имеет дело с гением.

Владимир Познер: «Я осознал, что беру интервью у гения» - Познер Online
https://pozneronline.ru/2019/01/23894

Подобную задачу рассматривает [Mahajan2014p69-70]
Sanjoy Mahajan(1969-): The art of insight in science and engineering. Mastering complexity. - Cambridge, Massachusetts: MIT Press, 2014. - 390 p. - Библиогр. p.359-361 (50 назв.)

Еще есть формула для суммы ряда: S = 1/2*(a1+an)*n

Как быстро найти сумму ряда на Excel: посчитать ряд в несколько тысяч членов не составит ни труда, ни времени. Вжик .. и все.

Гильде.МикрокалькуляторВРуках.1987:21. По стопам юного Гаусса:

§121.

Сколько будет: 6/2(1+2)=?

{После 2 перед скобкой пропущен знак умножения. Если его поставить, то будет 6/2*3=. Если руководствоваться правилами приоритета, (сначала в скобках, потом умножение/деление, далее сложение/вычитание), то результат равен 9. Однако, у многих, если не у большинства, возникает мысль, что 2 без знака умножения привязана к скобкам (в том числе имеются и подтверждения этой мысли из классических источников). Поэтому лучший ответ сформулирован в ГОСТ Р 54521-2011 Знак умножения может быть опущен, если ошибка исключена. Поскольку в данному случае ошибка не исключена, а даже наоборот, то формулировка задачи записана некорректно и имеет два ответа. Более того, ответ 6/2(1+2)=1 имеет значительно большую вероятность.
Некоторые математики считают, что задача не из области математики, а из области филологии. Но мне кажется, что хоть задача и из области филологии, но относится все равно к математике, и никуда математикам от этого не деться.
Кратко говоря, надо ставить скобки в нужных местах и не пропускать знаки умножения, а если вы этого не сделали и вас не поняли, то не надо говорить про приоритет знаков и "на зеркало пенять".
ГОСТ в контексте данного вопроса упомянут в [Трушин2019], а ссылка на ГОСТ и выписка из него приводится ниже. Кстати употребление звездочки * (как в языках программирования FORTRAN, C, Pyton) в качестве знака умножения противоречит данному ГОСТу. }

6/2(1+2): Excel предлагает исправить ошибку на ‭=6/2*(1+2)‬ и получить 9.

6/2(1+2): Python выдает ошибку и ничего не предлагает.

[284] Трушин2019: Трушин Борис: Одиозный дед и Hitman. 6:2(1+2)=1//В интернете опять кто-то неправ #003:
https://www.youtube.com/watch?v=ypSF_bRbFbY&feature=emb_rel_end

[285] Talwalkar2016: Presh Talwalkar: What Is 6÷2(1+2) = ? The Correct Answer Explained:
https://mindyourdecisions.com/blog/2016/08/31/what-is-6%c3%b7212-the-correct-answer-explained

[286] Haelle2013: Tara Haelle: What Is the Answer to That Stupid Math Problem on Facebook? And why are people so riled up about it?//slate.com, MARCH 12,2013:
https://slate.com/technology/2013/03/facebook-math-problem-why-pemdas-doesnt-always-give-a-clear-answer.html

[287] ГОСТ Р 54521-2011: ГОСТ Р 54521-2011. Статистические методы. Математические символы и знаки для применения в стандартах
http://docs.cntd.ru/document/gost-r-54521-2011

Знак умножения может быть опущен, если ошибка исключена:

[288] Thequestion.ru2016: Чему равно 6÷2(1+2)?//Thequestion.ru, январь 2016:
В ответах ссылки на Ландау,Лившиц; Вольфрам Альфа.
https://thequestion.ru/questions/71351/chemu_ravno_6_2_1_2_bafc737c

[289] Теории и практики2019: Как решать вирусные математические задачи//Теории и практики,21 августа 2019
https://theoryandpractice.ru/posts/17626-kak-reshat-virusnye-matematicheskie-zadachi

[290] Lamb2019: Evelyn Lamb: The Only Way to Win Is Not to Play the Game What to do with those pesky order of operations questions?//blogs.scientificamerican.com, August 3, 2019
https://blogs.scientificamerican.com/roots-of-unity/the-only-way-to-win-is-not-to-play-the-game

[291] Strogatz2019: Steven Strogatz: The Math Equation That Tried to Stump the Internet.//www.nytimes.com, Aug. 2, 2019.
https://www.nytimes.com/2019/08/02/science/math-equation-pedmas-bemdas-bedmas.html

[292] Miles2019: Frank Miles: Viral math problem baffles mathematicians, physicists// Fox News, August 1, 2019
https://nypost.com/2019/08/01/viral-math-problem-baffles-mathematicians-physicists

{Колмогоров. Идея о приоритете умножения. Не принята.}

§122.

#337 Математик Теодор Хилл давал задание студентам записать результаты 200 бросков монеты. А некоторым - придумать эти результаты. И практически безошибочно определял придуманные результаты. Сложно придумать группу из шести орлов или решек подряд, которая обычно есть в реальных результатах.
[Паундстоун2015p58]

Теодор Хилл (Theodore Hill) (1943-) Georgia Institute of Technology (Atlanta, Georgia)
https://en.wikipedia.org/wiki/Ted_Hill_(mathematician)

Real & Fake coin flips [Gelman_Nolan2002p105]

[293] Gelman_Nolan2002: Andrew Gelman, Deborah Nolan: Teaching Statistics: A Bag of Tricks. Oxford: Oxford University Press, 2002. - 316p.

[294] Kouritzin2002: Michael A. Kouritzin, Fraser Newton, Sterling Orsten and Daniel C. Wilson: On Detecting Fake Coin Flip Sequences//IMS Collections: Markov Processes and Related Topics: A Festschrift for Thomas G. Kurtz Vol. 4 (2008) 107–122
https://projecteuclid.org/download/pdfview_1/euclid.imsc/1233152938

[295] Browne1998: Malcolm W. Browne: Following Benford's Law, or Looking Out for No. 1// The New York Times, Tuesday, August 4, 1998
http://www.rexswain.com/benford.html

[296] МатематическаяУгроза2018: Роман Тайный: Гендерный скандал: как феминистки обиделись на теорему//www.forbes.ru, 11.09.2018 11:09:
https://www.forbes.ru/tehnologii/366615-gendernyy-skandal-kak-feministki-obidelis-na-teoremu

Комментарий к методу Теодора Хилла с помощью программной модели:
05.05.2020 Tuesday 11:00 Метод Теодора Хилла: Подбрасываем монету 200 раз. Находим максимальное число единиц. И так 10000 раз.
Максимальное количество единиц подряд в серии из 200 подбрасываний:
[0, 0, 0, 4, 360, 1747, 2634, 2093, 1449, 838, 440, 222, 101, 58, 30, 14, 6, 1, 1, 1, 0, 1, 0, 0, 0]
В четырех опытах максимум 4 единицы подряд (1111), в 360 - пять единиц (111111). В остальных - шесть (111111) и более.
Метод не работает в 364/10000=3.64% случаев.

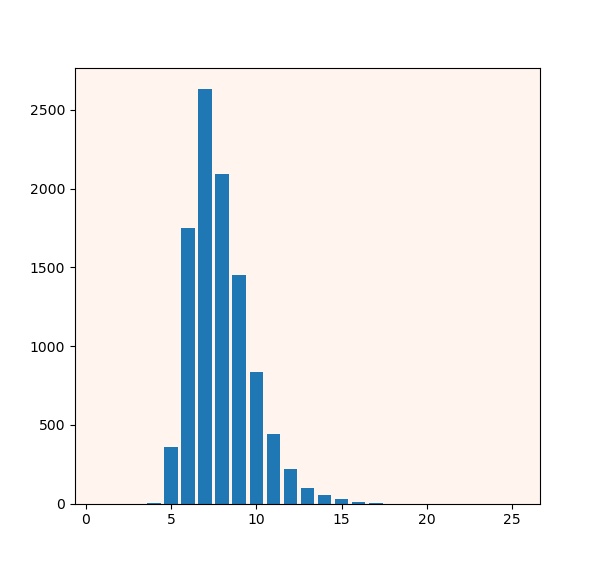
Число опытов с максимальным числом единиц подряд.

§123.

Стивен Левитт (Steven D. Levitt)(1967-) Чикагский университет.
https://ru.wikipedia.org/wiki/Левитт,_Стивен

[297] Левитт_Дабнер2011: Левитт С., Дабнер С. Фрикономика. - М.: Манн, Иванов и Фарбер, 2011. - 272 с.

[298] Левитт_Дабнер2010: Левитт С., Дабнер С. Суперфрикономика. - М.: Манн, Иванов и Фарбер, 2010. - 288 с.

[299] Левитт_Дабнер2015: Левитт С., Дабнер С. Фрикомыслие: нестандартные подходы к решению проблем. - М.: Альпина паблишер, 2015. - 199 с. (подписано в печать 16.10.2014)
Ориг. назв.: Steven D. Levitt, Stephen J. Dubner: Think like a freak. The authors of Freakonomics offer to retrain your brain.

[300] Левитт_Дабнер2016: Левитт С., Дабнер С. Когда грабить банк и другие лайфхаки.- Пер. с англ. - М.: Альпина Паблишер, 2016. - 240 с.
Steven Levitt, Stephen Dubner: When to Rob a Bank... and 131 more warped suggestions and well-intended rants. 2015.

[301] Ельяшевич2010: Ельяшевич А.М. (1937-) Метод выявления скрытых закономерностей – Data Mining и/или фрикономика?// Выступление в Междисциплинарном лектории Контекст 18 февраля 2010 года.
http://www.contextfound.org/events/y2010/m2/n40

Ельяшевич А.М. (1937-)
http://www.contextfound.org/speakers/alexey-yeliashevich

[302] Тарушкин2013: Тарушкин А.Б. Антифрикономика. - СПб.: Сотис-Мед, 2013. - 152с.

Влияние отмены запрета абортов на криминал (Статья в Wikipedia):
https://en.wikipedia.org/wiki/Legalized_abortion_and_crime_effect

[303] DonohueIII_Levitt2001: John J. DonohueIII, Steven D. Levitt: The Impact of Legalized Abortion on Crime// The Quarterly Journal of Economics. Vol. CXVI. May 2001. Issue 2.
http://pricetheory.uchicago.edu/levitt/Papers/ DonohueLevittTheImpactOfLegalized2001.pdf

§124.

[304] Указ:О системе российских мер и весов1835: Указ Императора Николая I от 11 октября 1835 года «О системе российских мер и весов» // Полное собрание законов Российской Империи. Собрание Второе. Том X. Отделение 2. 1835 г. - СПб: Тип. II Отделения Собственной Его Императорского Величества Канцелярии, 1836. - 910с. (с.1010-1011).
https://www.runivers.ru/bookreader/book9878/#page/93/mode/1up

§125.

Четыркин Евгений Михайлович (1926-)
https://ru.wikipedia.org/wiki/Четыркин,_Евгений_Михайлович

[305] Четыркин2000: Четыркин Е.М. Финансовая математика: Учеб. - М: Дело, 2000. - 400с. (BiblioCloud)

Манхэттен, Индейцы 6.3% годовых
[Четыркин2000p45].

Компенсация в Бхопале (Индия)
[Четыркин2000p109-110].

Рента принцессы Дианы
[Четыркин2000p114].

§126.

1811 года дядя мой Василий Львович, по благорасположению своему ко мне и ко всей семье моей, во время путешествии из Москвы в Санкт-Петербург, взял у меня взаймы 100 рублей ассигнациями, данных мне на орехи покойной бабушкой моей Варварой Васильевной Чичериной и покойной тетушкой Анной Львовною. Свидетелем оного займа был известный Игнатий; но и сам Василий Львович, по благородству сердца своего, от оного не откажется. Так как оному прошло уже более 10 лет без всякого с моей стороны взыскания или предъявления, и как я потерял уже всё законное право на взыскание вышеупомянутых 100 рублей (с процентами за 14 лет, что составляет более 200 рублей), то униженно молю его высокоблагородие, милостивого государя дядю моего, заплатить мне сии 200 рублей по долгу христианскому — получить же оные деньги уполномочиваю князя Петра Андреевича Вяземского, известного литератора.
Коллежский секретарь Александр Сергеев сын Пушкин.
15 августа 1825.
Село Михайловское.
https://sheba.spb.ru/bib/slonimsky-pushkin.htm

"Какой процент годовых разумел Пушкин, подсчитывая сумму дядюшкиного долга?"
Сложный процент: 100*(1+0.01p)**14=200; p=5.2%
Простой процент: (200-100)/14 = 7.1%. Все расчеты приблизительны.
[Карпушина2013p48-49p53]

[306] Карпушина2013: Карпушина Н.М. Вне формата. Занимательная математика: гимнастика для ума или искусство удивлять? - М: АНО Редакция журнала "Наука и жизнь", 2013. - 288с. - Тираж 2000.

[307] Гессен1930: Гессен Сергей: Книгоиздатель Александр Пушкин. Литературные доходы Пушкина. - Л: Академия, 1930. - 148с.
Перепечатка с изд. 1930г.: М: Захаров, 2008. - 128с.

Клиентка сообщила Шерлоку Холмсу, что в наследство от дяди ей досталось 2500 фунтов стерлингов. Деньги хранились в банке и приносили доход в размере 4.5% годовых. Женщина снимала проценты с вклада ежеквартально. Какую сумму она получала?

[Карпушина2017p24,131]

{Берем 4.5% от капитала (112.5 фунтов). Делим его на четыре (28.125). Выясняем, что в 1 фунте 20 шиллингов, в 1 шиллинге 12 пенсов во времена Шерлока Холмса.
28 фунтов 2 шиллинга 6 пенсов.
Остается выяснить, какая сумма соответствует этому в современных реалиях:
Курс фунта к доллару в 1880г. 5.0.
12 500 долларов 1880г. эквивалентны где-то 300-600 тыс. долларов 2015 года.
http://kolesnikov.net/Currency.html }

[308] Карпушина2017: Карпушина Н.М. Любимые книги глазами математика. Занимательные задачи и познавательные истории для взрослых и детей. - 2-е изд., испр. и доп.. - М: АНО Редакция журнала "Наука и жизнь", 2017. -168с - Тираж 2000.

§127.

Расчет налога на депозиты 13%

Итак, предложение, которое может затронуть многих, — обложить НДФЛ процентные доходы по вкладам, общий объем которых превышает миллион рублей. Президент отдельно подчеркнул: не сам депозит, а только проценты, получаемые от таких вложений. Что это означает на практике? Например, у вас есть вклад в размере 1,1 млн рублей под ставку 6% годовых. Налог будет исчисляться только с суммы дохода — 66 тыс. рублей, НДФЛ составит примерно 8,6 тыс. Как подчеркнул Владимир Путин, эта мера затронет порядка одного процента вкладчиков. Как показывает статистика, объем средств населения на депозитах перевалил за 30 трлн рублей. При этом, по данным Агентства по страхованию вкладов, в среднем граждане хранят в банках (без счетов до тысячи рублей) около 180 тыс. рублей. На вклады до миллиона от общего объема депозитных средств приходится около 37%, от миллиона и выше — порядка 55%. Проще говоря, самый высокий процент сбережений в банках имеет меньшинство.

На основании статистики в НРА рассчитали, что при средней обещанной доходности в 6% налогооблагаемая база в годовом выражении составит примерно 0,98 трлн рублей, что при ставке НДФЛ в 13% принесет в бюджет около 130 млрд рублей.

— Еще порядка 20 млрд рублей налоговых поступлений могут поступить за счет инвестиционных счетов населения свыше миллиона рублей. Следовательно, от анонсированной президентом меры бюджет получит около 150 млрд рублей в год, — уточнил директор рейтингов финансовых институтов НРА Юрий Ногин.

Каледина А., Гринкевич Д.: В пользу бедных: зачем России налог на доходы с крупных банковских вкладов. По оценкам экспертов, предложенная президентом мера принесет бюджету порядка 150 млрд рублей.// Известия, iz.ru. 26 марта 2020, 00:01
https://iz.ru/991544/anna-kaledina-dmitrii-grinkevich/v-polzu-bednykh-zachem-rossii-nalog-na-dokhody-s-krupnykh-bankovskikh-vkladov

По данным Агентства по страхованию вкладов (АСВ), на 1 марта 2020 года в России было открыто 594 млн счетов (в том числе вкладов) физлиц и индивидуальных предпринимателей. Статистика не учитывает общую сумму средств в разных банках, которые держит один клиент, то есть вкладчик, имеющий счета в двух банках, учитывается дважды, пояснили РБК в АСВ. Общий объем средств на счетах - 31,47 трлн руб. На вклады от 1 млн руб. приходится порядка 57% от этой суммы (17,95 трлн руб.), но количество таких счетов - 1% (5,9 млн единиц).

Чернышова Е., Кошкина Ю.: Банки пожаловались в ЦБ на заявления клиентов о закрытии вкладов. Они увидели первые признаки «набега» вкладчиков// www.rbc.ru, Финансы , 27 мар, 00:00
https://www.rbc.ru/finances/27/03/2020/5e7ce4369a794723cb66f2db

Обращение Президента Путина В.В. из-за ситуации с коронавирусом//youtube.com, 25.03.2020
https://www.youtube.com/watch?v=KY8kMSXQIsM

Обращение Президента Путина В.В. к россиянам. Главное.25.03.2020
https://www.m24.ru/articles/vlast/25032020/156557

§128.

Немецкая танковая задача.

Немецкие танки нумеровались следующим образом: 1,2,3... N, где N — требуемое общее количество выпущенных танков. Допустим, войсками захвачено пять танков с серийными номерами 20, 31, 43, 78 и 92. Итак, выборка состоит из пяти танков, максимальный серийный номер 92. Назовем размер выборки S, а максимальный серийный номер — M. После нескольких экспериментов с другими сериями статистики пришли к выводу, что вероятная оценка количества танков описывается простым уравнением (М-1)(S+1)/S. В нашем примере это приводит к (92-1) (5+1)/5, что равно 109,2. Соответственно производство танков в этот период составляло 109. Используя эту формулу, статистики оценили производство танков в Германии за период с июня 1940 по сентябрь 1942 в 245 единиц в месяц, в то время как разведка Британии оценивала ежемесячное производство танков в Германии в 1 400 единиц. Разница в пять раз. После войны из захваченных документов стало известно, что немцы производили в течение этих трех лет по 246 танков в месяц. Сейчас подобное извлечение данных стало обыденностью и поставлено на поток.

[309] Борисов2013: Борисов А. Деревянная бомба, или история феномена «больших данных» от фараонов до Второй мировой. 9 августа 2013.
http://www.computerra.ru/81037/history-bigdata

Немецкая танковая задача на англ:
https://en.wikipedia.org/wiki/German_tank_problem
На немецком:
https://de.wikipedia.org/wiki/German_tank_problem

[310] Goodman1952: Leo A. Goodman: Serial Number Analysis// Journal of the American Statistical Association Vol. 47, No. 260 (Dec., 1952), pp. 622-634.
Published by: Taylor & Francis, Ltd. on behalf of the American Statistical Association
DOI: 10.2307/2280780
https://www.jstor.org/stable/2280780

[311] Goodman:Some Practical Techniques.1954: Leo A. Goodman: Some Practical Techniques in Serial Number Analysis// Journal of the American Statistical Association Vol. 49, No. 265 (Mar., 1954), pp. 97-112
Published by: Taylor & Francis, Ltd. on behalf of the American Statistical Association
DOI: 10.2307/2281038
https://www.jstor.org/stable/2281038

Leo Goodman (1928-)
https://en.wikipedia.org/wiki/Leo_Goodman

[312] Davies2006: How a statistical formula won the war//Gavyn Davies does the maths. www.theguardian.com. 19 Jul 2006.
https://www.theguardian.com/world/2006/jul/20/secondworldwar.tvandradio

[313] Ruggles_Brodie1947: Richard Ruggles and Henry Brodie: An Empirical Approach to Economic Intelligence in World War II// Journal of the American Statistical Association Vol. 42, No. 237 (Mar., 1947), pp. 72-91
Платно: https://www.jstor.org/stable/2280189
Бесплатно на сайте ЦРУ:
https://www.cia.gov/library/readingroom/document/cia-rdp79r01001a001300010013-3

[314] Volz2008: Arthur G. Volz: A Soviet Estimate of German Tank Production// The Journal of Slavic Military Studies Volume 21, 2008 - Issue 3. Pages 588-590. Published online: 29 Aug 2008.
https://doi.org/10.1080/13518040802313902

[Scheaffer1996p148].

[315] Scheaffer1996: Richard L. Scheaffer, Jeffrey Witmer, Ann Watkins, Mrudulla Gnanadesikan Activity-Based Statistics: Student Guide. - New York: Springer Verlag, 1996. - 251p.
books.google.ru

В середине ХХ века последователь Байеса математик Гарольд Джеффрис пытался определить количество трамваев в городе, имея в качестве вводной информации серийный номер только одного трамвая, и ответ его был таким же: надо просто умножить серийный номер на два. Еще одна похожая задача появилась раньше, во время Второй мировой войны, когда страны Антанты хотели подсчитать количество танков, производимых Германией. Чисто математические подсчеты на основании серийных номеров захваченных танков показали, что немцы производили 246 танков в месяц, в то время как, по оценкам обширной (и крайне опасной) воздушной разведки, количество ежемесячно производимых за этот период танков составляло примерно 1400 единиц. После окончания войны немецкие архивы раскрыли истинную цифру: 245 танков в месяц.

[Кристиан_Гриффитс2017p197]
{Кажется, имеется в виду не серийный номер трамвая и их количество, а номер маршрута и количество маршрутов.}

[Robert2009p17] 5.3 The Tramcar Problem.

[316] Robert:Jeffreys’s Theory.2009: Christian P. Robert, Nicolas Chopin and Judith Rousseau: Harold Jeffreys’s Theory of Probability Revisited// Statistical Science 2009, Vol. 24, No. 2, 141–172
DOI: 10.1214/09-STS284
https://arxiv.org/pdf/0804.3173.pdf

[317] Steil2011: Michael Steil: How many Commodore 64 computers were really sold? 2011-02-01.
https://www.pagetable.com/?p=547

(а). На железной дороге N поездов с номерами 1,2,...,N. Однажды вам встретился поезд с номером 60. Угадайте, сколько поездов на железной дороге.
(б). Вы повстречали 5 поездов, причем 60 по-прежнему наибольший номер. Снова постарайтесь угадать, сколько всего поездов на железной дороге.
[Мостеллер.ПятьдесятЗадач1971_18,41_Задача о поездах]

[318] Мостеллер1971: Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. - М: Наука, 1971. - 104с.
Ориг. назв.: Frederick Mosteller: Fifty Challenging Problems in Probability: With Solutions. 1988. - 88 p.

[319] Johnson1994: Roger W. Johnson: Estimating the Size of a Population, June 1994.
https://doi.org/10.1111/j.1467-9639.1994.tb00688.x

http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid =9C5A97497E6C537E98ED12DC34C76646?doi=10.1.1.385.5463&rep=rep1&type=pdf

§129.

13.2.3. Методы оценки размеров популяции (Глава 13. Количественная экология)

[320] Грин1990: Грин Н., Стаут У., Тейлор Д. Биология. В 3-х т. - М: Мир, 1990. - 1069с.
http://biologylib.ru/books/item/f00/s00/z0000018/st134.shtml

[321] Коросов2007: Коросов А. В. Специальные методы биометрии. Петрозаводск, 2007. 364 с.

Коросов А.В.
https://petrsu.ru/persons/870/korosov
Публикации А.В. Коросова (В т.ч. раздел Биометрия)
http://korosov.narod.ru

§130.

Статистическая оценка человеческой жизни.

[322] Viscusi_Aldy2003: W. Kip Viscusi, Joseph E. Aldy: The Value of a Statistical Life: A Critical Review of Market Estimates Throughout the World//The Journal of Risk and Uncertainty, 27:1; 5–76, 2003.
http://camra.msu.edu/documents/ViscusiandAldy2003.pdf

[323] Решетова2013: Екатерина Решетова: Жизнь – не бесценна. Высокая цена человеческой жизни, закрепленная документально, стимулирует мероприятия по сокращению смертности и повышению безопасности на дорогах.// Национальный исследовательский университет «Высшая школа экономики»: Научно-образовательный портал IQ.
https://iq.hse.ru/news/177670487.html

[324] Гуриев2020: Сергей Гуриев: ВВП или жизни людей. Пожертвовавший жизнями ради экономического роста не получит ни того, ни другого//Ведомости/Мнения/Аналитика, 26 марта, 21:37
https://www.vedomosti.ru/opinion/articles/2020/03/27/826385-vvp-lyudei

§131.

COVID-19

[325] Pueyo2020: Tomas Pueyo: Coronavirus: Why You Must Act Now Politicians, Community Leaders and Business Leaders: What Should You Do and When?//medium.com, 10 Mar 2020.
https://medium.com/@tomaspueyo/coronavirus-act-today-or-people-will-die-f4d3d9cd99ca
На русском языке: Коронавирус: почему надо действовать прямо сейчас.
https://habr.com/ru/post/491974

[326] Пестов2020: Пестов Илья: Коронавирус: как мы себя обманываем.//18 марта 2020 в 18:40.
https://habr.com/ru/post/492946

{Критика вышеприведенной статьи на основании того, что оценка 1% смертности основана на крайне малых данных.}

Глава рабочей группы по COVID-19 Алексей Боровков : Пик эпидемии будет 25 мая, но только если петербуржцы будут сидеть дома.
https://https://www.fontanka.ru/2020/04/29/69232996

[327] Ижуткин_Сёмин2020: Ижуткин В.С., Сёмин П.Н.Программная реализация математических моделей распространения эпидемий.// Международный журнал экспериментального образования. – 2015. – № 2-1. – С. 32-33:
https://www.expeducation.ru/ru/article/view?id=6403
(дата обращения: 03.05.2020)

Kermack–McKendrick theory
https://en.wikipedia.org/wiki/Kermack%E2%80%93McKendrick_theory

Compartmental models in epidemiology.
https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology

[328] Kermack_McKendrick1927: Kermack W. O. and McKendrick A. G. A Contribution to the Mathematical Theory of Epidemics // Proc. Roy. Soc. Lond. — 1927. — A 115, pp. 700–721.

Модель Кермака и Маккендрика.

William Ogilvy Kermack (1898 – 1970)
https://en.wikipedia.org/wiki/William_Ogilvy_Kermack

Anderson Gray McKendrick(1876 – 1943)
https://en.wikipedia.org/wiki/Anderson_Gray_McKendrick

Kermack-McKendrick Model//mathworld.wolfram.com
https://mathworld.wolfram.com/Kermack-McKendrickModel.html

pathogen evolution, genomics, and biophysics//neherlab.org
https://neherlab.org

Тамм Михаил: В Москве ввели жесткие карантинные меры. Похоже, это правильно: математическая модель показывает, что иначе могли бы погибнуть больше 100 тысяч человек.
https://meduza.io/feature/2020/03/30/v-moskve-vveli-zhestkie-karantinnye-mery-pohozhe-eto-pravilno-matematicheskaya-model-pokazyvaet-chto-inache-mogli-by-pogibnut-bolshe-100-tysyach-chelovek

Число смертей в Москве выросло в апреле почти на 20%//Ведомости, 11.05.2020
https://www.vedomosti.ru/society/news/2020/05/11/829942-v-moskve-zafiksirovali-rost-chisla-smertei-v-aprele

Сбербанк подвел итоги коронавирусного года для россиян Математическое моделирование показало 16,6 млн переболевших россиян
https://www.rbc.ru/society/25/12/2020/5fe4ede99a794797d0ce9aec?from=column_8

§132.

[329] Меледин1983: Меледин Г.В. Задачи-оценки.//Квант. N7. 1983. с.26-31,62.
http://kvant.mccme.ru/1983/07/zadachi-ocenki.htm

#338 1. Оцените давление шариковой ручки на бумагу при письме.
[Меледин1983]

#339 2. Оцените скорость струи пара, выходящего из носика кипящего чайника.
[Меледин1983]

#340 3. Оцените, во сколько раз в погожий солнечный день светлее, чем ночью в полнолуние.
[Меледин1983]

#341 4. Оцените, на сколько дальше упадет граната, если спортсмен будет бросать ее с разбега.
[Меледин1983]

#342 5. Оцените время разрядки металлического заряженного шара, соединенного землей через резистор с известным сопротивлением.
[Меледин1983]

#343 6. Оцените минимальную температуру, до которой должен нагреться стакан, чтобы в него после остывания оказалась втянутой вся вода из тарелки.
[Меледин1983]

#344 7. Оцените частоту звука, генерируемого летящим комаром.
[Меледин1983]

#345 8. Оцените время, через которое вы услышите гром после вспышки молнии, если известно, что молния ударила в дерево находящееся от вас на расстоянии около 3 км.
[Меледин1983]
{Решение очень сложное, хотя, очевидно, что при скорости звука 300 м/c время составит около 10с.}

Задачи для размышлений, а решения на с.62:
http://kvant.mccme.ru/1983/07/otvety_ukazaniya_resheniya.htm

#346 1. Оцените, как изменится давление атмосферы, если вся вода в океанах испарится.
[Меледин1983]

#347 2. Оцените скорость опускания парашютиста с открытым парашютом.
[Меледин1983]

#348 3. Оцените среднюю плотность Солнца.
[Меледин1983]

#349 4. Оцените, сколько оборотов (кувырков) совершит автомобиль, на полной скорости свободно упавший в километровую пропасть.
[Меледин1983]

#350 5. Оцените усилие спортсмена при толкании ядра.
[Меледин1983]

#351 6. Оцените силу натяжения цепи велосипеда при езде в гору.
[Меледин1983]

#352 7. Оцените, с какой скоростью летеля капля воды, если при ударе о неподвижную стенку она оказывает на нее среднее давление порядка 10^8 Па.
[Меледин1983]

#353 8. Оцените силу натяжения ремней безопасности, удерживающих человека в автомобиле, если автомобиль, движущийся со скоростью порядка 30 км/ч, столкнулся со столбом, в результате чего у автомобиля получилась вмятина глубиной порядка 30 см.
[Меледин1983]

#354 9. Оцените, на сколько отличается расстояние уровней мирового океана до центра Земли на полюсе и на экваторе.
[Меледин1983]

#355 10. Оцените, на каком расстоянии человек в яркой одежде, уходя в сосновый лес, потеряется из виду. (Подлеска нет.).
[Меледин1983]

[330] Меледин1979: Меледин Г.В. Можно ли проверить ответ?//Квант. N7. 1979. с.41-43.
http://kvant.mccme.ru/1979/07/mozhno_li_proverit_otvet.htm

§133.

[331] Брук_Стасенко1981: Брук Ю., Стасенко А. Метод размерностей помогает решать задачи.//Квант. N6. 1981. с.11-19.
http://kvant.mccme.ru/1981/06/metod_razmernostej_pomogaet_re.htm

[332] Компанеец1975: Компанеец А.С. Размерность физических величин и подобие явлений.//Квант. N1. 1975. с.9-17.
http://kvant.mccme.ru/1975/01/razmernost_fizicheskih_velichi.htm

[333] Кришталь1975: Кришталь Н.Д. Метод размерностей.//Квант. N1. 1975. с.18-21.
http://kvant.mccme.ru/1975/01/metod_razmernostej.htm

§134.

Потолок Перельмана Я.И.

Самым интересным экспонатом в павильоне был его... потолок.

На темно-синем фоне ярко желтели небольшие, с двухкопеечную монету, кружочки. В центре потолка выделялась белая окружность, внутри которой находилось некоторое количество таких же золотистых горошин.

Что все это означало?

Это был один миллион. Миллион, подсчитанный, отмеренный, обозримый глазом, состоящий из отдельных, поддающихся счету единиц. Миллионы попадаются нам на каждом шагу: книга объемом в 25 авторских листов – это, как правило, миллион типографских знаков; три с небольшим года – это миллион секунд; тонна – миллион граммов; километр – миллион миллиметров... Но поди отдели один миллиметр от другого или грамм от другого грамма! А тут наглядный, осязаемый и уже тем самым занимательный миллион.

Большая часть посетителей сравнивала множество желтых кружочков на темно-синем фоне потолка с «бесчисленным множеством» звезд на небе. Чтобы поразить воображение людей, вступавших в павильон, подлинное число видимых простым глазом звезд на одном полушарии неба обвели белой окружностью. Еженощно над головами мы видим всего лишь около 2 500 звезд до 6-й величины включительно. Такое же число кружочков – одна четырехсотая часть их общего количества на потолке – и выделяла обрисованная на нем окружность.

Потолок-«миллионник» производил большое впечатление. Недоумение посетителей сменялось недоверием, переходившим в любопытство, а затем в радость узнавания. Миллион – величина отвлеченная, часто произносимая и в то же время недоступная живому восприятию – представала в павильоне как вполне ощутимая величина.

Как изготовили «миллионный» потолок?

Было бы нелепо заставить маляра накрашивать на синем фоне потолка миллион желтых кружочков. Даже по минуте на пятно – уже почти полтора года работы. Яков Исидорович поступил иначе. По его совету заказали обои – синие в золотистый горошек. В заказе говорилось: обоями нужно оклеить 250 квадратных метров поверхности потолка. На каждом квадратном метре должно быть ровно 4 000 горошин. Отпечатать на фабрике с помощью клише нужное количество обоев не составило труда.

Так был осуществлен необычный замысел Перельмана – показать воочию, что такое один миллион.

[Мишкевич1986p146-147]

[334] Мишкевич1986: Мишкевич1986: Мишкевич Г.И. Доктор занимательных наук (Жизнь и творчество Якова Исидоровича Перельмана). - М: Знание, 1986. - 192с.+8с. вкл.
http://n-t.ru/ri/ms/dz.htm

#356 Имеется квадратный лист миллиметровой бумаги в 1 метр ширины. Сколько времени понадобится, чтобы проставить точки в каждой клетке этого листа, полагая по одной точке в секунду и работая непрерывно 8 часов в сутки?

Решение. Около месяца! (Миллион точек — миллион секунд; в сутках же всего 86 400 секунд)
[Перельман1923p125]

§135.

[335] ОстровОшибок1955: Остров ошибок: Мультфильм. Режиссеры Валентина и Зинаида Брумберг. - М: СоюзМультфильм, 1955. - 26 мин. 36 сек.
https://ru.wikipedia.org/wiki/Остров_ошибок

https://www.youtube.com/watch?v=qISyHxPnuOc

[336] Вольпин2005: Вольпин М., Эрдман Н. Остров ошибок. М: Стрекоза-Пресс , 2005. - 64с.

{Двойки появляются в виде черных лебедей (может быть синих). Такие вполне себе черные лебеди от Талеба.
Послал в детстве открытку на телевидение, с просьбой повторить этот мультфильм. Ответ пришел на youtube =:)}

§136.

Формула Карбышева: один батальон, один час, один километр, одна тонна, один ряд.

Особой, как мне кажется, популярностью пользовался в нашей слушательской среде Дмитрий Михайлович Карбышев, ученый-инженер, умевший преподнести свой, казалось бы, «сухой» предмет очень остроумно, оригинальными и простыми методами помогавший нам запоминать сложные технические расчеты. На всю жизнь запала в память его практическая формула расчета сил и средств при оборудовании позиций заграждениями из колючей проволоки: один батальон, один час, один километр, одна тонна, один ряд. Шутники - острословы переиначили ее: один сапер, один топор, один день, один пень. Шутка дошла до Карбышева и нисколько не обидела его. Он и сам при случае не упускал возможности пошутить. Пожалуй, ни одна из его лекций не обходилась без этого.

[Штеменко С.М. Генеральный штаб в годы войны
http://militera.lib.ru/memo/russian/shtemenko/01.html]

[337] Штеменко:Генеральный штаб.2005: Штеменко С.М. Генеральный штаб в годы войны. . - М.: Воениздат, 1989.
http://militera.lib.ru/memo/russian/shtemenko/index.html

{Согласно формуле на 1 метр заграждений приходится 1 кг колючей проволоки. Немного поискав в интернете, можно найти, что бухта весом 10 кг содержит 90 погонных метров проволоки. В этом случае на 1 метр заграждений придется 9 погонных метров проволоки, что, похоже, позволит создать надежную защиту.}

Проволока колючая ГОСТ 285-69 от производителя г. Екатеринбург:
http://mi96.ru/provoloka_kolyuchaya_gost_285-69

Карбышев Дмитрий Михайлович (1880-1945)
https://ru.wikipedia.org/wiki/Карбышев,_Дмитрий_Михайлович

[338] Карбышев1936: Карбышев Д.М. Краткий справочник по военно-инженерному делу : Для тактических занятий. Заграждения: Устройство, боевое применение, разведка и преодоление заграждений. - М: Гос. воен. изд-во, 1936. - 272 с. - (Библиотека командира).

[Карбышев1936p108]

[Карбышев1936p113]

§137.

Попробуйте смешать спирт и воду. Получите теплую жидкость, похожую на водку. Только из 1 литра спирта и 1 литра воды получится совсем не 2 литра водки.

Менделеев Дмитрий Иванович (Dmitri Mendeleev)(1834-1907)
https://ru.wikipedia.org/wiki/Менделеев,_Дмитрий_Иванович

[339] Менделеев1865: Менделеев Д.И. Рассуждение о соединении спирта с водой, представленное в Физико-математический факультет И. С.-Петербургского университета Д. Менеделеевым для получения степени доктора химии. - Санкт-Петербург : тип. т-ва "Обществ. польза", 1865. - 120 с.
https://rusneb.ru/catalog/000199_000009_003567719/viewer/?page=3

https://dlib.rsl.ru/viewer/01003567719?login=1#?page=1

[340] Менделеев1865: Менделеев Д.И. О соединении спирта с водой / [Соч.] Д. Менделеева. - Санкт-Петербург : Обществ. польза, 1865. - 119 с.
https://dlib.rsl.ru/viewer/01003567718?login=1#?page=1

Шипилов А. Что было в диссертации Менделеева "О соединении спирта с водою"
https://pikabu.ru/story/chto_byilo_v_dissertatsii_ mendeleeva_o_soedinenii_spirta_s_vodoyu_280965

[341] Григорьева2010: Григорьева В.З. Русская водка: всегда ли было 40%.//Химия и жизнь, 2010, N 5.
https://hij.ru/read/issues/2010/may/960/

Менделеев и бездымный порох.

Менделеев берет статистические отчеты железных дорог Франции и погружается в их изучение. Он делает простое предположение: запасов химического сырья на заводах не образуется. Годовой подвоз в среднем целиком идет в производство. Следовательно осталось подсчитать, сколько перевозится за год по заводской железнодорожной ветке:
эфира,
серной кислоты,
азотной кислоты,
хлопка.

Сделав необходимые подсчеты, Менделеев выводит, наконец, необходимое для его задачи числовое отношение эфира к пироколлодию.

Задача решена - и Менделеев возвращается, посмеиваясь добродушно, в Россию, где успешно заканчивает свою работу.

[Святловский.Занимательная статистика.1933 ,с.5]

[342] Святловский1933: Святловский Е.Е. Занимательная статистика. - Л: Кооперативное издательство "Время", 1933. - 240с. - Тираж 10000.

Все очень интересно и в тему, но было совсем не так:

[343] Дмитриев1996: Дмитриев И. С. "Особая миссия" Менделеева: факты и аргументы// ВИЕТ № 3, 1996
http://vivovoco.astronet.ru/VV/PAPERS/HISTORY/VV_HI2_W.HTM

Менделеев и Академия Наук

[344] Дмитриев2003: Дмитриев И.С. Скучная история. (о неизбрании Д. И. Менделеева в Императорскую академию наук в 1880 г.) //ВИЕТ. 2003. Т. 23. № 2. С. 231–280
http://old.ihst.ru/viet/2002(2)/2002_2_html/Dmitriev(1).htm

Таблица Менделеева.
https://www.artlebedev.ru/mendeleev-table

§138.

Елькин Виктор Иванович (1952 – 2007)
https://elkin-andrey.ru/el-kin-viktor-ivanovich

[345] Елькин2003: Занимательная физика в вопросах и ответах. Сайт Елькина Виктора. (Заслуженный учитель РФ. Учитель-методист.)
http://www.elkin52.narod.ru

[346] Елькин1998: Елькин В.И., Елькин А.В. Определение роста человека с помощью часов (9 класс) // Приложение к газете «Первое сентября». «Физика». 1998, № 8. С. 11

#357 Определение роста человека с помощью часов.
https://nsportal.ru/shkola/fizika/library/2013/02/02/prakticheskie-raboty-dlya-uchashchikhsya-8-klassa

[347] Елькин2001: Елькин В.И. Необычные учебные материалы по физике / Сост. Э.М.Браверман. – М.: Школа-Пресс, 2001. – 80 с. – (Библиотека журнала “Физика в школе”. Вып. 24. Кн.1).

[348] Елькин2001: Елькин В.И. Оригинальные уроки физики и приемы обучения / Сост. Э.М.Браверман. – М.: Школа-Пресс, 2001. – 80 с. – (Библиотека журнала “Физика в школе”. Вып. 24. Кн.2).

[349] Елькин2003: Елькин В.И., Гармаш Л.Д., Браверман Э.М. Физика и астрономия в походе и на природе / Сост. и ред. Э.М. Браверман. – М.: Школьная Пресса, 2003. – 96 с. (Библиотека журнала “Физика в школе”, – Вып. 25).

§139.

Потери в Великой Отечественной войне.

Подробная статья в Википедии с источниками:
https://ru.wikipedia.org/wiki/Потери_в_Великой_Отечественной_войне

[350] Земсков2013: Земсков В.Н. О масштабах людских потерь CCCР в Великой Отечественной Войне (в поисках истины) // «Военно-исторический архив», 2012, №9, с. 59-71. (28 ссылок на источники)
http://www.demoscope.ru/weekly/2013/0559/analit01.php

[351] Ивлев2012: Ивлев И. Генеральская ложь //Опубликовано в журнале «Военно-исторический архив», 2012, №9, с. 41-58.
http://www.demoscope.ru/weekly/2013/0559/analit02.php

Оценка разницы дисбалансов между мужчинами и женщинами по возрастам 1886-1927 г.р. в 1939 и 1946 гг.

[352] Богоявленский2013: Богоявленский Д. Еще раз о потерях в Великой отечественной войне: историкам о демографии.
http://www.demoscope.ru/weekly/2013/0559/analit03.php

...все расчеты были и выполнены группой сотрудников отдела демографии НИИ Госкомстата СССР (другого подразделения этого ведомства) Е.М. Андреевым, Л.Е. Дарским, Т.Л. Харьковой. (В дальнейшем я буду использовать общепринятое в литературе сокращение АДХ).

1. Одним из первых сделал сходную оценку, исходя только из предварительных результатов переписи 1959 г., американский экономист Исон (Eason), написав буквально: «Другими словами, война ответственна за смерть приблизительно 25 млн. человек из населения, жившего в 1940 г.» Первые итоги переписи 1959 г., были напечатаны в центральных советских газетах в мае того же года, а Исон опубликовал свою оценку уже в июле.

2. В 1989 г. демограф С. Максудов опубликовал свой расчет военных потерь: потери 24,5 млн (18,7 млн мужчин и 5,8 млн женщин). При этом интервал точности расчета он определил от 21 до 29 млн. Автор – эмигрировавший диссидент, поэтому не боялся идти вразрез с официальными тогда двадцатью миллионами, и не дожидался, чтобы первое слово произнес генсек.

3. В 1992 г. пермский демограф В.С. Гельфанд, опираясь, в отличие от АДХ, на некорректированные данные советской статистики, определил общее число погибших из-за войны – 26,4 млн.

[353] Богоявленский2012: Богоявленский Д. Как утаивали величину военных потерь
http://www.demoscope.ru/weekly/2012/0513/arxiv01.php

{Письмо начальника ЦСУ СССР В.Старовского в ЦК КПСС, 14.11.1956}

[354] Тарасов2011: Тарасов В.П. Потери СССР в годы Второй мировой войны: современное состояние проблемы// Доклад Заместителя руководителя Федерального архивного агентства В.П.Тарасова на международной конференции (г. Будапешт (Венгрия), 9–10 декабря 2011 г.)
http://archives.ru/reporting/report-tarasov-2011-budapest.shtml

[355] Кривошеев1993: Кривошеев Г.Ф., ред.: Гриф секретности снят. Потери вооруженных сил СССР в войнах, боевых действиях и боевых конфликтах. Статистическое исследование. - М: Воениздат, 1993. - 415 с.

[356] Кривошеев2001: Г.Ф.Кривошеев (под редакцией). Россия и СССР в войнах XX века: Потери вооруженных сил. Статистическое исследование. Под общей редакцией кандидата военных наук, профессора АВН генерал-полковника Г. Ф. Кривошеева. М: ОЛМА-ПРЕСС, 2001.
http://lib.ru/MEMUARY/1939-1945/KRIWOSHEEW/poteri.txt

[357] ВОВ2015: Великая отечественная война. Юбилейный статистический сборник: Стат.сб./Росстат. - М: 2015. - 190с.
http://www.gks.ru/free_doc/new_site/pobeda70/vov_svod_1.pdf

[358] Рыбаковский2010: Рыбаковский Л. Л. Людские потери СССР и России в Великой отечественной войне. — М.: Экон-Информ, 2010. — 140 с.
http://militera.lib.ru/research/0/pdf/rybakovsky_ll01.pdf

[359] Соколов2011: Соколов Б.В. Потери Cоветского Cоюза и Германии во второй мировой войне: методы подсчетов и наиболее вероятные результаты// Серия "АИРО - научные доклады и дискуссии Темы для XXI века". Выпуск 29. - М: АИРО-ХХI, 2011. - 128с.
http://www.demoscope.ru/weekly/2011/0461/biblio04.php

§140.

Фотоны. Такие фотоны.

Сколько фотонов способен различить глаз?
https://www.nkj.ru/facts/29236

Таким образом, получается, что человек способен различить 1 фотон.
Мощность излучения Солнца на орбите Земли составляет 1370 Вт/кв.м.
Энергия одного фотона F=4e-19 Дж
Разделив одно на другое, получим количество фотонов на 1 кв.м.: 3.4e26
Или 3.4e17 штук на см**2
На какое расстояние нужно удалиться, чтобы остался 1 фотон на см**2? Человеческий глаз имеет немного большие размеры, но это оценка.
Площадь сферы S =4*Pi*R**2
Мы должны уменьшить количество фотонов в 3.4e17 раз, для это необходимо отодвинуть границу в sqrt(3.4e17)=sqrt(34)*1e16 = 6e8 (это приблизительно).
Отодвигаем границу на 6e8=600 млн. астрономических единиц (расстояний от Земли до Солнца)
Одна астронимическая единица равна 150 млн.км=1.5e8 км.
1.5e8*6e8 = 9e16 км.
Оценим данное выражение в световых годах:
9e16/(300000*60*60*24*365) = 9500 световых лет.
То есть звезда (с параметрами Солнца) излучает такое количество фотонов, что на сфере с радиусом 9500 световых лет приходится по одному фотону на 1 кв.см.

§141.

[360] Васильев2019: Васильев Артём: Сколько человек на самом деле живет в Москве? Сравниваем официальные и неофициальные данные.//Банки Сегодня,11.10.2019
https://bankstoday.net/last-articles/skolko-chelovek-na-samom-dele-zhivet-v-moskve-sravnivaem-ofitsialnye-i-neofitsialnye-dannye

[361] Махрова_Бабкин2018.BC: Махрова А. Г., Бабкин Р. А. Анализ пульсаций системы расселения Московской агломерации с использованием данных сотовых операторов //Региональные исследования. — 2018. — № 2 (60). — С. 68–78.
https://istina.msu.ru/publications/article/133260490

Москва. 12.6 млн. человек. 01.01.2020.
Согласно данным управления Росстата по Москве, по состоянию на 1 января 2020 года численность населения столицы составляет 12,6 млн человек.
https://www.rbc.ru/society/02/05/2020/5ead0c219a79472412911f14?from=from_main

Управление Росстата по Москве
https://mosstat.gks.ru/folder/64634

§142.

[362] Mitchell2012: Michael Mitchell: A clever way to estimate enormous numbers.2012:
https://www.youtube.com/watch?v=0YzvupOX8Is

§143.

Задача Ильфа и Петрова.

По сборнику путевых заметок «Одноэтажная Америка». 1935-1936гг.
Какой расход бензина у благородного мышиного форда? [Гл.10] Мистер Адамс забыл шляпу. Почему не выгодно возвращаться. [Гл.14]

Наш благородный мышиный форд показал, что расходует на каждые шестнадцать миль один галлон бензина. В штате Нью-Йорк бензин стоит шестнадцать центов за галлон. Значит, полный бак в четырнадцать галлонов стоимостью в два доллара двадцать четыре цента давал нам возможность сделать двести двадцать четыре мили.
[Ильф_Петров2018p82]

Какой расход бензина у «благородного мышиного форда» в обычных единицах измерения, литрах на 100 км?
Для ответа на данный вопрос галлоны требуется перевести в литры, мили - в километры и пересчитать результат в расчете на 100км.
Если призвать на помощь Google, то можно узнать, что
1 галлон = 3.785 литра,
а 1 миля = 1.785 км.

Составим пропорцию:
(16 * 1.6) км - 3.785л
100 км - x
Откуда x = 3.785*100/25.6 = 14.8 л/100 км.

Попутно можно узнать стоимость бензина в Америке в конце 1935г. (0.04 цента/литр) и емкость бака данного Форда в литрах (53л). На полном баке можно проехать где-то 358 км. Что составляет 223.8 миль. 0.2 мили съела погрешность вычислений.

Мистер Адамс забыл шляпу в Скенектеди. И уехал на 30 миль. И вот как он рассуждает: лучше всего это покажет прямая цитата:

Но, сэры, - сказал мистер Адамс, уже оправившийся от потрясения, - это будет легкомысленный поступок, если мы вернемся в Скенектеди. Да, да, сэры. Будет ли этот поступок достаточно разумным? Моя шляпа стоила четыре доллара в девятьсот тридцатом году. Плюс чистка в девятьсот тридцать третьем году - пятьдесят центов. Итого - четыре доллара пятьдесят центов. Мистер Адамс вынул карандашик и блокнот и принялся калькулировать. - Моя шляпа, сэры, в ее теперешнем состоянии стоит не больше полутора долларов. До Скенектеди и обратно - шестьдесят миль. Наш кар делает на один галлон бензина в среднем шестнадцать, ну, скажем, пятнадцать миль. Итого - нам надо затратить четыре галлона по шестнадцать центов за галлон. Всего шестьдесят четыре цента. Теперь надо принять во внимание амортизацию автомобиля, расходы на масло и смазку. Серьезно! О, но! Было бы глупо возвращаться в Скенектеди за шляпой.
[Ильф&Петров2018, гл.14, c.109-110]

[363] Ильф_Петров2018: Ильф И., Петров Е. Собрание сочинений: в 5т. - СПб: Издательство Пальмира, М: ООО Книга по требованию, 2018. Т.4: Одноэтажная Америка. - 482с.

§144.

ГоловоЛомкА БигСова: Математическая головоломка Если вы нашли решение, то ваш IQ точно выше среднего.
zen.yandex.ru

{На странице не хватит полей, чтобы полностью отобразить ссылку на zen.yandex.ru. Кстати, как показывает практика, ссылка не долговечная и может внезапно пропасть. Тогда исходный источник придется искать по ключевым словам или в Web.Arhive, если он еще туда попадет.}

Зная немного о простых числах, можно решить методом подбора. В комментариях приведена программа на Python, надо организовать 2 цикла. На Excel можно сделать нагляднее: по вертикали х, по горизонтали y, на пересечении:
x³-y³-721
Образец формулы: =$A10*$A10*$A10-G$1*G$1*G$1-721
По диагонали всегда будет -721.
Там, где ноль, там правильный ответ:
x=9, y=2
x=16, y=15

§145.

Задача У.Баффета и индейцы.

Приводя пример силы сложных процентов, У. Баффет сказал в 1969 году [Торп2017p237p533]:

Если бы манхеттенские индейцы могли бы инвестировать 24 доллара - стоимость тех безделушек, за которые они отдали Манхеттен Петеру Минёйту, - под 8% чистой прибыли, то сейчас они могли бы снова выкупить весь остров со всем, что на нем было построено.

Комментарии Торпа[Торп2017p237p533]:
Петер Минёйт (нидерл. Peter Minuit) (1580-1638) губернатор голландских колоний в Америке. В 1826 году купил остров Манхеттен у местного племени, обменяв на бусы общей стоимостью 60 голландских гульденов. Считается, что это составляет 24 доллара США.
Петер Минёйт в 1631 г. по неизвестной причине был отозван Голландской Вест-Индской компанией в Европу, наверное, там сочли, что он переплатил индейцам.
Расчет строится на основании того, что между 1626 и 1968 гг. прошло 342 года. при приросте в 8% годовых 24 доллара превратились бы в 6.47 триллиона долларов, что составляет 1/8 активов США на тот момент. К 2013г. восьмипроцентный рост дал бы 206 триллионов долларов. Чистая стоимость активов США в 2013г. - около 100 триллионов долларов, а США имеют 25% активов мира.

Проблема только в том, что обеспечить восьмипроцентный рост на столь длительный период малореально.
А 5-ти процентный рост дает только 423 млн. долларов,
а 3-x - 589 тыс.
Рост в 1% принесет индейцам только 721 доллар.

Формула: New = Old (1+ 0.01x%)years, и считать через логарифм.

[Торп2017p237p533]
[Thorp2017p157]
[Четыркин2000p45] (Хватит и 6.3% годовых)
[Posamentier2018p100]

Уоррен Эдвард Баффетт (Warren Edward Buffett) (1930-)
https://ru.wikipedia.org/wiki/Баффетт,_Уоррен

Эдвард Торп (Edward Oakley Thorp)(1932-)
https://ru.wikipedia.org/wiki/Торп,_Эдвард

Момент покупки Манхэттэна отражен на картине Alfred Fredericks(1835-1926).The Purchase of Manhattan Island.1910.
https://commons.wikimedia.org/wiki/File:The_Purchase_of_Manhattan_Island.png
https://www.britannica.com/place/Manhattan-New-York-City

Другие иллюстрации данного события:
Peter A. Douglas Illustrating The Manhattan Purchase.
https://www.newnetherlandinstitute.org/history-and-heritage/additional-resources/illustrating-the-manhattan-purchase/

§146.

Задача о разборчивой невесте.

Примерно 40 лет тому назад М. Гарднер придумал такую задачу: В некотором царстве, в некотором государстве пришло время принцессе выбирать себе жениха. В назначенный день явились 1000 царевичей. Их построили в очередь в случайном порядке и стали по одному приглашать к принцессе. Про любых двух претендентов принцесса, познакомившись с ними, может сказать, какой из них лучше. Познакомившись с претендентом, принцесса может либо принять предложение (и тогда выбор сделан навсегда), либо отвергнуть его (и тогда претендент потерян: царевичи гордые и не возвращаются). Какой стратегии должна придерживаться принцесса, чтобы с наибольшей вероятностью выбрать лучшего?
[Гусейн-Заде2003:Из аннотации.]

[364] Гусейн-Заде2003 Гусейн-Заде С.М. Разборчивая невеста. — МЦНМО, 2003. — Т. 25. — 20 с.
https://www.mccme.ru/mmmf-lectures/books/books/book.25.pdf

[365] Луридас.Алгоритмы.2018 Луридас Панос: Алгоритмы для начинающих: теория и практика для разработчика. - М: Эксмо (Бомбора), 2018. - 608с. - Доп. тираж 2000.
Ориг. назв.: Panos Louridas: Real-World Algorithms. A Beginner's Guide. The MIT Press. 2017.

У задачи о разборчивой невесте интересная история: впервые ее напечатали в феврале 1960 года в журнале Scientific American, в рубрике Мартина Гарднера, решение же напечатали в марте 1960 года; посмотрите доклад Фергюсона [Ferguson.SecretaryProblem.1989], где он указывает, что подобные задачи восходят к Кеплеру. Решение варианта, где все кандидаты рассматриваются согласно их достоинствам, было дано Бирденом [Bearden2006].
[Луридас2018p340]

Gardner Martin: Mathematical Games. A fifth collection of "brain-teasers"//Scientific American. 1960.Feb:150-154.

Gardner Martin: Mathematical Games. The games and puzzles of Lewis Carroll, and the answers to February's problems.//Scientific American. 1960.Mar:172-182.

Игра в гугол имеет много интересных применений. Вот, например, одно из них. Девушка решает выйти замуж до конца года. Она надеется, что ей удастся встретить десять человек, которые сделают ей предложение (получив отказ, каждый из претендентов на ее руку не проявляет особой настойчивости и от дальнейших попыток добиться согласия своей избранницы отказывается). Какой стратегии следует ей придерживаться, чтобы увеличить свои шансы выбрать самого достойного из женихов? С какой вероятностью она добьется успеха? Оптимальная стратегия состоит в том, чтобы, отвергнув некоторое число листков бумаги (или предложений), выбрать следующее число, которое превосходит наибольшее из отвергнутых чисел. Требуется найти лишь формулу, которая бы показывала, сколько листков следует отбросить в зависимости от полного числа листков.

[Гарднер1971p372-373]

[366] Гарднер1971 Гарднер М. Математические головоломки и развлечения. - М: Мир, 1971. - 511с.
Ориг. Назв.: Martin Gardner: Mathematical Puzzles and Diversions. London: Bell and Sons.

[367] Ferguson1989 Who Solved the Secretary Problem?//Statistical Science. 1989. Vol. 4, No. 3, 282-296.
https://projecteuclid.org/download/pdf_1/euclid.ss/1177012493

Кандидаты оцениваются согласно их достоинствам [Луридас2018p319].

[368] Bearden2006 J. Neil Bearden: A new secretary problem with rank-based selection and cardinal payoffs, Journal of Mathematical Psychology, Volume 50, Issue 1, 2006, Pages 58-59
https://doi.org/10.1016/j.jmp.2005.11.003.
http://www.sciencedirect.com/science/article/pii/S0022249605000933

[369] Dunkin1963 Dunkin E.B. 1963 The optimun choice of the instant for stopping a Markov process. Soviet Math. Dokl. 4 627-629.

Мостеллер1971p20_Задача47.

[370] Мостеллер1971 Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. - М: Наука, 1971. - 104с.
Ориг. назв.: Frederick Mosteller: Fifty Challenging Problems in Probability: With Solutions. 1988. - 88 p.
https://www.mathedu.ru/text/mosteller_50_zanimatelnyh_veroyatnostnyh_zadach_1975/p0/

[371] Березовский1983 Березовский Б.А. Разработка теоретических основ алгоритмизации принятия предпроектных решений и их применения : Автореф. дис. на соиск. учен. степ. д. т. н. - М., 1983. - 38 с. - Список работ авт.: с. 36-38

Кристиан_Гриффитс2017p19-48
Задача об оптимальной остановке. Когда пора остановить поиски. 37% (Optimal stopping)

[372] Hill2009 THEODORE P. HILL (Теодор Хилл) Knowing When to Stop. How to gamble if you must—the mathematics of optimal stopping//American Scientist, MARCH-APRIL 2009, VOLUME 97, NUMBER 2,PAGE 126.
https://www.americanscientist.org/article/knowing-when-to-stop

Википедия, особенно английская, содержит большое количество ссылок:

https://ru.wikipedia.org/wiki/Задача_о_разборчивой_невесте

https://en.wikipedia.org/wiki/Secretary_problem

Стратегия разборчивой невесты.
[Хургин1977p63-67]

§147.

Кувшин Абдуллы.

Вечерело. Уставший за нелёгкий день бедный рыбак Абдулла присел на берегу реки отдохнуть. Вдруг видит плывёт по волнам какой-то предмет, почти полностью погружённый в воду, только самый краешек виден на поверхности воды. Абдулла бросился в реку и вытащил его. Смотрит, а это старинный глиняный кувшин, с горлышком плотно закрытым пробкой и залитым сургучом. Распечатал Абдулла кувшин и обомлел: из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а кувшин закрыл, залил горлышко сургучом и бросил обратно в реку. И поплыл кувшин дальше, примерно на треть выступая над водой — так говорится в одной из восточных сказок.

Полагая, что кувшин был двухлитровым, оцените массу одной монеты. (Задача давалась на Областной олимпиаде школьников, 2004, Тюм. обл.)
[Габышев2012p11]

2/(3*147) = 4.5 г, что соответствует реальному весу монет.

2 - кувшин был двухлитровым,
1/3 - монеты весили как вода, вытесенная третьей частью кувшина, 147 - количество монет.

[373] Габышев2012: Габышев Дмитрий Николаевич. Искусство составлять задачи и немного об их решении: учебное пособие / Д. Н. Габышев ; Российская Федерация. М-во образования и науки, ФГБОУ ВПО Тюменский гос. ун-т, Ин-т математики, естественных наук и информ. технологий. - Тюмень : ТюмГУ, 2012. - 67 с. Библиогр (49 назв.) с.68-73.
https://docplayer.ru/63904620-Iskusstvo-sostavlyat-zadachi.html

§148.

Прачечная? ... Министерство культуры
https://www.anekdot.ru/id/-10087716

Сколько прачечных в Москве?
https://mathreshka.medium.com/solution-laundry-guess-65-605fefd5af2c

Напрашивается следующий вопрос:
Сколько министерств культуры в Москве?
Три? России, Москвы (департамент можно считать министерством?), Московской области.

§149.

Если монетка попалась кривая...

Задача фон Неймана: Как бросить жребий кривой монетой?
[Paulos2001p29]
Надо бросить монету дважды. Если выпадут два орла или две решки, то надо повторить. Если выпадет последовательность орел-решка, то победила первая сторона, если решка-орел, то вторая.

Честная игра с нечестной монетой.
https://telegra.ph/Reshenie-CHestnaya-igra-s-nechestnoj-monetoj-13-12-14

Как честно поделить одно место между тремя попутчиками с помощью кривой монетки?
[Gowers2012p42]

§150.

13 шаров Касперского.

На столе 13 шаров. Один шар другого веса — по отношению к остальным 12-ти шарам (легче или тяжелее — неизвестно, просто другой). На столе весы (больше-меньше). Задача. За три (только три!) взвешивания определить «неправильный» шар.
https://eugene.kaspersky.ru/2020/04/02/48078

Две монетки. Одно взвешивание. Легче и тяжелее неизвестно. Сравнение с эталоном.
Три монетки. Одно взвешивание. Легче или тяжелее известно. Одну откладываем, две на весы.
Пять монеток. Два взвешивания. Две откладываем. Три взвешиваем с тремя эталонами. Легче или тяжелее неизвестно.
Тринадцать монеток. Три взвешивания. Пять откладываем. 4+4.
Восемь монеток. Четыре условно легких. Четыре условно тяжелых.
Откладываем 3 тяжелых. Осталось 4 легких и 1 тяжелая.
Тяжелую перекладываем на чашку с легкими, два легких - на чашку тяжелых. Добавим эталон.
Если весы в равновесии - фальшивка среди трех отложенных тяжелых. За один раз.
Если весы указывают на ту же чашку, то фальшивка среди двух легких, которые не двигали.
Если поменяли, то среди передвинутых 2 легких и 1 тяжелой. Легкие на весы. Тяжелый в остатке.
Вроде все сошлось.
Хотелось бы найти решение в системе счисления с основанием 3, но как-то не идет в голову.

[374] Кноп2016:
Кноп К.А. Взвешивания и алгоритмы: от головоломок к задачам. - М: МЦНМО, 2016. - 104с.

В конце статьи много источников:
Tanya Khovanova (MIT): Parallel Weighings
https://arxiv.org/pdf/1310.7268.pdf

[375] Шестопал1979: Шестопал Г. Как обнаружить фальшивую монету.//Квант. 1979. N 10. с.21-25.
http://kvant.mccme.ru/1979/10/kak_obnaruzhit_falshivuyu_mone.htm

§151.

[376] Перельман1923: Перельман Я. И. Практические занятия по геометрии. Образцы, темы и материалы для упражнений. - М-Петроград: Государственное издательство, 1923. - 176с.
http://publ.lib.ru/ARCHIVES/P/PEREL'MAN_Yakov_Isidorovich/_Perel'man_Ya.I..html#0042

Перельман Яков Исидорович (Yakov Perelman) (1882-1942)
https://ru.wikipedia.org/wiki/Перельман,_Яков_Исидорович
«Родился я в городе Белостоке»
http://n-t.ru/ri/ms/dz02.htm
Работа в журнале Природа и Люди.

[377] Перельман1911: Перельман Я.И. Как составляется и печатается журнал "Природа и люди"//Природа и люди, 1911, № 3, с.40-44. Вырезка.

Занимательная физика.
Работы по звездоплаванию.
Идея декретного времени
Крупская Н.К. В Мастерской природы.
Кооперативное издательство Время.

[378] Маликова2011: Маликова М.Э. Шум времени: История ленинградского кооперативного издательства «Время» (1922–1934)// http://www.pushkinskijdom.ru/LinkClick.aspx?fileticket=Bv_Fk5a7yiE%3d&tabid=10460

«Занимательная наука» (Я.И.Перельман) [Маликова2011p78-83]

Дом Занимательной науки. ( 15 октября 1934 - 29 июня 1941) Фонтанка,34.

Адрес проживания: Плуталова, 2. Кв.12. Количество ступенек. «Я живу на 2-м этаже, лестница с 20 ступеньками» [ПерельманАрифм_p184]

1 августа 1934 года – в составе группы ленинградских писателей и ученых-популяризаторов встретился с Гербертом Уэллсом, приезжавшим в СССР. Мишкевич Г.И. на встрече присутствовал и оставил полновесные заметки: Три часа у Герберта Уэллса
http://n-t.ru/ri/ms/dz07.htm

Анна Давидовна Перельман-Каминская и Яков Исидорович Перельман. май 1941 г. у дома по Плуталовой ул., 2 (Мишкевич Г.И. Доктор занимательных наук - М.: Знание, 1986.)
https://www.citywalls.ru/house880.html?s=ks2bs1g3hmhjg70ji6pt540lc0

16 марта 1942 года скончался от голода в блокадном Ленинграде.

Список работ у Мишкевича Г.И.
Основные произведения Я.И. Перельмана на русском языке:
http://n-t.ru/ri/ms/dz11.htm

§152.

Данилов Юлий Александрович (1936-2003) Институт атомной энергии им. Курчатова.
Перевел немерянное количество книг. Это Джон фон Нейман, Алан Тьюринг, Вернер Гейзенберг, Илья Пригожин, Вольфганг Паули, Альфред Реньи, Давид Гильберт, Евгений Вигнер, Георгий Гамов и Мартин Гарднер.
ru.wikipedia.org/wiki/Данилов,_Юлий_Александрович

https://web.archive.org/web/20151206112507/ http://www.synergetic.ru/people/yuliy-aleksandrovich-danilov-1936-2003.html

[379] Данилов2008: Данилов Ю.А. Прекрасный мир науки. Сборник. Сост. А.Г.Шадтина. - М: Прогресс-Традиция, 2008. - 384с.- Тираж 800.
http://www.ega-math.narod.ru/Danilov/Danilov.htm
Библиогр. с. 365-383 (176+19+11+102+107).
с. 366 Научные и научно-популярные статьи. 176 назв.
с. 374 Составление книг. 19 назв.
с. 375 Редактирование книг. 11 назв.
с. 375 Переводы научных статей. 102 назв.
с. 380 Переводы книг. 107 назв.
Полный список:
www.ega-math.narod.ru/Danilov/Danilov.htm#ch49
Копия из книги: [Данилов2008p366-383]:
Библиография работ Данилова Ю.А., pdf, 9.6 MB

[Данилов2008p2-3]

§153.

1. Задачи Арнольда

2. Задачи Перельмана:
Занимательная геометрия на вольном воздухе. Живая математика.
Занимательная механика.
Занимательная алгебра.

3. Маковецкий (§73)

4. Кордемский (§72)

5. Фрикономика (§116)

6. Фейнман

7. Талеб

8. Канеман

9. Поппер

10. Кэролл

11. Теория игр/Диксит

12. Карпушина

13. Чехов. Репетитор.
http://kolesnikov.net/Tutor.pdf

14. Канторович

15. Менделеев и бездымный порох. Переехал в параграфы. §136.

15A. Лаверье. Открытие Нептуна.

16. Бертольд Якоб.

16. Сурдин.

17. Губайловский.

18. Морз & Кимбелл.

19. Derrick Niederman.

20. Хургин.

#358 21. Сколько весит этаж небоскреба?

#359 22. Перельман и Эйфелева башня: если весь металл Эйфелевой башни расплавить и разлить по основанию, какова будет толщина слоя?
https://mi3ch.livejournal.com/2519605.html

{Ответ: основание 125*125 метров, металла  8 тысяч тонн, плотность железа 7800 кг/куб.м. Итого: на 1 метр основания приходится полтонны металла, высотой 6.5 см.}

#360 Какова высота модели Эйфелевой башни весом в 1 кг?
[БольшойПодарокЭрудиту2014, с.213]

[380] БольшойПодарокЭрудиту2014: Перельман Я.И. Большой подарок эрудиту. Что? Зачем? Почему? Занимательная физика, механика, астрономия, математика, природа. - М: АСТ, 2014. - 240с.
{Книга интересная, только Перельман Я.И. имеет к ней косвенное отношение.}

Добывание огня трением. [БольшойПодарокЭрудиту2014p63]

Задача Полет вертолета на 500 км. 4 раза. Вертолеты так далеко не летают. [БольшойПодарокЭрудиту2014p222]

"В самом деле, здесь что-то неладно". Какова дальность полета вертолета? В оригинале у Перельмана присутствует дирижабль.
[Перельман2016p14-15]

Задача Архимеда. Большой подарок эрудиту. [БольшойПодарокЭрудиту2014p238]

23. Артиллерия под ред. Внукова. (§66)

24. Задачи Капицы (§63)

25. Святловский.Занимательная статистика.1933 в п.14

26. НПФ - Нобелевская премия по физике.

27. [381] Герштейн2019: Сергей Герштейн, Анна Герштейн: Меры и веса. Онлайновый конвертер величин. Конвертировать единицы измерения? Легко! (1996-2019):
https://www.convert-me.com

28. Ian Stewart (§69)

29. Задача о трех стрелках. Труэль [Бернар Вебер] (§80)

30. Сингх (§74)

31. Генри Кавендиш (Henry Cavendish)(1731 — 1810) §77(76)

32. Скляревский Евгений Семенович (1956-): Занимательный мир чисел, слов, пикселей и заблуждений. http://www.arbuz.uz

33. Смаллиан Рэймонд (Raymond Merrill Smullyan) (1919 – 2017)
https://ru.wikipedia.org/wiki/Смаллиан,_Рэймонд_Меррилл

[382] Смаллиан1981: Смаллиан Рэймонд: Как же называется эта книга? Пер. с английского и предисл. Ю. А. Данилова. М.: Мир, 1981. — 238 с.
Ориг. назв.: Raymond Smullyan:What Is the Name of This Book? 1978.

34. Randall Munroe:

[383] Munroe2014: Randall Munroe: What if? Serious Scientific Answers to Absurd Hypothetical Questions. - Boston, New York: Houghton Mifflin Harcourt, 2014. - 304p.

[384] Манро2019.B2: Манро Р. А что, если?.. Научные ответы на абсурдные гипотетические вопросы. - М: Издательство АСТ, 2019. - 416с.

35. Теодор Хилл и монетка. (§115)

36. Количество названий книг в мире.

37. [385] Lance_Mason2019: Lance Cooper, Nadya Mason: Making Estimates in Research and Elsewhere
https://courses.physics.illinois.edu/Phys496/fa2019/Lectures/Estimates.pdf

#361 38. На какую высоту подскочит футбольный мяч, отпущенный на высоте 10м?
[Purcell1984]

39. Прыжки в высоту на Луне

Маковецкий1991p38_Задача16.

Перельман Я.И.: Занимательная механика.-Л:Время,1933: с.65-69 Семимильные сапоги (Глава 4).
На англ: Yakov Perelman: Mechanics for Entertainment. 2014: 100 yards boots (Chapter Four):
"Шар-прыгун в сложенном виде умещается в чемодане". Произведенные расчеты высоты прыжков с помощью воздушного шара, к Луне, конечно, никакого отношения не имеют, поскольку на Луне по последним данным нет воздуха, а относятся только к меньшему весу прыгуна.

[386] Попов2009: Попов А.И. Американцы на Луне. Великий прорыв или космическая афера? - М: Вече, 2009.
https://www.manonmoon.ru

Прыжки в высоту:
https://public.wikireading.ru/58107

Прыжки на Луне: Так прыгать можно и на Земле.
[Попов2009p136-138].

Расчет скорости ракеты по кадрам:
[Попов2009p233].

Опыт Галилея. Монтаж снимков в фильмах:
[Попов2009p134-136].

[387] Покровский2007: Покровский С.Г. Попасть на Луну американцы не могли//Актуальные проблемы современной науки:
http://naukarus.com/popast-na-lunu-amerikantsy-ne-mogli

Расчет скорости ракеты по ролику.

40. Эдисон нанял на работу математика, и поручил рассчитать объем колбы сложной формы. Математик вывел формулы формы и за несколько часов, взяв соответствующие интегралы, получил ответ. И был удивлен, когда Эдисон назвал ему искомую цифру. «Как вы получили этот ответ?», - спросил он. Эдисон молча заполнил колбу водой и вылил воду в мерную мензурку. [Nahin2016p16]

[388] Nahin2016: Paul J. Nahin: In praise of simple physics. The science and mathematics behind everyday questions. - New Jersey: Princeton University Press, 2016. - 241p.

40A. Тугая калитка в доме Эдисона
В доме знаменитого американского изобретателя Томаса Эдисона была весьма необычная входная дверь. Очень-очень тугая. Знакомые Эдисона, заходя к нему в гости, всё время удивлялись и даже возмущались – почему так тяжело открывается входная калитка. Кто-то из друзей сказал ему:
- Такой гений, как ты, Томас, мог бы сконструировать калитку получше.
- А мне кажется, - ответил Эдисон, - калитка сконструирована прекрасно. Она соединена с насосом домашнего водопровода. Каждый, кто приходит ко мне, накачивает в цистерну 20 литров воды.
https://polzam.ru/index.php/istorii/item/1144-zabavnye-istorii-iz-zhizni-tomasa-edisona

41. Вопросы на интервью у Джоэла Сполски (Joel Spolsky): “How many piano tuners are there in Seattle?”
https://www.joelonsoftware.com/2006/10/25/the-guerrilla-guide-to-interviewing-version-30

42. Задача Дидоны. Карфаген и шкура быка. Царица Дидона.
Разрезать шкуру быка на полоски и окружить получившейся веревкой гору Бирсу.

https://ru.wikipedia.org/wiki/Задача_Дидоны

https://commons.wikimedia.org/wiki/Category:Dido#/ media/File:Dido_purchases_Land_for_the_Foundation_of_Carthage.jpg

Шкура крупного рогатого скота 200-500 дм². Нарежем на полоски по 1 см шириной самую крупную шкуру. Получим шнур длиной 500м. Этого мало, так что придется нарезать каждую полоску на 3. Тогда длины шнура хватит. Но с трудом.

http://www.otkani.ru/leathercommodity/skinproperties/2.html

[389] Тихомиров1986: Тихомиров В.М. Рассказы о максимумах и минимумах. - М: Наука, 1986. - 192с. (Библиотечка "Квант"; Выпуск 56).
http://ilib.mccme.ru/djvu/bib-kvant/max.htm

Царица Дидона. [Коваль1972p404]

[390] Коваль1972: Коваль Станислав: От развлечения к знаниям. Математическая смесь.- пер. с польского. - Warszawa: Wydawnictwa naukowo-techniczne, 1972. - 539с.

Перельман2003P190.

43. [391] Carlson2010: Nicholas Carlson: Answers To 15 Google Interview Questions That Will Make You Feel Stupid// Business Insider. Nov 9, 2010, 6:57 PM.
https://www.businessinsider.com/answers-to-15-google-interview-questions-that-will-make-you-feel-stupid-2010-11

44. Задача Маршака о землекопе:
"И вышло у меня в ответе:
Два землекопа и две трети."
http://www.world-art.ru/lyric/lyric.php?id=4253

45. [392] 140Google.2009: 140 Google Interview Questions//Impact Interview. October 24th, 2009.
https://www.impactinterview.com/2009/10/140-google-interview-questions

46. Пойя Дьёрдь(1887-1985):

[393] Пойя2002: Дж.Пойа, Д.Килпатрик Сборник задач по математике Стенфордского университета: с подсказками и решениями. - М: НО Научный фонд «Первая Исследовательская лаборатория им. академика В.А.Мельникова», 2002. - 96с.
Ориг. назв.: G.Polya, J.Kilpatrick: The Stanford Mathematics Problem Book with Hints and Solutions. 1974.

[394] Пойя2010: Дж.Пойа (1887-1985) Математическое открытие. Решение задач. Основные понятия, изучение и преподавание. Пер. с англ. - Изд. 3-е. - М: КомКнига, 2010. - 448с.
Ориг. назв.: George Polya: Mathematical Discovery: On understanding, learning, and teaching problem solving. 1962.

[395] Пойя1975: Дж.Пойа Математика и правдоподобные рассуждения. - Изд. 2-е, испр. - М: Наука, 1975. - 464с.
Ориг. назв.: George Polya: Mathematics and Plausible Reasoning. 1954.

47. Академик Л.А. Арцимович дал следующее определение науки: (журнал «Новый мир», номер 1, 1967):
«Наука есть лучший современный способ удовлетворения любопытства отдельных лиц за счет государства»
http://physics.lyceum1501.ru/fiziki_shutjat.html
{Арцимович Л.А. — Физик нашего времени (Заметки о науке и ее месте в обществе)//Новый мир. 1967. N1. с.190-203.}

#362 48. Какой высоты должна быть башня барона фон Гленна (в наст. время Таллинская обсерватория), чтобы увидеть финский берег? Скажем сразу, что она не была построена до требуемой высоты.

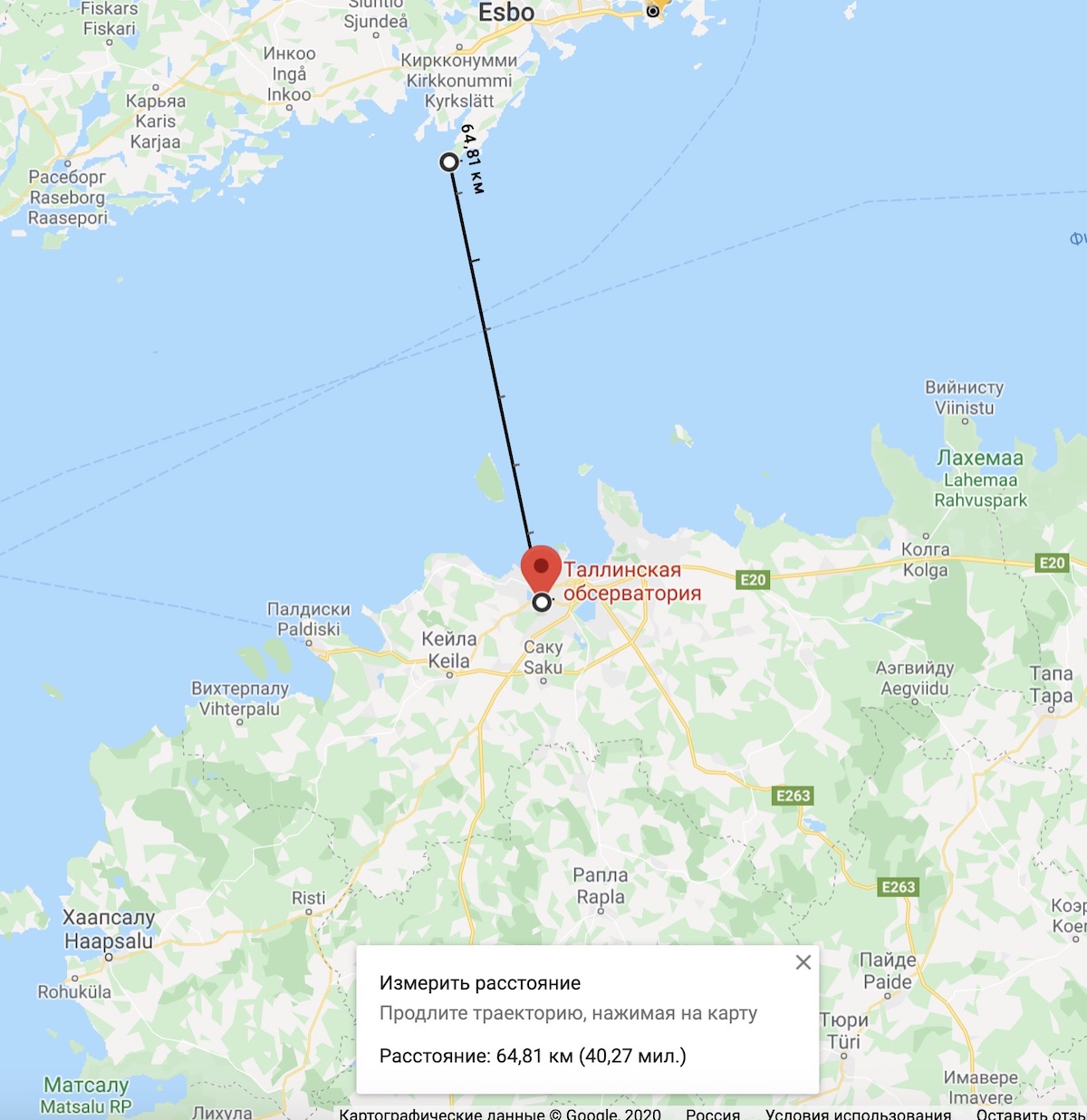
{Google Maps определяют расстояние до ближайшей точки финского берега в 65 км. Следовательно, высота башни должна быть (65/3.6)^2 = 325 м. При этом отсчет ведется от уровня моря.
Как уже отмечалось, башня Гленна требуемой высоты не достигла, хотя и находилась на холме. Однако аэростаты и современные дроны с камерами легко достигают необходимой высоты. Увидеть финский берег таким образом вполне возможно и дело только за погодой и облачностью.
Определение размера Башни Гленна.
Google Maps: 6 см. Масштаб 1.5 см - 2 м. Итого 8м.
Велосипед 2 м - 2см, всего 10 см - 10м
С высотой в 75м, указанной в Wikipedia, есть сомнения. Может быть это от уровня моря?
(P.S. За башню Гленна спасибо Кирикову П.Н.)}

https://ru.wikipedia.org/wiki/Глен,_Николай_фон

https://www.stena.ee/blog/stena_news/ekskursiya-v-tallinskuyu-zvezdnuyu-bashnyu-t%C3%A4hetorn

https://egorov.livejournal.com/327090.html

49. Дьяконов В.П. (1940-2015) Программирование на калькуляторах. Компьютерная математика.
https://ru.wikipedia.org/wiki/Дьяконов,_Владимир_Павлович

[396] Дьяконов1999: Дьяконов В.П. Америка глазами профессора
http://old.exponenta.ru/educat/news/dyakonov/wolfrr/wolfrr.asp

50. [397] Alisher2019: Алишер Кадыркулович (ИВТ Политех): Головоломки (без ответов).2019:
http://students.njay.ru/cooler/puzzles

51. Комета Шумейкеров — Леви 9 (D/1993 F2) 
Comet Shoemaker–Levy 9 (D/1993 F2)
  Открыта 23 марта 1993г. Упала на Юпитер в июле 1994г. Всего 21 фрагмент. Энерговыделение 6 млн.мегатонн THT.
https://ru.wikipedia.org/wiki/D/1993_F2_(Шумейкеров_—_Леви)

52. Венгерская нотация
https://ru.wikipedia.org/wiki/Венгерская_нотация

{Писать слова слитно, начиная каждое с большой буквы, восходит к Венгерской нотации Чарльза Симони, ведущего программиста Микрософт в свое время (MS-DOS, Multiplan, Excel, Word) , который именовал переменные как NewOldValue, а на вопрос что это такое отвечал: это венгерская нотация, поскольку сам и был венгром. Симони также дважды слетал на Международную Космическую Станцию как турист на космическом корабле "Союз ТМА", а свои первые программы писал на ЭВМ "Урал".}
Чарльз Симони (Charles Simonyi)(1948-)
https://ru.wikipedia.org/wiki/Симони,_Чарльз

53. Как по плотности цемента определить размеры величин при строительстве Исакиевского собора.
[Иванова_Суетин2019p136]

[398] Иванова_Суетин2019: Иванова С.А., Суэтин А.Г. Хождение по дебрям информации, или Алгоритмы понимания: Познание в эпоху незнания: самоучитель работы с информацией. - Предисл. Г.Г.Малинецкого. - М: ЛЕНАНД, 2019. - 352с.

54. "ИдиотенТест" для немецких водителей лишенных прав:
Вопрос 66:

Девушка посадила в пруд быстро растущую лилию, которая удваивается каждый день. На второй день уже две лилии было в воде пруда, 4 на третий, восеь на четвертый день и т.д. Через 28 дней пруд был заполнен лилиями. Через сколько дней пруд был наполовину полон водными лилиями.

https://pikabu.ru/story/ idiotentest_dlya_nemetskikh_voditeley_lishennyikh_prav_1443959

55. Профессор Джеймс Мориарти (Антагонист Шерлока Холмса): Динамика астероида. (Cards.html)

56. Парадокс Монти Хилла.
https://ru.wikipedia.org/wiki/Парадокс_Монти_Холла

Загадка про студента и ректора
https://zen.yandex.ru/media/komunalka/zagadka-pro-studenta-i-rektora-5dd6602c26b6164597866afd

{Автор статьи проделывает эксперимент с заменой билетов и подтверждением Парадокса Монти Хилла.}

Парадокс Монти Холла (наглядный пример):
https://zen.yandex.ru/media/komunalka/paradoks-monti-holla-nagliadnyi-primer-5dd92808302888135726bd26

57. Теорминимум для программиста. (Всего 33 пункта)
https://sharpc.livejournal.com/67583.html

11. Численные методы, дихотомия/метод Ньютона, интер- и экстраполяция, сплайны, метод Гаусса/Якоби/Зейделя, QR и LU-декомпозиция, SVD, МНК, методы Рунге-Кутты, метод Адамса, формулы Ньютона-Котеса, метод Ритца, метод Бубнова-Галеркина, метод конечных разностей/элементов, FFT/STFT, сходимость и устойчивость.

58. Задача про 5 станков и 8 рабочих. //М772. New1. Квант. 1983. N2 с.46: 
http://kvant.mccme.ru/1983/02/p46.htm

59. Формула Герона (вывод)
https://interneturok.ru/lesson/geometry/8-klass/ploschad/formula-gerona-dlya-nahozhdeniya-ploschadi-treugolnika

60. Реевский Мариан (Marian Adam Rejewski) (1905-1980). Польский Генеральный штаб. Первым раскрыл код Энигмы. После войны работал в Польше, не афишируя свою деятельность по Энигме до 1973г.
https://ru.wikipedia.org/wiki/Реевский,_Мариан

При расшифровке польский начальник доводил не всю информацию, проверяя таким образом работу дешифровальщиков [Сингх2007p181].

61. [399] Аникеев2010: Аникеев А.А., Иващенко А.Г. (сост.) Военная топография. Учебное пособие. Уссурийск: Кузбасский институт ФСИН России», 2010г. - 102с.

1.3. Определение расстояний при ориентировании на местности и целеуказание
https://scicenter.online/voennaya-topografiya-scicenter/opredelenie-rasstoyaniy-pri-orientirovanii-123568.html

62. Фунты, ярды, пинты и прочие мили в час на английском языке, 23.01.2017
http://ua-contact.com/ru/novosti/135-funty-yardy-pinty-i-prochie-mili-v-chas-na-anglijskom-yazyke

Американские меры температуры, длины и веса. Размеры одежды и обуви.

Единицы измерения в США:
https://nyc-brooklyn.ru/edinici-izmereniya-usa

Перевод англо-американских мер в метрические
https://gazovik-gaz.ru/spravochnik/apps/ediniczyi-velichin/anglo-american-v-metricheskie.html

Таблицы мер и весов
https://www.samru.ru/spravka/trans/23313.html

Единицы измерения по-английски
https://englishfull.ru/znat/edinicy-izmereniya.html

Английская система мер//Wikipedia:
https://ru.wikipedia.org/wiki/Английская_система_мер

Celsius, Fahrenheit, Kelvin: Sundem:The Geeks' Guide to World Domination. 2009,p.74.

63. Русская система мер. Старинные единицы измерения.(Интересный рис.)
http://blog.vilisov.info/article/20

64. Сайт: Империя чисел
https://ru.numberempire.com

65. Фибоначчи.Книга абака.
https://ru.wikipedia.org/wiki/Книга_абака

66. Непер «Описание удивительной таблицы логарифмов» (1614 год)

67. Хитрая математика против Пенсионного фонда
https://chern-molnija.livejournal.com/925585.html

68. Бематисты. Греческие ходоки, измеряющие расстояние шагами. Ходили с армией Александра Македонского в том числе.
https://en.wikipedia.org/wiki/Bematist

69. Елькин В.И. (Переехал в D§130)

70. #363 Направьте стрелку часовую...

Направьте стрелку часовую
На Солнце точку золотую.
Меж стрелкою и цифрой "час"
Есть угол, важен он для нас.
Делите угол пополам
И сразу юг найдете там...
                                           Рос А.

[Артемьев_Забочень1995p40]

[400] Артемьев_Забочень1995: Артемьев В.И., Забочень М.С. Открытки изданные в Москве в годы Великой Отечественной войны, 1941-1945 гг: каталог. - М: Российская гос. библиотека, 1995. - 158с.
books.google.ru

https://pikabu.ru/story/chasyi_kak_kompas_6570649

71. #364 Туристы перешли с одного берега озера, где располагалась их база, на другой и, посмотрев на часы, решили устроить короткий отдых. Стояла тихая погода, и им были хорошо слышны передачи радиоузла базы; поэтому последние известия они смогли прослушать, выключив свой переносный радиоприемник. После этого один из туристов заявил, что расстояние до базы - почти 3 километра. Каким образом он определил это расстояние?
[Елькин:Занимательная физика.2003]

72. Памятки из детства:

Биссектрисса - это крыса.
Крыса ходит по углам, делит угол пополам!

73. [401] Браверман_Мучник1983: Браверман Э.М., Мучник И.Б. Структурные методы обработки эмпирических данных. - М: Наука, 1983. - 464с.
Браверман Эммануил Маркович (1931 — 1977)
https://ru.wikipedia.org/wiki/Браверман,_Эммануил_Маркович
https://www.ipu.ru/node/11933

74. Арьков Валентин Юрьевич. Excel.

75. [402] Чиркова2017: Чиркова Елена Как оценить бизнес по аналогии. Пособие по использованию сравнительных рыночных коэффициентов. - 4-е изд., испр. и доп. - М: Альпина Паблишер, 2017. - 284с.
http://www.elenachirkova.com

[403] Петров_Чиркова2012: Петров И., Чиркова Е. Системы вознаграждения высшего менеджмента компаний на примере акций// "Экономическая политика", 2012, №5
http://www.elenachirkova.com/images/articles/sistemy-voznagrazhdeniya.pdf

76. [404] Reimer2005: Jeremy Reimer: Total share: 30 years of personal computer market share figures. It's been a long, strange trip for the personal computer over 30 years. Ars …// arstechnica.com - 12/15/2005, 8:00 AM
https://arstechnica.com/features/2005/12/total-share

77. 7+9=10 Добавить одно математическое действие, чтобы равенство стало верным (в комментариях):
1. Корень перед 9.
2. 7^0 (семь в нулевой степени).
3. Шестнадцатиричная система.

https://zen.yandex.ru/media/razvivatel/golovolomka-na-logiku-sdelaite-tolko-odno-deistvie-chtoby-ravenstvo-bylo-vernym-smojete-reshit-za-1-minutu-5e82322be76e9e2043c80919

78. [405] Неретин2016: Неретин Юрий: Записки по истории Колмогоровской реформы школьной математики// 17.10.2016
https://mat.univie.ac.at/~neretin/misc/reform/reforma1965.html

Неретин Юрий Александрович (1959-)
http://new.math.msu.su/tffa/persons/neretin.html

79. Ошибка базового процента/ложное срабатывание для анализов (в англ. варианте), алкотестере, камере слежения.
https://ru.wikipedia.org/wiki/Ошибка_базового_процента

80. Оценка смертности и рождаемости в день. Оценка и реальность. 5000.
{Количество смертей в день, нормальное для данной территории определяется исходя из численности населения. Делим численность на средний возраст и на 365. Если грубо, то на 100 (погрешность 39%) и на 300 (погрешность 21%, но в другую сторону).
Россия: Население: 140 млн. чел. В день 4700 чел.
За январь-февраль 2020 умерло 307.3 тыс. чел. - в день (/59): 5208.
Если посчитать более точно:
144.5 млн. чел./72 (средний возраст)/365 = 5498.}
https://www.rbc.ru/rbcfreenews/5e8c5c109a79477a45796baf
[Adam1995p23]
[Paulos200111]

Смертность в России на фоне пандемии стала рекордной за десять лет Прирост умерших превышает прямые потери от COVID-19
https://www.rbc.ru/society/16/12/2020/5fbd65c79a794747f677e904?from=column_2

81. Алгоритм Карацубы:
https://ru.wikipedia.org/wiki/Алгоритм_Карацубы

Карацуба Анатолий Алексеевич (Anatoly Karatsuba) (1937-2008) https://ru.wikipedia.org/wiki/Карацуба,_Анатолий_Алексеевич

82. Абрамочкин Евгений Григорьевич:
http://www.ega-math.narod.ru

83. Scheaffer: Activity-based statistics в §120/128.

84. PlanetMath.org. University of Waterloo Faculty of Mathematics. Canada.
https://planetmath.org

85. Определение крепости хлебного вина методом отжига.
https://ru.wikipedia.org/wiki/Отжиг_хлебного_вина

86. [406] Кейнс2005: Дж. М. Кейнс. "Общая теория занятости, процента и денег" (The General Theory of Employment, Interest and Money, 1936)
http://ek-lit.narod.ru/keynsod.htm

Кейнс Джон Мейнард (John Maynard Keynes)(1883-1946)
https://ru.wikipedia.org/wiki/Кейнс,_Джон_Мейнард

87. Пределы роста. 1972.
https://ru.wikipedia.org/wiki/Пределы_роста

88. Индекс Ли Кэцяна

Li Keqiang index
https://en.wikipedia.org/wiki/Li_Keqiang_index

https://www.vedomosti.ru/economics/articles/2017/05/29/691810-statistika-kitaya

89. «Мышиный помет»: почему США обвинили китайские компании в приписках
https://pro.rbc.ru/demo/5e941ef49a794781d801854b?from=related_materials

{Оценка отчетов китайских компаний
Luckin Coffee - сеть кофеен
iQiyi - стриминговый сервис
индекс Ли Кэцяна}

90. [407] Золотов2012: Золотов Евгений: Короткий век цифры: почему стареют электронные накопители// Компьютерра, 16 мая 2012
https://www.computerra.ru/187049/digital-aging

{Цифровая археология}

91. Старые форматы записей

Жизнь на Марсе есть! С таким оптимистичным заявлением выступил американский нейробиолог Джозеф Миллер (Joseph Miller), тщательно проанализировав информацию, полученную аппаратами Viking 1 и 2, совершившими посадку на Красной планете в 1975 году.

Исследователь добился от руководства NASA полных результатов экспериментов (столкнувшись по пути с неожиданной проблемой: записи хранились на магнитной ленте в формате столь старом, что даже программисты, его придумавшие, уже умерли; к счастью, отыскались распечатки) и, обработав их, обнаружил, что период активности точно соответствует марсианским суткам.

Компьютерра, Новости, 10.08.2001
https://old.computerra.ru/2001/407/197784

[408] DiGregorio2000: Barry E. DiGregorio: Viking Data May Hide New Evidence For Life, July 16, 2000
https://www.spacedaily.com/news/mars-life-00g.html

92. Индекс Хирша
https://ru.wikipedia.org/wiki/Индекс_Хирша

[409] Hirsch2005: J.E. Hirsch: An index to quantify an individual's scientific research output. //Proc.Nat.Acad.Sci.46:16569,2005
DOI:10.1073/pnas.0507655102
Cite as: arXiv:physics/0508025 [physics.soc-ph]
https://arxiv.org/abs/physics/0508025

Хорхе Хирш (англ. Jorge Hirsch)(1953-)
https://ru.wikipedia.org/wiki/Хирш,_Хорхе

93. [410] Ализар2015: Анатолий Ализар: Количество соавторов научных работ всё чаще превышает тысячу человек.//11 августа 2015 в 23:51
https://habr.com/ru/post/382841

{"Французский физик Жорж Аад (Georges Aad) обычно упоминается первым в числе соавторов, если список составляется по алфавиту" (G. Aad et al.)}

[411] Hotz2015: Robert Lee Hotz: How Many Scientists Does It Take to Write a Paper? Apparently, Thousands Scientific journals see a spike in number of contributors; 24 pages of alphabetized co-authors// The Wall Street Journal, Aug. 10, 2015 4:04 pm ET
https://www.wsj.com/articles/how-many-scientists-does-it-take-to-write-a-paper-apparently-thousands-1439169200

94. [412] Бронштейн_Семендяев1957: Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. - Изд. седьмое, стереотип. - М: Государственное издательство технико-теоретической литературы, 1957. - 608с.
http://publ.lib.ru/ARCHIVES/B/BRONSHTEYN_Il'ya_Nikolaevich/_Bronshteyn_I.N..html

Издание 1957: с.562 Раздел 6. Обработка наблюдений.

Справочник_по_математике_(Бронштейн,_Семендяев)
https://ru.wikipedia.org/wiki/Справочник_по_математике_(Бронштейн,_Семендяев)

Бронштейн Илья Николаевич (1903—1976)
https://ru.wikipedia.org/wiki/Бронштейн,_Илья_Николаевич

Семендяев Константин Адольфович (1908 — 1988)
https://ru.wikipedia.org/wiki/Семендяев,_Константин_Адольфович

95. Метод звёздных черпков Гершеля (Herschel's star-‐gage method)
https://ru.wikipedia.org/wiki/Метод_звёздных_подсчётов

Гершель Уильям (англ. Frederick William Herschel)(1738 — 1822)
https://ru.wikipedia.org/wiki/Гершель,_Уильям

96. Численные методы

[413] Волков1987.BC: Волков Е.А. Численные методы: Учеб. пособие для вузов.-2-е изд., испр. — М: Наука, 1987. — 248 с.

Волков Евгений Алексеевич (1926-2019)
https://ru.wikipedia.org/wiki/Волков,_Евгений_Алексеевич

[414] Бахвалов2008: Бахвалов Н.С. , Жидков Н.П., Кобельков Г.М. . Численные методы. — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008. — 636 с.
http://publ.lib.ru/ARCHIVES/B/BAHVALOV_Nikolay_Sergeevich/_Bahvalov_N.S..html

Бахвалов, Николай Сергеевич (1934-2005)
https://ru.wikipedia.org/wiki/Бахвалов,_Николай_Сергеевич

[415] Зенков1997.BC: Зенков, А.В. Численные методы: учеб. пособие. — Екатеринбург : Изд- во Урал. ун-та, 2016. — 124 с.

Зенков Андрей Вячеславович: Уральский федеральный университет.
http://sei.usue.ru/prepodavateli/350-zenkov-andrej-vyacheslavovich

[416] Митин_Русаков1998.BC: Митин И.В., Русаков В.С. Анализ и обработка экспериментальных данных : [учеб.-метод. пособие для студентов мл. курсов]. - 2-е изд., испр. - М. : Изд-во НЭВЦ ФИПТ, 1998. - 43 с. Библиогр. с.48 (8 назв.)

[417] Березин_Жидков1962.BC: Березин И.С., Жидков Н.П. Методы вычислений. — М.: Наука, 1962. — Т. 1., Т.2(1959).

Березин Иван Семёнович (1920-1982)
https://ru.wikipedia.org/wiki/Березин,_Иван_Семёнович

Жидков Николай Петрович (1918-1993)
https://ru.wikipedia.org/wiki/Жидков,_Николай_Петрович

[418] Калиткин1978.BC: Калиткин Н.Н. Численные методы. - М: Наукаб 1978. - 512с.

Калиткин Николай Николаевич (1935-)
https://ru.wikipedia.org/wiki/Калиткин,_Николай_Николаевич

[419] Рыжиков2007: Рыжиков Ю. Вычислительные методы. — СПб.: BHV, 2007. — 400 с.

[420] Амосов1994: Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. - М: Высшая школа, 1994. - 544с.

97. Hutte

Hutte: Справочник для инженеров, техников и студентов.
http://publ.lib.ru/ARCHIVES/H/%27%27Hutte%27%27/_%27%27Hutte%27%27.html

Хютте: Справочник для инженеров, техников и студентов.
https://ru.wikipedia.org/wiki/Хютте

Математика и статистика
(проф. П. Руге, строительная механика и строительная информатика, ТУ Дрезден. Проф. М. Вермут, дорожное и городское машиностроение, ТУ Брауншвейг) величины, логика, графики, изображения, последовательности, матрицы, тензоры, геометрия, проекции, Функции, дифференцирование, интегрирование, конформное отображение, ряды Фурье, полиномиальные развития, интегральные преобразования, дифференциальные уравнения, расчет вариаций, матричные задачи на собственные значения, интерполяция, численное интегрирование, расчет вероятностей, распределение случайных величин и вероятностей, статистика, методы статистических тестов, регрессия.

https://web.archive.org/web/20070505092752/http://www.av-huette.de/93.html
Перевод Google.

98. [421] Выгодский1977: Выгодский М.Я. Справочник по высшей математике. - М: Наука, 1977.

[422] Выгодский1987: Выгодский М.Я. Справочник по элементарной математике. - Издание 27-е, исправленное. - М: Наука, 1987.

Выгодский Марк Яковлевич (1898-1965)
http://publ.lib.ru/ARCHIVES/V/VYGODSKIY_Mark_Yakovlevich/_Vygodskiy_M.Ya..html

https://ru.wikipedia.org/wiki/Выгодский,_Марк_Яковлевич

99. Алиса и Боб бегут марафон.

Алиса бежит равномерно, а Боб резко ускоряясь в начале каждой мили, а в конце прибегает на 1 с. позже Алисы. Может ли Боб пробежать марафон (42 км) быстрее Алисы?

[Landsburg2018]

[423] Landsburg2018: Steven Lansburg: Can You Outsmart an Economist?: 100+ Puzzles to Train Your Brain. - Boston, New York: Mariner Books, 2018. - 304p. (Kindle).

100. [424] Тейлор1985: Тейлор Дж. Введение в теорию ошибок. - Пер. с англ. - М: Мир, 1985. - 272с.
Ориг. назв.: John R. Taylor: The Study of Uncertainties in Physical Measurements.

101. Квайн (quine) - программа печатает свой код
https://ru.wikipedia.org/wiki/Куайн_(программирование)

Названы в честь Уиллард Ван Орман Куайн (англ. Willard Van Orman Quine)(1908-2000)
https://ru.wikipedia.org/wiki/Куайн,_Уиллард_Ван_Орман

Quine на Python
https://tirinox.ru/quine-in-python

Python: s='s=%r;print(s%%s)';print(s%s)

Программа, печатающая собственный исходный текст. [Уэзерелл1982p59]

102. Теорема о бесконечных обезьянах, которые печатают произведения Шекспира на пишушей машинке.
https://ru.wikipedia.org/wiki/Теорема_о_бесконечных_обезьянах

103. [425] Уэзерелл1982: Уэзерелл Ч. Этюды для программистов. Пер. с англ. М. Мир 1982. - 288с.
http://publ.lib.ru/ARCHIVES/U/UEZERELL_Charl'z/_Uezerell_Ch..html

Программа, печатающая собственный исходный текст.
[Уэзерелл1982p59]

Моделирование движения на автостраде.
[Уэзерелл1982p95]

104. [426] Ferriss2009: Tim Ferriss: Scientific Speed Reading: How to Read 300% Faster in 20 Minutes
https://tim.blog/2009/07/30/speed-reading-and-accelerated-learning

Средняя скорость чтения 120-180 слов/мин. на русском
США: средняя скорость чтения 200-300 слов/мин.
От 1/2 до 1 с. в мин.

105. [427] Крамаренко2007.BC:
Энциклопедия Инструмента. Том 1. “МЕРИТЕЛЬ. ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ”. - Пятое переработанное и дополненное издание//Крамаренко Б.П., Гревцова Т.Е., Крамаренко С.Б., Млечин А.И., Иогансон Н.И., Злобина Т.Е - Харьков: МИКРОТЕХ®, 2007г. - 228с.

106. [428] Cliborn2011: Jim Cliborn: Fermi Problems, Introduction//Jim Cliborn's Garden of STEMs (STEMs--Science, Technology, Engineering and Mathematics, a technical notebook),November 12, 2011:
http://jimclibornsnotebook.blogspot.com/2011/11/fermi-problems-introduction.html

107. [429] Sachs2015: Jason Sachs: Margin Call: Fermi Problems, Highway Horrors, Black Swans, and Why You Should Worry About When You Should Worry// December 6, 2015
https://www.embeddedrelated.com/showarticle/888.php

108. Сколько волос на голове?
{Примерно 150 тысяч. В день мужчины теряют 120, а женщины - 80.
Конечно, вы, добрый читатель, вправе спросить: а зачем нам вообще измерять количество волос на голове?
Не скажите, те методы, которые мы используем, легко могут быть перенесены на другие объекты. Например, можно считать количество волос в бороде. А это может быть очень важной информацией: должен же Старик Хотабыч знать количество исполнимых желаний.}

109. Как проверить, что до Солнца 150 млн. км.
Рихер и Кассини. По орбите Марса.1672.
https://spacegid.com/kakovo-rasstoyanie-do-nashego-svetila.html

[430] Добронравин1938: Добронравин П.П. Измерение расстояний в мировом пространстве// Наука и жизнь. N6. 1938. c.12-16

Скорость Земли по орбите 30 км/с и расчет расстояния до Солнца.
Умножаем на количество секунд в году и делим на 2*Pi:
30*365*24*60*60/(2*3.14) = 150.6 млн.км.
{Вопрос только в том, откуда мы знаем скорость движения Земли по орбите.}

Как найти расстояние до звезд?
[431] Добронравин1938: Добронравин П. П. Измерение расстояний в мировом пространстве. Расстояния звезд.//Наука и жизнь. 1938. N9. с.28-33.
https://www.nkj.ru/archive/articles/32209

110. [432] Шаврина2017: Шаврина Т.О. Методы обнаружения и исправления опечаток: исторический обзор. //Вопросы языкознания. 2017. N4. С.115-134. Библиогр.с.131-134. (61 назв.)
https://publications.hse.ru/mirror/pubs/share/direct/209127143

{Татьяна Олеговна Шаврина (Национальный исследовательский университет "Высшая школа экономики")}

111. Вы баскетболист. Вероятность успешного броска p.
Что лучше 1 бросок из 1.
2 из 3.
1 из 2. (вторая попытка)
3 из 5.
[Паундстоун2012p252-256.]
[Макдауэлл2016p299-300.]

112. Вопрос на военной кафедре: торпеда попадает в цель с вероятностью 80 процентов. С какой вероятностью поразят цель две торпеды. (80+80?).
Правильный ответ: 1-0.2*0.2=0.96
Считается, что достаточно попадания одной торпеды (из двух запущенных)

113. Вы едете со скоростью 100 км/ч из пункта А в пункт В и со скоростью 50 км/ч обратно. Какой была средняя скорость?
https://baguzin.ru/wp/mentalnye-lovushki/

{Средняя скорость равна удвоенному расстоянию деленному на время езды с каждой скоростью:
2s/(s/100+s/50), s сокращаются.
Ответ: 66.6 км/ч}

114. Как определить глубину пруда по кувшинкам. А глубину моря по разрушенным нефтяным вышкам.
[Перельман2014p217].

[433] Перельман2014: Перельман Я.И. Большой подарок эрудиту. Что? Зачем? Почему? Занимательная физика, механика, астрономия, математика, природа. - М: АСТ, 2014. - 240с.

[434] Горяев2015: Горяев В.М. Задача о лотосе в курсе математики// Международный журнал экспериментального образования. – 2015. – № 2 (часть 1) – С. 61-62.
https://www.expeducation.ru/ru/article/view?id=6425

115. Простые числа до 100.
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,59,61,67,71,73,79,83,89,97]
[Ташнер2018p104]

116. Защита атомной станции от самолета:
http://engine.aviaport.ru/issues/109/pics/pg24.pdf

117. Росстат измерил «невидимую» экономику России
https://www.rbc.ru/economics/29/08/2019/5d651ed89a79474a0d725030

118. Сколько человек пришло на митинг за Лукашенко и акцию у Cтеллы: считаем по фото с высоты.(16 августа 2020 в 16:52)
https://42.tut.by/696889?tg

119.

I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of Science, whatever the matter may be.
Lord Kelvin, 1883

Я часто говорю, что если вы можете измерить то, о чем вы говорите, и выразить это в числах, тогда вы что-то об этом знаете. Но если вы не можете измерить это, не можете выразить в числах, тогда ваши познания скудны и неудовлетворительны. Это могут быть начальные знания, но едва ли вы в своих мыслях продвинулись до состояния науки.

https://atmos.uw.edu/~robwood/teaching/451/Lord_Kelvin_quote.pdf

Томсон, Уильям (лорд Кельвин) (William Thomson, 1st Baron Kelvin)(1824-1907)
https://ru.wikipedia.org/wiki/Томсон,_Уильям_(лорд_Кельвин)

120. Статистика - это наука, она не терпит приблизительности.
Калугина Людмила Прокофьевна. (к/ф Служебный роман).
https://www.youtube.com/watch?v=SeC25LIPay4

121. Самая популярная и непростая задачка от английского учителя геометрии.
https://zen.yandex.ru/media/infoniac.ru/samaia-populiarnaia-i-neprostaia-zadachka-ot-angliiskogo-uchitelia-geometrii-5f3e98b0a79c120efb53a3e7
Через координаты касания квадратов с окружностью определить радиус. Соединить точки касания отрезками. Построить перпендикуляр в середине каждого отрезка. Точка пересечения этих перпендикуляров будет центром окружности.

122. Самая сложная из простых задач теста для поступления в высшие учебные заведения США, и решить её нужно за 1-2 минуты
https://zen.yandex.ru/media/infoniac.ru/samaia-slojnaia-iz-prostyh-zadach-testa-dlia-postupleniia-v-vysshie-uchebnye-zavedeniia-ssha-i-reshit-ee-nujno-za-12-minuty-5f514bfd4330f118aa278cce
https://www.infoniac.ru

123. Парадокс Паррондо (Комбинация проигрышных стратегий, которые выигрывают)
Паррондо Хуан (исп. Juan Manuel Rodríguez Parrondo)(1964-) (Испанский физик, Мадридском университете Комплутенсе)
https://ru.wikipedia.org/wiki/Паррондо,_Хуан
https://ru.wikipedia.org/wiki/Парадокс_Паррондо

124. [435] Eastaway2013: Rob Eastarway: Zequals and Estimation - Numberphile
https://www.youtube.com/watch?v=aOJOfh2_4PE

125. [436] Mclvor2018: Nick McIvor: 4. Estimation - Fermi Estimation: How to carry out order of magnitude estimations based on very rough estimates for values.
Как оценить порядок величины на основе грубых оценок.
https://www.youtube.com/watch?v=9TmymicajXs
How many pupils are there in the UK school system? (6:04)
Сколько человек учится в британских школах?

126. Ферми и аспирант.

Аспирант приходит к Роберту Оппенгеймеру с задачей, которую не смог решить. Тот ему в течение двух часов читает блестящую лекцию, из которой аспирант понимает очень мало, но уходит в восторге, что есть среди нас гении, способные решать задачи, недоступные простым смертным. Затем он обращается к Швингеру, который за час решает задачу и к тому же так, что аспирант понимает решение. Он уходит в восторге, что есть среди нас такие гении, которые могут сделать столь трудные задачи доступными для простых смертных. Наконец он заходит к Ферми и выходит через пять минут в плохом настроении, страшно недовольный собой, что не сумел сам решить столь простую задачу.

[Абрагам1991p228]

[437] Абрагам.ВремяВспять.1991: Абрагам Анатоль: Время вспять, или физик, физик, где ты был.- Пер. с франц. - М: Наука, 1991. - 392с.
Ориг. назв.: De la physique avant tout chose. 1987. Перевод с франц. А.Абрагама.
http://sovams.narod.ru/Library/abragam.html

Анекдот рассказал: Рамзей, Норман Фостер (Norman Foster Ramsey)(1915-2011)
https://ru.wikipedia.org/wiki/Рамзей,_Норман_Фостер

Швингер Джулиан (Julian Seymour Schwinger)(1918-1994)
https://ru.wikipedia.org/wiki/Швингер,_Джулиан

Стовпюк М. Ф. Попытка определения соционического типа Энрико Ферми. - Динамическая соционика
http://www.dynamicsocionics.ru/stati/drugie-avtory/62-stati/stovpyuk-m/255-stovpyuk-m-popytka-opredeleniya-sotsionicheskogo-tipa-enriko-fermi.html

127. Аспирин снижает госпитальную летальность от СОVID? Обнадёживает, но пока не доказано...
https://prof-afv.livejournal.com/47964.html?utm_source=newsletter&utm_medium=email&utm_campaign=26_10_2020_Monday&media
Chow, Jonathan H. MD and others:
Aspirin Use is Associated with Decreased Mechanical Ventilation, ICU Admission, and In-Hospital Mortality in Hospitalized Patients with COVID-19
https://journals.lww.com/anesthesia-analgesia/Abstract/9000/Aspirin_Use_is_Associated_with_Decreased.95423.aspx

128. Всемирный банк нашел связь между ремонтом дорог и голосами за Собянина.

129. Индекс массы тела. Вес (кг) разделить на рост в квадрате (м). Если рост в см, не забудьте умножить на 10тыс. Введен Адольфом Кетле (Lambert-Adolph-Jacques Quetelet)(1796-1874)
https://www.msdmanuals.com/medical-calculators/BodyMassIndex-ru.htm

Индекс излишнего веса [Скиена2020p136-139]

Индекс массы тела. [Пейдж2020p65-66]

Индекс Кетле. Индекс массы тела. Вес здорового человека пропорционален квадрату роста. Индекс Рорера (к кубу роста). [Уэст2018p70]

Индекс массы тела (Body mass index):
https://ru.wikipedia.org/wiki/Индекс_массы_тела
https://en.wikipedia.org/wiki/Body_mass_index

130. У вас взяли какой-либо анализ. Теперь лаборатория делит его на две части. Первую часть смешивают с 10 другими анализами и с помощью 1 исследования получают результат. Если результат отрицательный, то всем присваивают отрицательный. Если положительный, то берут вторую часть анализа и делают 10 исследований. Если из 100 образцов один положительный, то за 19 (вместо 100) исследований всем присвоят результат (99 отрицательных и 1 положительный).

131. Нестандартный тест по математике. Вам понравится.
https://zen.yandex.ru/media/mathematic/nestandartnyi-test-po-matematike-vam-ponravitsia-5f5133024330f118aa01901b

Интересны 3 задачи:

Пусть имеется 100 кг картофеля, имеющего 99 процентов воды по массе. Картофель просушивают и получают 98% процентов воды. Какая теперь масса картофеля?

Какая цифра чаще всего встречается в статистике на первой позиции?

Вас диагностируют на наличие некоторого заболевания, которое имеется у 1 процента ваших ровесников. Тест, который Вам делают, дает верные результаты в 95 процентах случаев. Какова вероятность Вашей болезни, если Ваш тест положительный?

132. Архимед исследует корону и определяет, что она не из чистого золота. [Ташнер2018p59-60]

Архимед взвешивает корону. [Паундстоун2013:191]

Архимед и корона. [Дэвенпорт2014p134-138]

132A. Архимед и солнечные зайчики.

Массачусетские архимеды сожгли триеру римлян светом Солнца
Леонид Попов, 17 октября 2005
http://web.archive.org/web/20200811195254/http://www.membrana.ru/particle/473

Archimedes Death Ray: October, 2005.
http://web.mit.edu/2.009/www/experiments/deathray/10_ArchimedesResult.html

133. Ориентирование: 3 классных способа, чтобы узнать высоту объекта, не забираясь на него (фото-примеры)
https://zen.yandex.ru/media/building_for_myself/orientirovanie-3-klassnyh-sposoba-chtoby-uznat-vysotu-obekta-ne-zabiraias-na-nego-fotoprimery-5f7feed5bd4c4645569808c0

134. Старый плотник научил, как с помощью "жёлтого" угольника - быстро размечать любые углы: 10°, 20°, 30°, 40° и т.д.
https://zen.yandex.ru/media/building_for_myself/staryi-plotnik-nauchil-kak-s-pomosciu-jeltogo-ugolnika-bystro-razmechat-liubye-ugly-10-20-30-40-i-td-5f882791f12cd832da68f0e2

135. Сколько в среднем надо бросать кость до появления шестерки?
[Мостеллер1971p8]

{Ответ 6 может не так и очевиден, но если вы будете ставить фишку на поле в рулетку и ждать выигрыша в 35 фишек, то в среднем вы поставите 37(36 полей плюс зеро) раз как минимум, иначе казино бы разорилось.}

136. Переформулирование задачи.
Значки в коробках переходят в лампочки, лампочки в таблицы, а таблицы в десятичные числа.
[Фридман_Турецкий1989p73-74]

137. Популярность цветов автомобилей

https://newsroom.axalta.com/2020-12-14-Axalta-continues-automotive-color-leadership-with-68th-Global-Automotive-Color-Popularity-Report#assets_all

138. Математическая ошибка в Арбитраже. Налоговые обязательства не вычли из стоимости компании, а прибавили.
https://www.rbc.ru/finances/08/12/2020/5fcdf7bb9a7947dff5f33c84?from=from_main_2
Но вроде исправились.
https://www.rbc.ru/finances/02/03/2021/603e544b9a7947617fad1a6c

139. Соотношение количества бигмаков в медианой зарплате на руки в России и США
https://genby.livejournal.com/885030.html

Стоимость Биг Мака в России за 30 лет. 1990-2020
https://genby.livejournal.com/848497.html

The Big Mac index, 21.07.2021
https://www.economist.com/big-mac-index

140.Мультипликаторы.
https://journal.tinkoff.ru/multilplicator
https://smart-lab.ru

141. {Откуда берутся числа и могут ли они быть такими. Как они соотносятся с нашими знаниями о мире.}

142. Зарубежная литература по занимательной математике
https://www.diary.ru/~eek/~eek/p184884113.htm?oam&rfrom=27540

143.Массметр
https://ru.wikipedia.org/wiki/Измеритель_массы_тела_в_невесомости

144. "Это слон, а это нет". Искусственный интеллект учат считать животных со спутника.
https://www.bbc.com/russian/news-55750006

145. Калькулятор
https://poschitat.online

146. Описание геодезических приборов.
[Никитин1967]

147. Расчет накоплений на пенсию.
https://a-nalgin.livejournal.com/2002173.html

148. К апельсину и мякоти. Куб 10*10*10 маленьких кубиков. Сколько кубиков во внешнем слое?
htps://mathreshka.medium.com/куб-10х10х10-41-860a11a5859c
Мы решаем по простому в лоб: 2*10+8*9*4=488. А можно: 10^3-8^3= 488. Результат тот же, зато покрасивее.

Перельман Я.И. рассматривает мякоть вишни:

Во сколько раз объем мясистой части вишни больше объема косточки? Толщину слоя мякоти принять равной ширине косточки.

149. Угол между стрелками часов в четверть четвертого.
https://mathreshka.medium.com/решение-1515-60-dc3f64835126

150. Даниил Хармс "17 лошадей", журнал «Ёж», (№8, 1928)
https://peskarlib.ru/d-harms/17-loshadey/
https://mathreshka.medium.com/17-horses-69-a32c6c6127d4
Особенно нравится идея взять лошадь взаймы у соседа, а потом вернуть.

151. Кипрская гравитационная аномалия
https://prokipr.ru/PAPHOS/anomalnaya-zona-kipra.html

Магнитная гора в Калифорнии. [Перельман1935p61-62]

152. Большие данные
https://trends.rbc.ru/trends/innovation/5d6c020b9a7947a740fea65c

153. Определить место загрузки файла на youtube.com по его размеру.
[Netflix_Черное зеркало_Национальный гимн.]

154. Как оценить доходы соседа.
Сколько вы бы хотели зарабатывать?
Столько, сколько я получаю по мнению моих соседей.

155. Peter Coy: ‘Big’ Data Can Be 99.98% Smaller Than It Appears

156. Система быстрого счёта по Трахтенбергу
https://ru.wikipedia.org/wiki/Система_Трахтенберга

157. [438] Попов2019: Попов С.Б.: Все формулы мира. Как математика объясняет законы природы. - М: Альпина нон-фикшн, 2019. - 288с.
[Попов2019p241] Падение тела.
[Попов2019p246] Высота гор и форма астероидов.

158. Сортируемые отходы в слонах.

Ежегодно в России сортируется 20 млн т твердых коммунальных отходов, этот объем эквивалентен весу 3 млн слонов, заявил генеральный директор Российского экологического оператора (РЭО) Денис Буцаев, выступая на Невском международном экологическом конгрессе.

«В России в настоящий момент сортируется 20 млн т твердых коммунальных отходов из 60 млн т в год, которые образуются. Если представить себе, сколько это в слонах, то это 3 млн слонов», — сообщил Буцаев.

159. "Калькулятор не поможет!" — задача из обычного учебника алгебры, которая ставит в тупик всех учеников. Неравенство Бернулли. Но можно и без него.

[439] Колмогоров2021: Алгебра и начала математического анализа: 10-11 классы: учебное пособие для общеобразоват. организаций / А.Н. Колмогоров, А.М. Абрамов, Ю.П.Дудницын и др.; Под ред. А. Н. Колмогорова. – 29-е изд. – М.: Просвещение, 1987. – 384 с.

Глава 6. Задачи повышенной трудности. №63, в) Сравните числа: 2^(3^100) и 3^(2^150).

[440] Volkov2021: Valery Volkov: Калькулятор не поможет ★ Жесть от Колмогорова ★ Что больше 2^3^100 или 3^2^150 ★ Сравните числа
https://www.youtube.com/watch?v=ckEQ5HojpTE

§154.

Список источников

[441] Barbour1995: John Barbour: Enrico Fermi's Daughter Has Clear Memory of Atomic Age's Dawning : Science: Nella Fermi shared with her physicist father the conviction that the deadly bomb was an inevitable outcome of learning about the atom. //Los Angeles Times January 8,1995
https://www.latimes.com/archives/la-xpm-1995-01-08-mn-17488-story.html

[442] Кикоин2011: Кикоин Константин: По обе стороны свободы. Эссе, очерки, воспоминания. - Иерусалим: Филобиблон, 2011. - 238с.
ON EITHER SIDE OF FREEDOM (Essays, recollections) (Jerusalem: «Philobiblon», 2011)
https://imwerden.de/pdf/kikoin_po_obe_storony_svobody_2011.pdf

[443] Fermi1939: Fermi. Declaration of Intention.
National Archives: http://research.archives.gov/description/281852

[444] Cronin2004: Fermi Remembered. Edited by Cronin, James W. - Chicago, London: The University of Chicago Press, 2004. - 288p.
Table of Contents:
http://catdir.loc.gov/catdir/toc/ecip049/2003020524.html

[445] Сегре1973.C6: Сегре Э. Энрико Ферми. Физик. - М.: Мир, 1973.- 328с.
Эмилио Сегре (итал. Emilio Segrè)(1905-1989), НПФ-1959.
https://ru.wikipedia.org/wiki/Сегре,_Эмилио_Джино

[446] Segre2016.C6: Segrè Gino, Bettina Hoerlin: The Pope of Physics: Enrico Fermi and the Birth of the Atomic Age. - New York: Henry Holt and Company, 2016. - 354p.

[447] Schwartz2017: Schwartz, David N. (1956-) The Last Man Who Knew Everything: The Life and Times of Enrico Fermi, Father of the Nuclear Age. - New York: Basic Books, 2017.

Fermi Problems, p.37-38,66.

[448] Ферми1971: Ферми Э. Научные труды. — В 2-х т. — М.: Наука, 1971—1972.

[449] Амидей1958: Письмо инженера Адольфо Амидея (Adolfo Amidei), профессору Э. Сегре (25 ноября 1958г., Ливорно)
https://biography.wikireading.ru/289589

Краткий список рисунков.(в отдельном окне)

Краткий список задач Ферми.(в отдельном окне)

23.07.2021 07:46

Первая версия: 06.07.2017